地震数据采集系统中的数据压缩与FPGA 实现

李可寒 ，杨俊峰 ，宋克柱

（1.中国科学技术大学核探测与核电子学国家重点实验室，合肥，230026；2.中国科学技术大学近代物理系，合肥，230026）

引 言

地震勘探是当前油气勘探中一种应用广泛的方法[1]，它对数据采集系统的要求有多通道、高精度、数据量大和实时处理等[2]。数据采集系统在采集到地震数据之后，将采集的数据汇聚至控制与纪录模块供以后数据分析使用。基于地震勘探数据采集系统的实时、多通道等要求，数据采集系统需要实时采集和传输大量数据。

在已有的地震数据采集系统中，通常使用拖缆中长度为100 m 的传输线进行数据传输。由于传输距离较长，如果传输速率过快将导致误码率增高。因此，在传输线质量无法提升的情况下，可以使用数据压缩来降低需要的传输速率，从而降低数据传输的误码率，同时也能降低系统的功耗。

现有的地震数据压缩算法[3-4]利用地震波的物理特征采用小波变换、Dreamlet 变换等方式能够起到很好的压缩效果。但这些算法的计算过程较复杂，而且需要输入整个地震数据文件才能完成压缩，很难用于基于现场可编程门阵列（Field programmable gate array,FPGA）的实时采集处理系统，因此需要一种针对地震数据流的压缩算法。

现有的地震数据流压缩算法[5]是一种针对数据流的无损压缩算法，根据地震数据的数值将3 字节的数据压缩至1～4 字节，是一种熵编码。

本文考虑地震波的物理特征，同时使用熵编码，实现了一种针对地震数据流的无损压缩算法。

1 系统简介

海上地震数据采集系统[6-7]分为水下部分和水上部分。水下部分包括采集和传输数据的拖缆，系统可以有多条拖缆；水上部分包括数据处理机箱和室内控制显示工作站，数据处理机箱负责转发控制命令和汇总拖缆数据。由于水下部分的传输距离更长，因此数据传输的瓶颈主要在水下部分。

地震数据采集系统支持若干条拖缆，其中单条水下拖缆的结构如图1 所示。每段拖缆长100 m，里面包含16 个传感器，道间距为6.25 m，采用24 位的ADC，最大采样率为2 ksps，最大要求支持150 段拖缆。两段拖缆之间由传输节点相连，每一个传输节点除了负责收集本级采集数据和状态数据外，还负责接收后级传输节点数据并转发。根据系统结构，越往前级数据量越大，其中满负荷情况下首节点的净数据量可以达到150×16×24×2 000=115.2 (Mb/s)。如果考虑协议开销，首节点需要的传输速率则会更大。

图1 水下拖缆整体结构Fig.1 Integral structure of underwater towline

2 数据压缩

当拖缆段数增加时，首节点需要更大的传输速率。为了控制误码率，可以考虑对地震数据进行压缩，减少需要传输的数据量。另外，传输速率的减小能够降低单个节点的功耗，从而使系统能够支持更多段拖缆。

现有的大部分地震数据压缩算法针对的是一个地震数据文件，用于减小地震数据占用的存储空间，无法在数据采集的时候使用以提高传输效率。现有的地震数据流压缩算法[5]针对的是单个地震数据，利用地震数据的分布特征，将3 字节的地震数据压缩至1～4 字节。该算法没有考虑数据之间的相关性，故而压缩性能有待提升。

本文将根据地震数据的时空特征，同时借鉴语音压缩算法，提出一种易于用FPGA 实现的24 位地震数据流无损压缩算法。

2.1 地震数据

任意两段拖缆之间由一个传输节点相连，每个传输节点负责收集附近16 个传感器采集到的地震数据。为了提高压缩效果，传输节点通常需要缓存若干个采样时刻的数据。图2 为随机截取的连续16 个通道、16 个采样时刻的地震数据，即为待压缩的数据。

从图2 可以看出，待压缩的16×16 地震数据具有如下特点：(1)传感器的数值随采样时刻的变化不大；(2)传感器的数值随传感器号的变化不可预知。

图2 地震数据Fig.2 Seismic data

传感器收集的是地震波数据，地震波本质上是机械波，理想情况下应该是一个类正弦波信号。激发人工地震波的震源频率约为几十赫兹，而传感器的采样周期通常为毫秒量级（对应频率为千赫兹量级），即采样频率远大于振动频率。因此，在不长的时间里，某一个传感器的数值不会有太大的变化。而在同一时刻，相邻传感器采集的数据可能相近，也可能相差很大，这取决于地层结构。由于地层结构无法预知，所以很难事先得知同时刻不同传感器数据之间的关系。

因此，本文中的压缩主要考虑针对同一个传感器在若干个采样时刻的地震数据，这样的数据类似于机械波（声波），故可以借鉴语音压缩的相关算法。

2.2 压缩算法

对地震数据的压缩可以借鉴语音压缩，一种常见的语音压缩算法分为预测编码和熵编码两步，其过程如图3 所示。

图3 语音压缩过程Fig.3 Process of speech compression

2.3 预测编码

预测编码是根据离散信号之间存在着一定关联性的特点，利用前一个或多个信号预测下一个信号，然后对实际值和预测值的差（预测误差）进行编码。如果预测比较准确，误差就会很小。在同等精度要求的条件下，就可以用比较少的比特进行编码，达到压缩数据的目的。

常见的预测编码有线性预测编码，即现在值可用若干个过去值的加权线性组合来逼近，加权系数即为预测系数，预测值为

为使线性预测误差

最小，可以根据实际采样值让线性预测误差的平方达到最小值，从而确定最佳预测系数。

由于线性预测编码比较复杂，尤其是预测系数的计算在硬件上实现起来难度很大，因此考虑一种更加简单的线性预测编码，即差分编码。

对于原始数据X1,X2,…,Xn，一阶差分编码为X1,X2-X1,…,Xn-Xn-1，一阶差分编码是预测阶数p=1，预测系数A1=1 的线性预测编码。预测值=Xn-1，即估计后一个数据和前一个数据差不多。

二阶差分编码为X1,X2-X1,X3-2X2+X1,…,Xn-2Xn-1+Xn-2，二阶差分编码是预测阶数p=2，预测系数A1=2，A2=-1 的线性预测编码。预测值=2Xn-1-Xn-2，即用前两个点拟合一次函数，并预测下一个点会出现在该直线上。

以此类推，可得高阶差分编码。

差分编码只需要作若干次减法，易于硬件上的实现。

2.4 熵编码

由于地震数据及其各阶导数随时间的变化不是很明显，因此地震数据在差分编码之后，其绝对值将变得很小（相比原来的数据）。现在就要想办法用较少的比特来存储这些绝对值很小的数据。

熵编码又称为统计编码，是根据消息出现概率的分布特性而进行的无损数据压缩编码（差分编码之后，绝对值小的数据出现的概率更大）。

2.4.1 指数哥伦布编码［8］

指数哥伦布编码删去了数据高位多余的0（负数删去多余的1），并添加上若干位的标记位。表示非负整数N的k阶指数哥伦布编码生成方法如下：

(1)将N用二进制码表示，去掉低位的k个比特，然后加1；

(2)计算留下的比特数，将此数减1，并记作m；

(3)将第(1)步中去掉的k个比特补回串尾，并在串头添加m个0。

例如，对1 阶指数哥伦布编码，0 到13 的编码如下：

0——0000——10

1——0001——11

2——0010——0100

3——0011——0101

4——0100——0110

5——0101——0111

6——0110——001000

7——0111——001001

8——1000——001010

9——1001——001011

10——1010——001100

11——1011——001101

12——1100——001110

13——1101——001111

由此可见，如果数据出现小幅度的概率比出现大幅度的概率大，则通过指数哥伦布编码可以较好地压缩数据。但如果数据不满足上述特征，则压缩后的数据可能会比原来更大。

k阶指数哥伦布编码包含m位的0 + 1 位的1 + (m+k)位的数据，若要解码，对于某串k阶指数哥伦布编码的数据，先计算数据头部0 的个数，并记作m；则除去这m个0，该数据的有效位数为m+k+1，将该数据减去2k，即可得到指数哥伦布编码数据的解码，即原始数据。

由编码和解码的过程可知，解码能过完全恢复出编码之前的数据，不会损失数据的精度，因此指数哥伦布编码能够实现无损压缩。

单个数据的指数哥伦布编码很容易用硬件实现，然而要压缩的数据往往有很多个，在指数哥伦布编码之后通常要将这些数据拼接起来。由于这些数据往往不是整数字节，而且长度不一，这会导致数据的拼接需要消耗大量的逻辑资源。因此，指数哥伦布编码并不是熵编码的最佳选择。

2.4.2 整数字节熵编码

指数哥伦布编码之后的数据不是整数字节，而且长度也不确定，这给后续处理带来了很大的麻烦，下面考虑一种将差分编码后的数据压缩成整数个字节的熵编码。

对于24 bit 地震数据，一阶差分后的数据可用25 bit 表示，其大小位于[-16 777 216 , 16 777 215]区间，并且差分数据中的大多数数据数值都很小，因此可按照如下方式[5]压缩数据：

(1)如果差分数据位于[-64 , 63]区间，可用1 个字节A[7：0]表示该数据。A[6]为差分数据的符号位，A[7]=0，A[6：0]为差分数据的有效值。

(2)如果差分数据位于 [-8 192 , 8 191]区间，可用2 个字节B[15：0]表示该数据。B[13]为差分数据的符号位，B[15：14]=10，B[13：0]为差分数据的有效值。

(3)如果差分数据位于[-1 048 576 , 1 048 575]区间，可用3 个字节C[23：0]表示该数据。C[20]为差分数据的符号位，C[23：21]=110，C[20：0]为差分数据的有效值。

(4)无论如何，可用 4 个字节 D[31：0]表示该数据。D[24]为差分数据的符号位，D[31：25]=1 110 000，D[24：0]为差分数据的绝对值。

以上方法简单易实现，可将25bit 差分数据压缩为1～4 字节的数据。

由于压缩后的数据由若干个字节组成，因此如要解压，首先要判断哪几个字节（1 到4 字节）对应一个差分数据。首先从缓存区中读取一个字节的数据A[7：0]，如果A[6]=0，该数据为1 个字节；如果A[6：5]=10，该数据为 2 个字节；如果 A[6：4]=110，该数据为 3 个字节；如果 A[6：4]=111，该数据为 4 个字节。

先通过以上方法将差分后的数据分离出来，转换成25 bit 的数据；再进行差分逆变换，得到24 bit 的原始地震数据。

由编码和解码的过程可知，解码能过完全恢复出编码之前的数据，不会损失数据的精度，因此整数字节熵编码能够实现无损压缩。

如果地震数据不是24 bit，或者采用的差分编码不是一阶差分编码，也可以使用类似的整数字节熵编码。

3 FPGA 实现

为了减少传输节点需要上传的数据量，可以利用传输节点中的FPGA 对采集到的24 位地震数据进行压缩；当压缩后的数据到达船上时，再利用数据处理机箱中的FPGA 对数据解压。每个传输节点只负责压缩附近16 个传感器的地震数据。

因为对FPGA 的功耗有一定的要求，所以很难使用比较复杂的压缩算法。本文实现了一种用一阶差分编码和整数字节熵编码来完成地震数据压缩的算法。

3.1 数据压缩

使用一阶差分编码和整数字节熵编码来完成地震数据的压缩。在每一个采样周期内，需要输入24 bit 数据，然后输出1～4 字节的数据。数据压缩模块的输入输出端口如图4 所示。

数据的输入和输出均使用AXI-Stream 接口。输入的数据是24 bit 的地震数据，i_last 表示某一次压缩的最后一个数据；输出的数据是压缩后的数据，压缩后的数据以8 bit 为单位，o_last 表示压缩后数据的最后一个字节。数据压缩过程分差分编码和熵编码两步来实现。

3.1.1 差分编码

差分编码由一个24 位寄存器和一个24 位减法器实现，寄存器保存上一个数据，减法器利用当前输入的数据减去上一个数据得到差分数据，如图5 所示。图中：i_last 控制寄存器的清零（当最后一个数据到来时）；i_valid 和i_ready 控制寄存器的使能端（仅i_valid 和i_ready 都有效时才进行差分编码）。

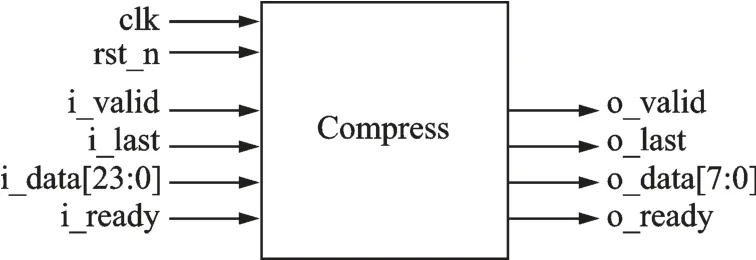
图4 数据压缩模块Fig.4 Module of data compression

图5 差分编码器Fig.5 Differential encoder

3.1.2 熵编码

整数字节熵编码可用一个组合逻辑电路来实现，输入25 位数据data_dif 和有效的字节数byte_cnt，输 出 4 字 节 数 据 data_out（1～4 字 节 有效），Verilog 代码如图 6 所示。

有效的字节数byte_cnt 可根据输入数据data_dif 高位多余的 0（负数为 1）得到。

在熵编码之后，需要将熵编码器输出的数据data_out[31：0]从 o_data[7：0]端口输出，根据 byte_cnt 的不同需要 1～4 个时钟周期。在输出完成之前，将i_ready 拉低，暂时停止前级的输入，直到输出结束才将i_ready 拉高。

图6 整数字节熵编码器的Verilog 实现Fig.6 Verilog implementation of integer byte entropy encoder

3.2 数据解压

数据解压在船上数据处理机箱中的FPGA 上进行。数据解压模块也是使用AXI-Stream 接口，输入8 bit 压缩数据，输出24 bit 地震数据。数据解压过程分反熵编码和反差分编码两步。

3.2.1 反熵编码

反熵编码的第1 步是根据每个压缩数据的第一个字节来判断该数据占用了几个字节，然后将这几个字节的数据当作反熵编码器的输入，并开始解析下一个数据，该过程可以通过一个状态机来实现。

反熵编码器则可以通过一个简单的组合逻辑电路实现，输入4 字节数据data_in（1～4 字节有效）和有效的字节数byte_cnt，输出25 bit 数据data_dif，Verilog 代码如图 7 所示。

有效的字节数byte_cnt 通过反熵编码第一步的状态机得到。

3.2.2 反差分编码

类似于差分编码，反差分编码可用一个25 位寄存器和一个25 位加法器实现，寄存器保存之前所有数据的和值（即上一个原始数据），加法器将当前差分数据和上一个原始数据相加得到当前原始数据，如图8 所示。图中：i_last 控制寄存器的清零（当最后一个数据到来时）；i_valid 控制寄存器的使能端（仅i_valid 有效时才进行反差分编码）。

图7 反熵编码器的Verilog 实现Fig.7 Verilog implementation of inverse entropy encoder

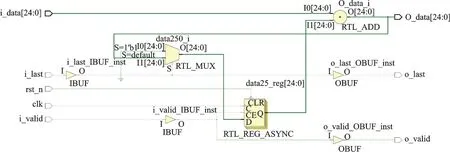
图8 反差分编码器Fig.8 Inverse differential encoder

4 测试结果

4.1 压缩率

压缩率指数据压缩之后的大小与数据压缩之前的大小之比。利用本文中所述的一阶差分编码和整数字节熵编码，表1 给出了3 组实测地震数据的压缩结果。

每一组地震数据均由2 336 个传感器进行12 288 次采样得到。每次压缩1 个传感器64 次采样得到的地震数据，压缩前数据长度为64×3=192 字节。总压缩次数为2 336×12 288/64=448 512 次。剔除掉全零数据（采集系统未开始工作），需要压缩的次数记作总帧数。使用本文中所述的压缩算法压缩这些数据，记录这些数据在压缩之后的总长度（记作总字节数）。压缩后的平均长度=总字节数/总帧数。压缩率=平均长度/192。3 组地震数据的平均压缩率=（101+105+105）/3/192=54%。

4.2 资源占用

数据压缩在传输节点中的FPGA 上进行，相应FPGA 的型号是Altera 公司的Cyclone V 5CEBA7F23C7，压缩模块占用的资源如图9 所示。压缩模块需要的逻辑资源为54 个ALMs，不到总量的千分之一。

数据解压在船上数据处理机箱中的FPGA 上进行，FPGA 的型号为Xilinx 公司的Kintex-7 xc7k325tffg900-2，解压模块占用的资源如表2 所示。解压模块需要的逻辑资源为79 个LUT，不到总量的万分之五。

由此可见，不管是压缩模块，还是解压模块，占用FPGA 的资源都可以忽略不计。

表1 压缩率测试结果Table 1 Test result of compression ratio

图9 压缩模块占用资源Fig.9 Utilization of compression module

表2 解压模块占用资源Table 2 Utilization of decompression module

4.3 仿真结果

图10 是压缩模块的仿真结果。在图10 中，采集的24 位数据依次是{580，600，630，900，-900（}3 字节带符号整数），压缩后的数据依次是{82，44，14，1E，81，0E，E0，FF，F8，F8（}十六进制）。可以发现，相邻两个数据之间的差值越小，则数据压缩之后的长度也会越小。同时，由于压缩一个数据需要多个时钟周期（1～4 个），因此输入的数据之间应该间隔若干个时钟周期。

图11 是解压模块的仿真结果，直接利用压缩模块的仿真结果当作解压模块的输入，输入数据依此为{82，44，14，1E，81，0E，E0，FF，F8，F8（}十六进制），输出的数据是{580，600，630，900，-900（}3 字节带符号整数）。可以看出，解压得到的数据正是压缩之前的数据。

图10 压缩模块仿真结果Fig.10 Simulation result of compression module

图11 解压模块仿真结果Fig.11 Simulation result of decompression module

5 结束语

海洋地震勘探方法是目前海洋油气勘探的主要方法，更深层和更精确的海洋勘探需要更长的勘探拖缆，这将导致系统的功耗和传输速率大幅度增加。本文提出了一种可以提高传输效率的24位地震数据流无损压缩算法，可以大幅度降低采集系统需要的传输速率，同时略微降低采集系统的功耗。地震数据的压缩率平均可达54%，数据压缩算法很容易用FPGA 实现，占用FPGA 的逻辑资源极少，无须占用或只需占用较少的存储资源，数据压缩可在几个时钟周期之内完成。简而言之，本文所述的压缩算法可以只花费极少的代价就将地震数据采集系统需要传输的地震数据量减少一半左右。