基于超声迟到回波的固体弹性模量测量

杨海楠

（1.中国商用飞机有限责任公司北京民用飞机技术研究中心，北京，102211；2.民用飞机结构与复合材料北京市重点实验室，北京，102211）

引 言

弹性性能是材料力学性能中一项重要的指标，反映材料在弹性变形阶段的工作特性[1-2]。纵向应力与纵向应变的比例常数就是材料的弹性模量，是材料刚性的标志[3]。由于航空工业的特殊性，一些零部件为外部供应商提供，出于保密的原因无法获取具体材料参数，需要对其弹性模量进行测量，这对于结构状态监测结果的校准是至关重要的。

超声法是通过测量固体材料中两个模式的超声波声速，例如纵波和横波，推算出材料的弹性模量[4-5]。其原理是固体材料中超声波的声速与材料弹性模量、泊松比和密度具有固定关系，所以对已知密度材料的声速进行测量就可以计算出弹性模量[6-8]。利用超声法可以实现对弹性模量的无损、快速和高精度测量，适用范围广泛[9-11]。

目前国内外在固体材料声速测量方面采用的方法大多为单探头反射法或双探头穿透法［12-14］。对于纵波声速，可以通过测量超声波通过一定距离所需的时间来得到［15-16］。相较而言，横波声速的测量较为复杂。目前普遍应用的方法有两种，一种是利用纵波斜探头在圆弧形试块中产生纯横波，通过声程（圆弧形试块半径）和回波时间计算横波声速；另一种是利用横波直探头测量横波声速。圆弧形试块法需要额外制造试块，时间成本和材料成本高，当材料特性未知时就更加难以实现；横波直探头法需要使用价格较高的横波探头。以上问题导致这两种方法的应用受到局限。

本文提出了一种基于超声脉冲回波检测中迟到回波的横波声速测量法，该方法不需要额外制造试块和横波探头，也不需要复杂的设备，只需利用最常用的超声检测仪和纵波直探头对材料横波声速进行测量，进而计算得出材料弹性模量，并通过实验验证了该方法的有效性。

1 基于超声的弹性模量计算原理

对于一种各向同性的固体介质，其纵波声速CL和横波声速CS是由介质的密度、弹性模量和泊松比决定的，且有如下关系

式中：Ε为弹性模量，μ为泊松比，ρ为介质密度。

根据式（1，2），弹性模量为

式中T=CL/CS。通过准确测量介质的纵波和横波声速，即可计算得到介质的弹性模量。下面重点说明纵波声速与横波声速的测量原理。

1.1 纵波声速的测量原理

为了得到介质的纵波声速，可以利用超声波扫描设备，将超声探头垂直入射试件，得到反射波的波达时间，计算纵波声速

式中：d为试件厚度，Δt为入射波与反射波之间的时间差。

对于只能显示反射波声程，而不能直接显示超声波传播时间的超声检测仪器，可通过调节仪器上的波速设置项，使得表面波和底波两闸门之间的显示声程恰好等于试验件厚度，则此时设置的波速即为纵波声速。

1.2 基于迟到回波的横波声速测量原理

迟到回波是在1 次底波后出现在固定位置的特殊回波[17]，它是由于超声波在介质中传播时因经过不同的路径或发生波形转换，从而延迟到达探头。这种特殊回波在利用纵波直探头从细长或扁长试件的纵向检测时会出现，其测量及超声波形示意图如图1 所示。

图1 横波声速测量及超声波形示意图Fig.1 Schematic diagram of transverse wave velocity measurement and ultrasonic waveform

当探头发出的纵波IL沿试件上表面传播时，根据斯奈尔定律，会同时由于波形转换产生一个沿α角度传播的横波RS1，并且

当横波RS1传播到试件下表面时，又会由于波形转换产生一个反射横波RS2和沿下表面传播的反射纵波RL1，反射横波RS2到达上表面后，又会由于波形转换产生一个沿上表面传播的反射纵波RL2，以此类推。则IL、RL1和RL2等一系列沿试件上下表面传播的纵波被试件底面反射后由探头接收，则在1 次底面波之后产生一系列迟到回波，且各个迟到回波之间的延迟时间Δτ为横波通过声程AB所需的时间减去纵波通过声程CB的时间，即

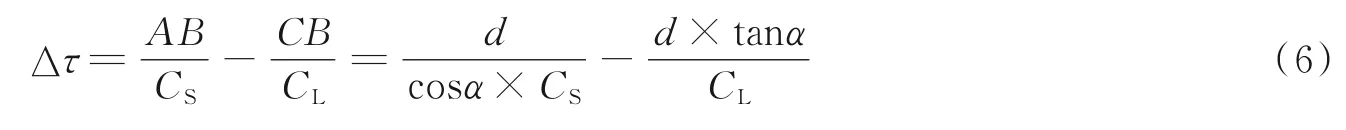
则换算可得横波声速计算公式为

将结果代入式（3）即可求得试件的弹性模量E。

对于只能显示反射波声程，而不能直接显示超声波传播时间的超声检测仪器，则不能直接从仪器上读取迟到回波的延迟时间Δτ，而只能读出延迟声程Δs，由于此类设备的声程显示结果为设定波速与时间差乘积的一半，则Δs的显示结果为延迟时间Δτ与纵波声速CL乘积的一半，即

所以，通过直接在仪器上读出延迟声程Δs，就可以利用式（8）计算出角度α，再利用式（5）计算出横波声速CS，最后代入式（3）即可求得试件的弹性模量E。

该方法也存在一些局限性，即要求至少能够在仪器上清晰显示两个迟到回波，即

由此可见，超声检测仪显示出的迟到回波的个数取决于试件的长度和厚度的比值。

2 实验验证

为了验证上述理论的有效性，本文利用实验的方法对一个材料为4340 牌号的长方体合金钢试件进行了弹性模量的测量。该合金钢的材料参数如表1 所示。

表1 4340 牌号合金钢材料参数［18］Table 1 Material parameters of 4340 alloy steel［18］

实验用到的仪器设备及工具包括超声检测仪、超声探头、游标卡尺和电子秤等，其设备信息如表2所示。

表2 实验设备信息Table 2 Experimental equipment information

2.1 密度测量

为计算弹性模量，需要测量试件的密度。其方法为利用游标卡尺测量试件的三维尺寸，计算出试件体积V，对于形状不规则试件，也可用排水法测量试件体积，再利用电子秤测量试件质量m,则密度为

实验测得试件三维尺寸为119.66 mm×15.20 mm×15.14 mm = 27 537.12 mm3，质量为215.0 g，所以经过计算，试件密度为7 807.64 kg/m3。

2.2 纵波声速测量

采用1.1 节的方法测量试件中的纵波声速。利用游标卡尺测量试件长度为119.66 mm，将超声探头置于已涂覆耦合剂的试件端面上，将超声检测仪上的闸门分别设置于超声波形的1 次底波和2 次底波上，调整超声检测仪上波速的设置值，使得声程显示值等于游标卡尺测得的试件长度，此时波速设置值即为该试件的纵波声速值CL。超声波形如图2 所示，测量得到的纵波声速为5 925 m/s。

2.3 横波声速测量

采用1.2 节的方法测量试件中的横波声速。将超声探头置于已涂覆耦合剂的试件上纵向端面上，将超声检测仪上的闸门分别设置于1 次底波后出现的2 个迟到回波上，读取此时的声程值Δs，利用游标卡尺测量试件厚度d为15.14 mm，然后利用式（8）计算出角度α，最后利用式（5）和测得的纵波声速，计算出横波声速CS。为了提高测量精度，分别测量第1 次和第2 次迟到回波之间的Δs1为11.45 mm，第 2 次 和 第 3 次 迟 到 回 波 之 间 的 Δs2为11.49 mm，超声波形如图3 所示。计算出的横波声速取平均值为3 263.76 m/s，结果如表3 所示。

此外，利用游标卡尺测量试件长度L=119.66 mm，代入式（9），得到迟到回波个数为10 个，与波形图中的迟到回波个数相同，证明了该测量原理的正确性。

2.4 弹性模量计算

至此，已通过实验的方法得到了计算弹性模量所需要的所有数据，将2.1 节得到的试件密度7 807.64 kg/m3、2.2节得到的纵波声速5 925 m/s 和2.3 节得到的横波声速3 263.76 m/s 分别代入式（3）得

图2 纵波声速测量波形图Fig.2 Longitudinal wave velocity measurement chart

图3 横波声速测量波形图Fig.3 Transverse wave velocity measurement chart

表3 横波声速测量值Table 3 Transverse wave velocity measurement result

得到弹性模量计算值为213.28 GPa。所得结果与理论值对比的相对误差如表4 所示。

由此可见，利用常规法测量得到的试件密度、通过超声法测量得到的纵波和横波声速与理论值相比，相对误差很小，说明各自使用的方法是准确有效的。利用上述测量结果通过计算得到的试件弹性模量与理论值相比同样误差很小，说明该弹性模量的计算方法也是正确的。

表4 测量结果与理论值相对误差Table 4 Relative error between measurement result and theoretical value

2.5 测量不确定度及误差分析

为评估弹性模量测量的不确定度，采用2.1—2.3 节的方法，对试件的弹性模量共进行了5 次测量，并计算了测量结果的平均值和标准偏差，结果如表5 所示。

表5 弹性模量多次测量结果平均值与标准偏差Table 5 Average and standard deviation of elastic modulus of multiple measurement results

测量不确定度表示被测量的分散性，可通过测量标准偏差来表征，本次实验验证共进行了5 次测量，标准偏差为0.61 GPa，表明测量不确定度较小，测量分散性较低，可信赖程度较高。同时，测量值与理论值相比误差较小，对存在误差的可能原因进行了分析，包括实验中用到的测量器具存在的误差，实验人员操作过程导致的误差和随机噪声造成的误差等。其中造成误差的随机噪声主要分为两类，一类是超声波峰之间波幅极低的噪声信号，另一类是叠加到波峰之上而影响波幅的噪声信号。为了降低随机噪声导致的误差，在设置闸门时，应将闸门位置远离波峰底部和顶部，以保证波形上升沿取值的准确性，等待显示值稳定后再读取数据，降低由随机噪声导致的测量误差。

3 结束语

弹性模量是反映固体材料力学性能的重要参数，本文以未知材料特性固体结构弹性模量的测量为需求，以超声检测原理为背景，以固体材料物理参数与力学特性之间的固有关系和超声检测中的迟到回波现象为原理，提供了一种利用超声检测仪和普通纵波直探头，通过分别测量试件纵波和横波声速，进而计算试件弹性模量的方法。通过实验验证，本文研究结论如下：

（1）通过对已知材料特性的4340 牌号钢材试件分别进行密度、纵波声速和横波声速的测量，结果与理论值对比误差很小，证明测量原理和实验过程准确有效。

（2）根据测量结果计算弹性模量，与试件理论材料参数进行对比，相对误差很小，证明弹性模量计算方法正确。

（3）实验结果表明，可以利用该方法对材料特性未知的试件进行快速、准确和低成本的弹性模量测量，是一种测量未知材料特性试件力学性能的通用方法，具有较为广泛的应用前景。