基于改进头脑风暴优化算法的医学图像配准方法

曹国刚，朱信玉，陈 颖，曹 聪，孔德卿

（上海应用技术大学计算机科学与信息工程学院，上海，201418）

引 言

由于单一模态的医学图像难以提供充足的病灶信息，通常将多模态的医学图像进行融合，从而辅助医生诊断。在进行图像融合前，需要对患者的医学图像进行配准，即在参考图像与浮动图像之间通过寻优算法找到最优的空间变换参数，使两幅图像在误差最小的情况下对齐，其本质是参数优化问题[1-3]。

经典医学图像配准框架主要包括测度函数、优化算法、空间变换、插值4 个方面。其中，相似性测度是图像配准结果的衡量指标，测度函数值用来表示两幅图像的对齐程度[4]。常见的测度函数包括互信息(Mutual informational, MI)、条件方差和(Sum of conditional variance, SCV)[5]、归一化互信息(Normalized MI, NMI)[6]、交叉累计剩余熵(Cross cumulative residual entropy, CCRE)[7-8]、归一化互相关(Normalization cross-correlation, NCC)[9]等。寻优算法在图像配准的过程中对配准精度与速度起到决定性作用。当前优化算法主要分为局部优化算法与全局优化算法两种，常用的局部优化算法包括梯度下降法、Powell 算法、单纯形搜索法，全局优化算法包括遗传算法、差分进化算法[10-11]、粒子群算法[12-13]等。测度函数普遍存在多极值问题，因而仅使用局部搜索算法难以逃离局部最优，虽然全局搜索算法可以跳出局部最优，但此类算法存在计算量大、收敛速度慢等问题。在医学图像配准领域，采用多分辨率策略可以充分结合局部优化算法和全局优化算法的优点，有效地缩短运算时间，同时保证较高的配准精度。如文献[14]将粒子群优化算法（Particle swarm optimization, PSO）与单纯形搜索法（Simplex）相结合使用多分辨率策略对医学图像配准，其精度优于Powell、Simplex、PSO 三种算法。文献[15]将自适应差分算法与Powell 相结合应用于医学图像配准，配准精度达到了亚像素级。文献[16]将头脑风暴优化算法与Powell 相结合，与遗传算法、粒子群算法、蚁群算法与Powell 结合算法进行比较，配准结果均方根误差与配准时间均得到了一定程度的降低。

为了进一步提高配准算法的精度与收敛速度，本文基于多分辨率策略开展了以下3 方面的工作：（1）改进了头脑风暴优化算法，提出一种改进头脑风暴优化（Improved brain storm optimization ，IBSO）算法；（2）提出一种基于多分辨率策略的医学图像配准算法，该算法在低分辨率层使用IBSO 粗配准，高分辨使用单纯形搜索法精配准；（3）对提出的配准算法分别完成了MRI-MRI单模态与CT-MRI多模态实验。

1 医学图像配准方法

1.1 相似性测度

MI 源自于信息论，用于表示浮动图像F包含参考图像R的信息量。因互信息作为测度函数无需特征提取且配准精度高，因而本文在单模态配准实验中采用其作为测度函数评价配准效果。R与F的互信息定义为

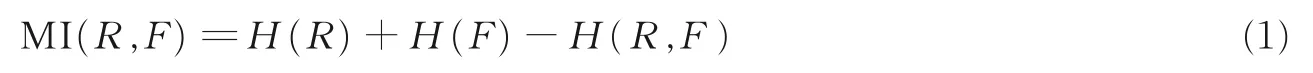
式中：H(R)、H(F)分别表示参考图像R、浮动图像F包含的信息量，如式（2）和（3）所示；H(R,F)为R和F的联合熵，其定义如式（4）所示。

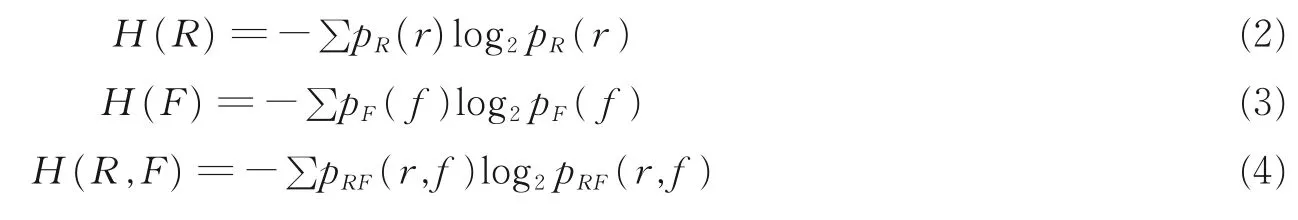
多模态图像配准时，采用互信息作为测度函数容易受到参考图像R与浮动图像F重叠程度的影响，导致测度函数曲线不光滑。Studholme 等[6]提出NMI 可以解决上述问题，因而在多模图像配准中使用广泛，其定义为

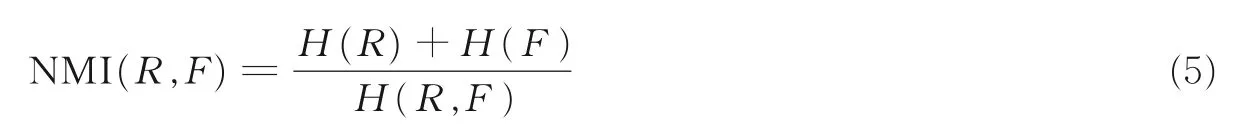
NCC 是另一种常用的测度函数，其取值范围为[0,1]，NCC 系数越趋近于1 代表配准精度越高，其定义为

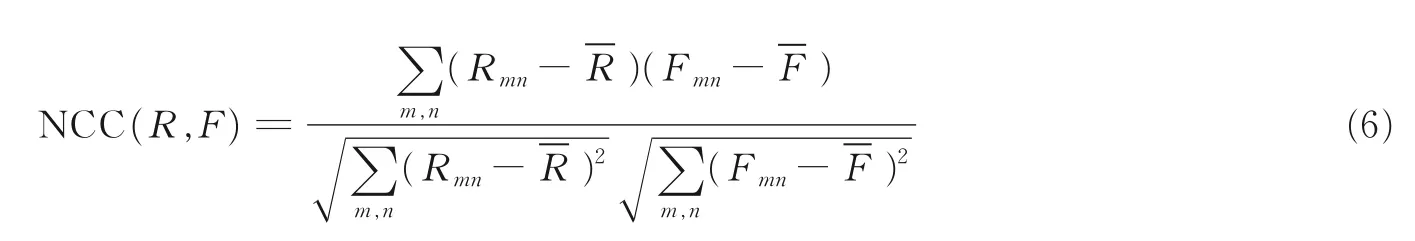
Wang 等[8]基于累计剩余熵理论提出一种CCRE 测度,其通过实验证明了CCRE 具有较高的鲁棒性，CCRE 定义为

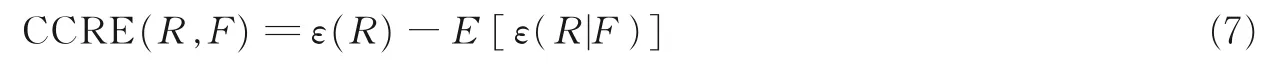
式中：ε(R)为累计剩余熵函数，表达式为

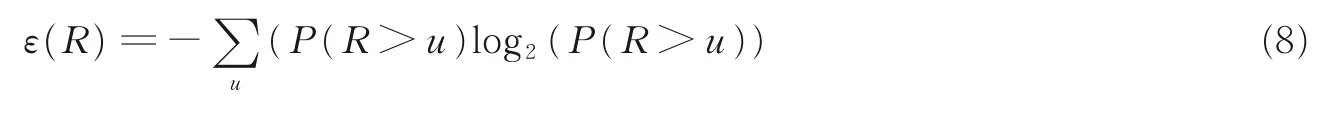
式中：P(R＞u)代表图像R的像素点比灰度值u高的概率。

1.2 多分辨率策略

局部搜索算法容易陷入局部最优，而全局优化算法运算时间长。为了平衡配准的效率与精度，在医学图像配准领域常常对待配准图像进行两层小波分解[17]，由原图像及小波分解后的图像构成图像金字塔，其模型如图1 所示。

小波变换将时域信号变换成频域信号，小波分解后图像的低频成分保留原始图像的基本信息，高分辨率图像保留图像的细节部分以及夹杂了高频噪声。因此在低分辨率的图像上使用全局寻优算法进行粗配准，得到寻优参数作为局部寻优算法的初始点，再对高分辨率图像进行精配准是医学图像配准领域一种常用的配准策略。

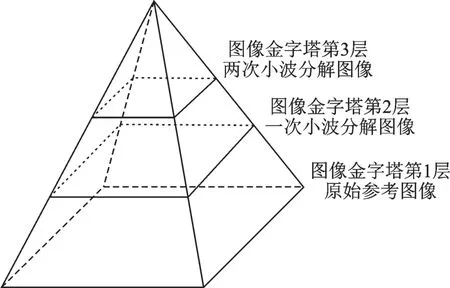
图1 图像金字塔模型Fig.1 Model of image pyramid

1.3 头脑风暴优化算法

基于人类头脑风暴过程建模，Shi 于2011 年提出了头脑风暴优化算法(Brain storm optimization algorithm, BSO)[18]，并于2016 年又进行了综述[19]。BSO 算法将种群中每个想法个体看作是d维问题的一个潜在解，种群中第i个想法个体可表示为

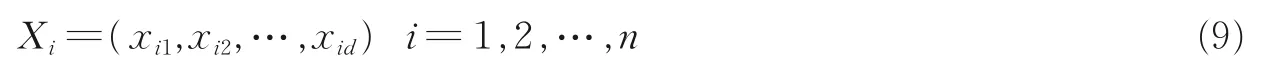
头脑风暴优化算法首先根据问题的规模产生想法种群并初始化，然后在每次迭代中对想法种群进行聚类、变异、产生新个体和选择操作。

（1）聚类。将想法种群聚成m个子群，在每个子群中根据个体的适应度值进行排序，选择最优适应度值的个体作为每个子群的聚类中心。

（2）变异。生成随机数p1，其取值范围为[0,1]，如果p1小于预设概率ppre1则生成一个新个体取代随机选择的聚类中心。

（3）产生新个体。生成随机数p2，其取值范围为[0,1]，将其与预设概率ppre2进行比较：

① 如果p2≤ppre2，随机选择一个子群同时生成[0,1]之间随机数p3，与预设概率ppre3比较，（a）如果p3≤ppre3，选择聚类中心作为线索用于产生新个体；（b）如果p3＞ppre3，随机选择该子群中的一个想法个体作为线索用于产生新个体。

② 如果p2＞ppre2，随机选择两个子群同时生成[0,1]之间随机数p4，与预设概率ppre4比较，（a）如果p4≤ppre4，选择两聚类中心作为线索用于产生新个体；（b）如果p4＞ppre4，随机在两个子群中选择两个个体作为线索用于产生新个体。

（4）选择。将产生的新个体与被选择个体进行适应度值比较，选择其中适应度值高的个体进入新一轮迭代。

（5）若达到最大迭代次数或满足最优解条件则停止迭代，输出结果，否则转步骤1，开始新一轮迭代。

为了保证新产生的想法尽可能地利用现有的想法，通常采用在线索个体中添加噪声的方式来产生新想法个体。通过已存在的想法xold产生一个新想法xnew，可以表示为

式中：T为最大迭代次数；t为当前迭代数；k用于改变 logsig(∙)函数斜率，文献[14]证明参数k为 25 是个不错的选择。

1.4 单纯形搜索法

单纯形搜索法是一种高效的局部搜索算法，常用于求解无约束最优化问题。单纯形指的是n维空间Rn中具有n+1 个顶点的凸多面体。单纯形搜索法的基本步骤如下：给定Rn中的一个单纯形后，分别求出n+1 个顶点处的函数值，确定出其中函数最大值点及函数最小值点，然后通过反射、扩展、压缩等几种方式求出一个较好的点来替代目前函数最大值点组成新的单纯形，或者向函数最小点方向收缩构成新的单纯形。通过多次的迭代，逐渐收缩单纯形范围，逼近函数最小值点。

单纯形搜索法在局部搜索时具有搜索效率高、速度快等优势。但初始点对其十分重要，当初始点距离局部最优点较近时，算法难以逃离局部最优。为了避免单纯形搜索法的这一缺陷，本文算法将单纯形搜索法初始点设置为全局寻优算法求得的全局最优的粗略位置。

2 IBSO 算法及其在医学图像配准中的应用

2.1 IBSO 算法

BSO 在每一次迭代中通过聚类、变异操作使种群个体向最优解收敛。在聚类过程中，每个子群中适应度值最优的个体被选择作为聚类中心，其在算法的迭代过程中具有优势地位。BSO 通过向线索个体添加噪声的方式生成新个体，而聚类中心相对普通个体具有较高的概率被选择作为线索个体。

观察算法的迭代过程可以发现：迭代后期阶段每个子群的聚类中心基本稳定，最优的聚类中心个体是当前迭代的最优解，而最差聚类中心在搜索的后期阶段基本处于停滞更新状态。

为了保证所有个体均参与当前的优化搜索过程，加快收敛速度，本文提出IBSO 算法。IBSO 在每次迭代聚类过程结束后，对当前最差的聚类中心进行改进。选择当前最优聚类中心Cen(best)作为线索个体，根据式（10）生成新个体，计算新生成个体的适应度值，与当前最差聚类中心个体的适应度值进行比较，选择适应度值高的个体进入下一次迭代过程，选择条件如式（14）所示，IBSO 算法流程如图2 所示。

式中：Cen(worst)为适应度值最差的聚类中心；Cen(gen)为将当前最优聚类中心作为线索生成的新个体；Fit()为适应度函数，Fit(Cen(worst))为原最差聚类中心适应度值，Fit(Cen(gen))为新产生个体的适应度值。

使用最优聚类中心作为线索生成的新个体是极具潜力的个体，将其替换最差聚类中心个体，一方面，可以使种群所有个体在算法的后期搜索阶段均处于活跃状态。另一方面，IBSO 算法每次迭代均把最差聚类中心替换掉，可以加快种群个体向最优解的逼近速度。

图2 IBSO 算法流程图Fig.2 Flowchart of IBSO algorithm

2.2 IBSO 算法在医学图像配准中的应用

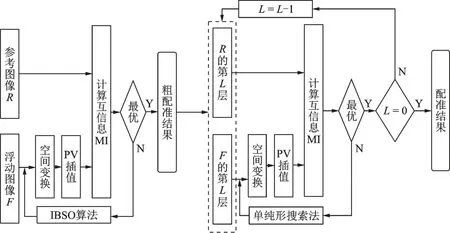
本文将IBSO 算法的全局搜索能力与单纯形搜索法的局部搜索能力进行优势互补，使用两种算法协作完成医学图像配准任务。首先，将原始图像进行小波分解，分解后的图像构成图像金字塔；然后，在低分辨率层使用IBSO 算法进行全局寻优；最后，将IBSO 算法的寻优值进行倍率缩放后作为单纯形搜索法的搜索起点，在金字塔的第2 层及第1 层使用单纯形搜索法进行局部搜索。具体算法步骤如下：

步骤1将待配准图像R和F进行两次小波分解，源图像作为图像金字塔的第1 层图像，第一次小波分解图像作为金字塔第2 层，对第一次小波分解的图像进行第二次小波分解作为图像金字塔的第3层。若高一层的寻优参数为(x,y,θ)，则(2x,2y,θ)作为下一层初始参数，平移参数翻倍，旋转参数值保持不变。

步骤2使用IBSO 算法作为寻优函数对图像金字塔顶层图像配准，在单模图像配准时使用MI 作为配准的测度函数，多模配准将MI、NMI、NCC、CCRE 分别作为配准的测度函数进行实验。

步骤3将IBSO 寻优算法得到的参数做相应的倍率缩放后作为单纯形搜索的搜索起点，搜索图像金字塔的第2 层图像。

步骤4将步骤3 中寻优结果进行相应的倍率缩放后，在图像金字塔第1 层即原始图像上进行寻优。寻优结束，得到配准参数(x,y,θ)，使用上述配准参数对浮动图像F进行空间变换，融合变换后的浮动图像与参考图像（图3）。

3 实验与结果分析

为了验证本文所提算法的稳定性与有效性，分别对MRI-MRI 单模态与CT-MRI 多模态医学图像进行配准。实验环境为：Windows10 操作系统，Matlab R2018a 实验平台。硬件平台为：Intel(R)Core(TM)i7-9750H CPU@2.60 GHz、内存16 GB。本文方法与3 种主流配准算法比较算法误差、耗时、配准精度等参数，3 种算法分别为 PSO 与 Simplex 的结合[14]、差分进化（DE）算法与 Powell 算法的结合[15]、BSO 算法与 Powell 算法的结合[16]。以上 3 种算法分别记为 PSO+Simplex、DE+Powell、BSO+Powell。PSO、DE、BSO 与 IBSO 种群规模均为 50，PSO、DE、BSO、IBSO、Simplex、Powell 算法最大迭代次数均为200，其他参数与文献[14-16]保持一致。

3.1 单模态配准实验与结果分析

单模态医学图像配准采用BrainWeb 医学图像数据集。参考图像R选取MRI-T1 加权图像的第90层切片，切片厚度为1 mm，噪声水平0%，如图4(a)所示。浮动图像F是在参考图像的x轴方向平移7 像素、y轴方向平移3 像素，绕中心旋转5°得到。对每种优化算法重复进行100 次实验，统计其平均误差、最大误差和平均耗时。

图4 单模态配准融合图像Fig.4 Mono-modality registration fusion images

单模态配准结果如表1 所示，其中Δx、Δy分别表示x、y方向的平移量误差，Δθ表示旋转的角度误差。maxΔX、maxΔY分别表示 100 次实验中x、y方向的最大平移量误差，maxΔθ表示 100 次实验中旋转的角度最大误差。当平移量误差小于1 像素，旋转角误差小于1°称本次配准达到了亚像素级[13]。

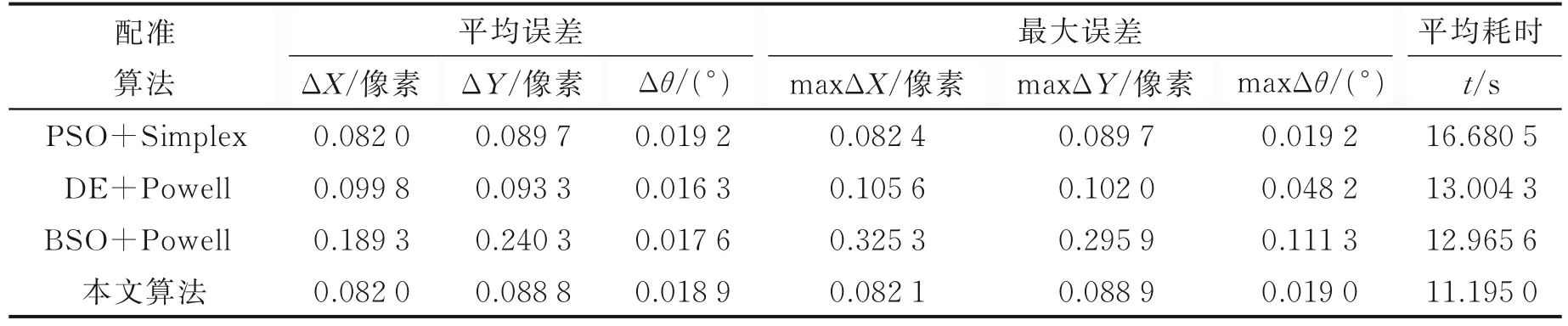
表1 单模态图像配准实验结果对比Table 1 Comparison of experimental results of mono-modality image registration

观察表1 可以发现4 种配准算法均可以达到亚像素级配准。综合来看，与PSO+Simplex 和BSO+Powell 算法相比，本文算法的平均误差、最大误差均得到了一定程度的降低，平均耗时较两种配准算法分别降低了32.89%和13.66%；与DE+Powell 算法相比，本文算法角度误差略高，其余指标均得到一定程度的优化，且平均耗时降低了13.91%。

3.2 多模态配准实验与结果分析

多模态图像配准采用Vanderbilt 大学Retrospective Image Registration Evaluation Project,Version 2.0 数据集。配准结果采用MI、NCC、NMI、CCRE 4 种相似性测度函数作为指标对配准结果进行评价，相似性指数的值越高代表参考图像与浮动图像配准效果越好。表2 为4 种配准算法对参考图像与浮动图像分别使用MI、NMI、NCC、CCRE 作为测度函数进行100 次配准实验结果的平均值。配准结果显示本文算法MI、NMI、CCRE 与 NCC 均 优 于 其 他 3 种 配 准 算 法 。图 5（a）为 CT 参考图像，图 5（b）为 MRI-T1 浮动图像，图 5（c）—（f）分别为 PSO+Simplex、DE+Powell、BSO+Powell 和本文算法对参考图像与浮动图像配准融合后的图像。

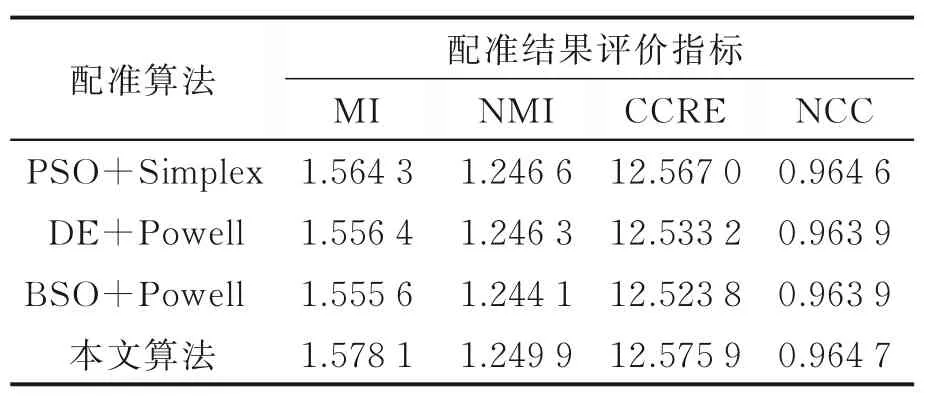
表2 多模态配准实验结果对比Table 2 Comparison of experimental results of multimodality registration

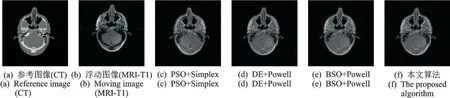
图5 多模态配准融合图像Fig.5 Multi-modality registration fusion images

单模态与多模态配准结果表明，本文算法较PSO+Simplex、DE+Powell、BSO+Powell 配准算法在速度方面得到了一定幅度的提升，这得益于在IBSO 中每次迭代过程均使用当前最优解作为线索生成新个体替代本次迭代最差聚类中心，使算法收敛速度大大提高。虽然，在每次迭代中替换最差聚类中心个体的操作可以使得算法收敛速度显著提高，但这个操作同时降低了原始BSO 的种群多样性，增大了算法早熟收敛的风险。从配准结果来看，本文算法各项指标均有不同幅度的提升，较上述3 种配准算法性能优越，具有更高的临床使用价值。

4 结束语

为了克服测度函数局部极值多、配准消耗时间长等问题，本文采用多分辨率策略，将改进头脑风暴优化算法与单纯形搜索法相结合提出一种新的配准方法，并将该方法与3 种主流配准算法进行了单模态与多模态配准的实验对比。实验结果表明，本文算法在有效提高医学图像配准精度的同时缩短配准所用的时间，具有更高的临床使用价值。所提算法目前在颅脑MRI-MRI、颅脑CT-MRI 图像配准实验中取得了较好的配准效果。而临床诊断与治疗中CT-PET、US-MRI 等多模态图像之间的配准同样具有很高的实用价值，这些多模态配准图像因其成像差异需要选定不同的测度函数评估其对齐程度。本文重点研究了配准过程中的优化算法，将其与更多相似测度结合应用于其他多模态图像配准是下阶段的主要工作。