邻域互补信息度量及其启发式属性约简

2020-08-11张贤勇唐玲玉姚岳松

数据采集与处理 2020年4期

陈帅，张贤勇，唐玲玉，姚岳松

（1.四川师范大学数学科学学院，成都，610066；2.四川师范大学智能信息与量子信息研究所，成都，610066）

引言

信息理论能够有效实施不确定表示与应用[1]，已经被系统地引入粗糙集进行数据分析与智能处理。例如，文献[2-5]采用香农熵、粗糙熵和加权熵等体系进行不确定性刻画与约简算法启发。特别地，文献[6]基于互补机制提出互补信息体系，相关不确定性度量包括互补熵、互补条件熵和互补互信息，它们刻画了粗糙性与模糊性。继而，文献[7]以互补条件熵为启发式信息，构建基于正域的属性约简算法；文献[8]基于三层粒度结构，构建三支加权互补熵体系。互补信息度量采用的互补刻画p(1-p)区别于香农信息度量的对数刻画-plog2p，但两者具有一些共同特征(如函数上凸非单调)，进而也存在一定相似性(如度量系统关系)。对比于香农信息体系，互补信息系统能够有效刻画粗糙集的模糊性[6]。可见，互补信息度量具有独特的不确定性刻画优势，但其研究还相对较少，相关的深入与拓展具有创新价值。

粗糙集具有双向逼近认知，能够进行知识约简与特征选择，广泛应用于数据挖掘、机器学习和人工智能等领域。传统粗糙集主要采用等价关系与知识剖分，相关数值型数据处理往往需要离散化。邻域粗糙集引入邻域关系与覆盖结构，具有理论扩张性与应用鲁棒性，能够有效处理符号型数据、数值型数据乃至混合型数据。邻域粗糙集的不确定性度量与属性约简得到了广泛研究[9-15]。特别地，文献[16]建立基于对数函数-log2p的信息体系(包括邻域熵、邻域条件熵和邻域互信息)；文献[17]用邻域互信息进行特征选择与多标签学习；文献[18]提出邻域精度、邻域熵、信息粒度及相关粒化单调性；文献[19]建立一种模糊熵来度量邻域粗糙集的不确定性；文献[20]采用邻域熵及其发展度量进行离群点检测。总之，邻域粗糙集尚未涉及互补信息度量体系，相关的构建具有应用意义。

基于上述背景，本文拟将经典互补信息度量推广到邻域粗糙集，并研究相关的启发式属性约简。基于邻域扩张，具体构建邻域互补熵、邻域互补条件熵和邻域互补互信息，研究基本性质；基于邻域互补互信息及其粒化非单调性，设计属性约简及其启发算法。研究结果被决策表实例与UCI 数据实验有效验证，并有利于基于邻域粗糙集的不确定性信息处理。

1 经典邻域互补信息度量与邻域系统

本节利用文献[6,8]与文献[16,21]分别回顾经典互补信息度量与邻域系统。

决策表为四元组DT=(U,AT=C∪D,V,f)，U为有限论域，C,D分别为条件、决策属性集,V=∪a∈AT Va(Va是属性a∈AT的值域)，信息函数f：U×AT→V具有 ∀x∈U，∀a∈AT，f(x,a)∈Va。设条件属性子集A⊆C诱导知识划分决策属性集D诱导决策分类 }；设∗C=U-∗表示补集，例如。

定义1[6,8]A⊆C的互补熵、D相对于A的互补条件熵、A与D之间的互补互信息分别为

定理1[6,8]互补熵、互补条件熵、互补互信息满足如下系统方程

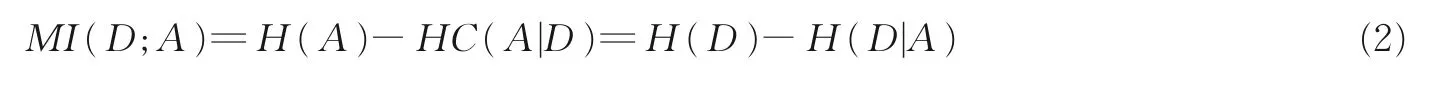
式中

定理 2[6,8]若U/IND(A)≥U/IND(B)( 即 ∀ [x]B∈U/IND(B)，∃[x]A∈U/IND(A)，s.t.[x]B⊆ [x]A)，则

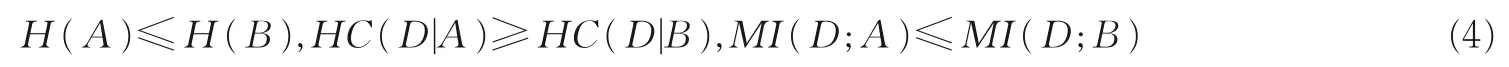
定义1 提供了经典互补信息体系，其涉及补集描述与概率形式(如即其采用对称二次函数p(1-p)替换经典的非对称对数函数-plog2p进行信息集成，从而成为一种新型不确定性度量，互补熵刻画条件知识结构的不确定性，互补条件熵与互补互信息描述条件结构与决策结构之间的信息关系，相关体系可以度量粗糙性与模糊性等不确定性[6]。事实上，U/IND(A)与U/IND(D)具有关于等价划分的平等性，故定理 1 中出现的H(D),HC(A|D)分别对称于定义1 中的H(A),HC(D|A)；进而，定理1 提供5 种互补信息度量的系统方程。定理2 则表明互补信息系统具有粒化单调性，其中的粒化关系U/IND(A)≥U/IND(B)可由A⊆B实现。

邻域粗糙集是经典粗糙集的拓展，其基础为邻域系统[16,21]。对决策表DT，设A={c1,…,cn}⊆C，则其对应距离函数可以诱导邻域关系NRA={(x,y)∈U×与邻域覆盖表示n个邻域。

定理 3[16,21](1)若δ1≤δ2, 则 ∀x∈U有若δ=0, 则(x)=[x]A。 (2)若A⊆B,则 ∀x∈U有(x)(此时也记U/NRA≥U/NRB)。

邻域依托其覆盖结构为邻域粗糙集奠定了粒计算基础。基于定理3，邻域具有参数单调性，δ=0导致退化，即邻域粒退化到等价类且邻域粗糙集退化到经典粗糙集；此外，邻域还具有关于属性子集关系的单调性，这为相关粒化单调性奠定了基础。

2 邻域互补信息度量及其性质

经典互补信息度量[6,8]适用于经典粗糙集。针对扩张的邻域粗糙集，本节自然定义邻域互补信息度量, 以实施度量扩张与拓展应用。下面主要针对决策表DT及其邻域覆盖U/NRA={(x)i|i∈ 1,…,n}与决策分类U/IND(D)={Dj|j∈ 1,…,m}。

2.1 邻域互补信息度量

定义2A⊆C的邻域互补熵、D关于A的邻域互补条件熵、A与D之间的邻域互补互信息分别为本文采用p=1 的Manhattan 距离函数。加上半径参数δ，则x的领域

定理4若δ=0，则NHδ(A)=H(A),NHCδ(D|A)=HC(D|A),NMIδ(D;A)=MI(D;A)。

定义2 的邻域互补信息度量模拟了定义1 的经典互补信息度量，主要将知识划分U/IND(A)拓展替换为邻域覆盖U/NRA(即等价类换为邻域(x)i。这种基于解析式的拓展方案，比较自然也更为稳妥。由此，邻域互补信息度量具有扩张性(定理4)。3 种邻域度量具有类似于经典互补熵的不确定性语义，但代替地使用邻域覆盖结构。为了有利于邻域覆盖结构的近似推理，它们具体采用邻域粒不重复计数机制，这区别于元素诱导的邻域可重复机制[16]。此外，定义2 也提供了补集描述与等价本质两种形式。下面模拟确定NHδ(A)，NHCδ(D|A)的对称度量NHδ(D)A，NHCδ(A|D)，并发展系统关系。

命题1邻域互补熵具有等价“双和形式”

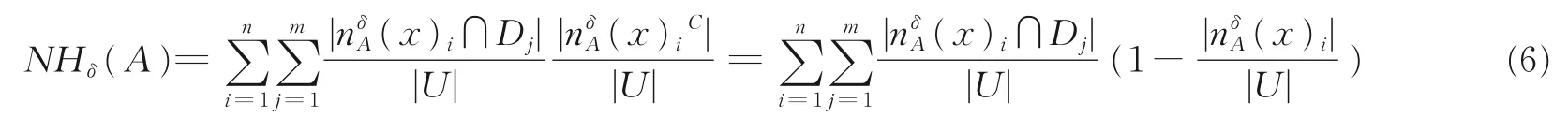
证明由式(5)与U/IND(D)的剖分性有

命题2，若δ=0 时等号成立。

证明由式(3)与U/NRA的覆盖性，类似于命题1 的证明过程有

其中覆盖U/NRA退化为划分U/IND(A)时(此时δ=0)，上述等号成立。

定理5 采用类似于NHδ(A)(式(6))与NHCδ(D|A)(式(5))的“双和形式”，设置符号

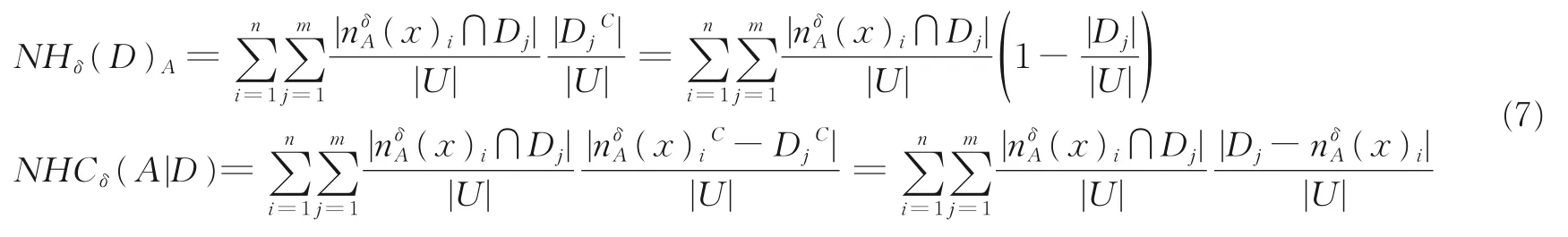
则邻域互补熵、邻域互补条件熵和邻域互补互信息满足如下系统方程

证明(1)注意到具有两剖分部分由式(6，7)有

(2)由式(6，7)有

命题1 提供邻域互补熵NHδ(A)的“双和形式”。命题2 涉及的“双和形式”类似且对称于NHδ(A)的，但其不同于且不小于H(D)，这是因为覆盖U/NRA替换了划分U/IND(A)。由此，定理5 提取命题2“双和形式”形成新符号NHδ(D)A，其依赖于A从而区别于只依赖于D的H(D)；此外，定理5 还提供了NHCδ(A|D)。可见，NHδ(D)A与NHδ(A)具有在“双和层面"的粒交换性，而NHCδ(A|D)与NHCδ(D|A)具有集差换序。从而，定理5 证明并表现了邻域互补信息度量的系统关系，其对应经典互补信息度量的系统关系(式(2))。由此，下述推论1 补充了NHδ(D)A,NHCδ(A|D)对于H(D),HC(A|D)的扩张性，还揭示了NMIδ(D;A)≠H(D)-NHCδ(D|A)的扩张特异性。由此定理所述0 值条件容易检验。

推论1(1)若δ=0,则NHδ(D)A=H(D),NHCδ(A|D)=HC(A|D)。

(2)NHδ(D)A≥H(D),NMI(D;A)≥H(D)-NHCδ(D|A)，若δ=0 时等号成立。

定理 6U/NRA≼U/IND(D)(即的充分必要条件是NHCδ(D|A)=0。

证明(1)若U/NRA≼U/IND(D),则即有因此由式 (5)有NHCδ(D|A)=0。 (2)反设NHCδ(D|A)=0,但U/NRA⋠U/IND(D)。此时，∃i*∈{1,…,n}，j*∈因此 , 由式 (5)有该矛盾意味着充分性成立。

推论 2U/NRA≼U/IND(D)等价于NMIδ(D;A)=NHδ(D)A,NHδ(A)=NHCδ(A|D)+NHδ(D)A。

定理7(1)NHδ(A)∈[0,|U|/4]，且U/NRA={U}⇒NHδ(A)=0。

(2)NHCδ(D|A)∈[0,|U|],且U/NRA≼U/IND(D)⇒NHCδ(D|A)=0。

(3)NMIδ(D;A)∈[0,|U|],且U/NRA={U}⇒NMIδ(D;A)=0。

证明(1)0 是显然的，且可由U/NRA={U}取得。

(2)由式(5)有

由此定理所述0 值条件容易检验。

推论3H(A),HC(D|A),MI(D;A)都具有双界范围[0,1]。

表1 实例决策表Table 1 Instance decision table

2.2 邻域互补信息度量的粒化非单调性

不确定性度量的粒化单调性或非单调性是信息应用的一个重要特性[2,3,15]，决定着属性约简的定义构造与算法启发。定理2 表明，经典互补信息度量具有粒化单调性。本小节阐述邻域互补信息度量基于扩张变异的粒化非单调性。下面首先通过一个实例来计算信息值并提供非单调事实。

例 1决策表DT如表 1，其中U/IND(D)={D1={x1,x2,x4,x5},D2={x3,x6,x7}}。

基于Manhattan 距离与半径δ=0.5，可以构建邻域体系。为了研究粒化，下面聚焦自然属性增链：{c1}⊂{c1,c2}⊂{c1,c2,c3}⊂{c1,c2,c3,c4}⊂{c1,c2,c3,c4,c5}(链元属性集用A统一表示)。表2 提供相关邻域及覆盖。再由式(5，7)，表3 提供所有5 种邻域互补信息度量值。作为例子，链元{c1,c2,c3}的前3 个度量计算过程为：

表2 基于属性增链的邻域及覆盖Table 2 Neighborhood and coverage based on attribute chaining

表3 基于属性增链的邻域互补信息度量Table 3 Neighborhood complementary information metric based on attribute chaining

基于表3 结果，首先可以检验系统式(8)，即表3 中第(3)个度量值等于第(4)与(2)的度量值的差，也等于第(1)与(5)的度量值的差。此外当A取 {c1,c2}或{c1,c2,c3}时不等号为严格大于;可见，NHδ(D)A依赖于A从而不同于只依赖于D的常值H(D)，进而NMIδ(D;A)≠H(D)-NHCδ(D|A)(推论1)。最后聚焦粒化非单调性。伴随属性增链的覆盖细化，这5 种度量都呈现“先增大后减少”趋势，该波动充分说明了所有度量的粒化非单调性。关于属性增链，虽然单元素具有邻域细化(即 ∀x∈U有但覆盖在“脱离元素追踪”与“去除粒重复”后呈现对应变化的复杂性，比如覆盖粒数具有波动：|U/NR{c1}|=1＜|U/NR{c1,c2}|=5 ＜|U/NR{c1,c2,c3}|=6 ＞ |U/NR{c1,c2,c3,c4}|=5 ＜ |U/NRC|=7。

定理8设U/NRA≽U/NRB，则同类型的邻域互补信息度量在A与B上的大小关系是不确定的，即以下5 组度量无必然的大小关系：

(1)NHδ(A)与NHδ(B)；(2)NHCδ(D|A)与NHCδ(D|B)；(3)NMIδ(D;A)与NMIδ(D;B)；(4)NHδ(D)A与NHδ(D)B；(5)NHCδ(A|D)与NHCδ(B|D)。

基于例1 的事实支撑，定理8 自然提供5 种邻域互补信息度量的粒化非单调性。主要分析前面3 种重要度量的相关机制。事实上，度量的覆盖刻画具有对分类刻画的拓展性并利于后续近似推理，但直接的邻域粒变化具有复杂性，这在很大程度上诱导了相关的粒化不确定性。

(1)基于式(5)，邻域互补熵的“单和内部”涉及上凸抛物函数p(1-p)，其先增后减并在p=0.5 处取得最大值 0.25。当U/NRA≽U/NRB时，有(x)( 定理 3)，因此 ∀x∈U有但无法确定p((x)))的大小关系。后续覆盖细化也具有不确定性，因此NHδ(A)与NHδ(B)无必然大小关系。

(2)类似地,当U/NRA≽U/NRB时,领域互补条件熵“双和内部”具有信息减少的确定趋势：但在后续求和中信息具有增加的可能性，因为B的邻域粒数可以更多。最终，NHCδ(D|B)对比NHCδ(D|A)的大小关系还是无法确定。

(3)当U/NRA≽U/NRB时,领域互补互信息的“双和内部”具有与这两种相反方向的确定性导致两种因子乘积大小的不确定性。此外,“双求和”粒数目仍然是一个不确定问题，因此也无法最终确定NMIδ(D;A)与NMIδ(D;B)的大小关系。

3 基于邻域互补互信息的启发式属性约简

基于相关的不确定性语义，邻域互补熵和邻域互补条件熵、邻域互补互信息都可以被利用于属性约简构建。针对决策表，考虑到邻域互信息能够有效度量从条件属性到决策属性的信息量与依赖度，故本节主要采用该测度来构建启发式属性约简。基于粒化非单调性(定理8)，这里采用文献[15]的约简策略与算法思路，其主要追求更高互信息量。

定义3基于决策表DT，R⊆C称为C的一个约简，若(1)NMIδ(D；R)≥NMIδ(D；C);(2)∀r∈R，NMIδ(D;R-{r})＜NMIδ(D;R)。

定义4属性a∈A,a∈(C-A)关于A的内部、外部重要度分别为sigin(a,A,D)=NMIδ(D;A)-NMIδ(D;A-{a})；sigout(a,A,D)=NMIδ(D;A∪{a})-NMIδ(D;A)。

这里的约简追求更优的邻域互补互信息，定义3 中的两条分别描述相关的“联合充分性”与“独立必要性”。内重要度sigin(a,A,D)表示在A中删除属性a产生的关于邻域互补互信息的信息减量，而外重要度sigout(a,A,D)表征在A上增加属性a产生的信息增量，两者提供了快速约简的属性选择机制。若NMIδ(D;C-{c})＜NMIδ(D;C)，此时有 sigin(c,C,D)＞ 0，即c关于C是重要的，因此可以构建C的重要属性子集。类似地，sigout(a,R,D)＞0 说明a关于R是重要的，因此可以选择最大外重要度的对应属性加入R以实施快速更新。下面采用这两种重要度来设计一个启发式搜索算法，以快速得到一个约简。

算法1基于邻域互补互信息的属性约简启发算法

输入决策表DT、邻域半径δ;

输出基于邻域互补互信息的属性约简R。

Step 1设置R=∅；

Step 2∀ci∈C，计算 sigin(ci,C,D)，若 sigin(ci,C,D)＞ 0，则实施更新R←R∪{ci}；

Step 3计算邻域互补互信息NMIδ(D;R)与NMIδ(D;C)，若NMIδ(D;R)≥NMIδ(D;C)，则进入第5 步，否则进入第4 步；

Step 4∀a∈(C-R)，计算 sigout(a,R,D)，并选择外部属性重要度最大的属性a∗，进行更新R←R∪{a∗}，并进入步骤 3；

Step 5∀ri∈R，若NMIδ(D;R-{ri})≥NMIδ(D;R)，则进行更新R←R-{ri}；

Step 6返回R。

算法1 优化了文献[15]的非单调算法结构，并主要采用邻域互补互信息及其属性重要度进行启发式快速搜索。步骤1 进行初始化。步骤2 基于内重要度启发，搜索C中所有重要属性并循环加入R。步骤3 是1 个评估过程,若R不满足约简第1 条，则进入步骤4，选取最大外重要度的属性进行快速的循环更新；(最终)满足第1 条,再利用步骤3 进入步骤5。步骤5 循环删除冗余属性。由此，步骤6 输出结果。该算法能够快速得到一个基于邻域互补互信息的属性约简，相关时间复杂度是可行的[15]。

例2基于例1 的决策表及相关设置与计算，下面说明算法1 及其有效性。具体地，步骤1 赋值R=∅。步骤2 计算C种属性的内重要度

由此,将{c1,c3,c4,c5}4 个重要属性循环添加到R中，此时R更新为R={c1,c3,c4,c5}。步骤3 计算有

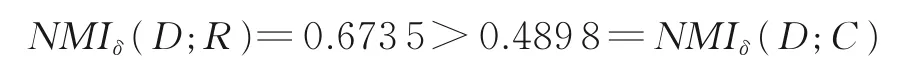
满足约简条件1，故进入步骤5。步骤5 实施反向冗余剔除。由

故R剔除c3,保留c1,c4,c5。且R更新为R={c1,c4,c5}。由

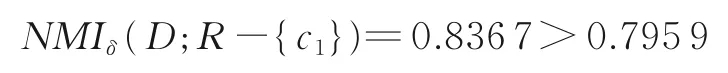
故剔除c1,保留c4,c5。且R更新为R={c4,c5}。由

此时，步骤6 输出最终约简结果R={c4,c5}。

4 UCI 数据实验

本节实施数据实验来验证邻域互补熵、邻域互补条件熵和邻域互补互信息的粒化非单调性，以及基于邻域互信息的启发约简算法1。具体从UCI 机器学习数据库（http：//archive.ics.uci.edu/ml）选取5 类数据集(如表4)。首先采用最大-最小标准化数据预处理，仍用Manhattan 距离函数，邻域半径参见表4。

表4 5 类UCI 数据集描述Table 4 Description of five categories of UCI data sets

为揭示信息变化，选取自然属性增链{c1}⊂{c1,c2}⊂…⊂C(设链元{c1,…,ck}=(Ak))。针对核心度量NHδ(Ak),NHCδ(D|Ak),NMIδ(D;Ak)，表 5 提供了截断于A13的主体信息值，图 1 则进行全部数值描绘(其横坐标对应Ak的k，3 种度量简记为NH,NHC,NMI)。基于表 5 分析，结合图 1 趋势，3 种度量的粒化非单调性均非常明显，对于基于邻域互补互信息的启发式属性约简，算法1 提供如下有效约简结果(表 6 左栏)。

表5 5 类数据集关于属性增链的3 种邻域互补信息值Table 5 Three kinds of neighborhood complementary information values for attribute chaining with five categories of data sets

图1 5 类UCI 数据集关于属性增链的3 种邻域互补信息的非单调变化Fig.1 Non-monotonic changes in complementary information of three neighborhoods of attribute-added chain in five categories of UCI data sets

本文度量与算法最相关于文献[15]，为了相关对比，补充了文献[15]的信息熵值及算法的数据实验,仍然基于表4 的5 类数据集。基于相关实验结果,文献[15]基于属性增链的3 种度量值结果与表5 的差距不大,对应的非单调图与图1 也类似，故两者都省略。文献[15]算法所得约简结果放入表6 右栏，其与本文算法1 的结果(表6 左栏)具有较明显的差异性；此外，文献[15]算法的实验处理比算法1 需要更多的时间。综上实验结果对比可见，两套信息度量值具有一定的相似性，但启发的约简结果具有差异性，如表5(a)中{c1,c2,c6,c9}≠{c1,c2,c3,c9}等，这种相关性与差异性来源于两者的度量机制。基于相关分析,两套度量具有相同的外部“叠加求和”，在这种多信息融合情况下，内部的p(1-p)与-不能导致宏观显著性的值差异。但是这两种度量的微观差异在算法中会发生作用,从而致使启发属性的选择与顺序，即两种度量具有不同的约简启发性，故两者算法结果有所不同。此外，本文算法1 对文献[15]算法的反向冗余剔除模块进行了结构改进，此实验中自然具有更高效率。

表6 两种算法下的约简结果Table 6 Reduction results under two algorithms

5 结束语

基于解析式模拟与粒替换，本文将经典粗糙集的经典互补信息度量推广到邻域粗糙集的邻域互补信息度量，得到了相似的系统体系(其中H(D)被NHδ(D)A所替代)，并将粒化单调性拓展为粒化非单调性，同时还得到了关于退化与双界等性质。基于邻域互补互信息及其粒化非单调性，提出属性约简及其启发式算法。最后，相关实例与实验都验证了研究结果的有效性。邻域互补信息度量及其属性约简还值得深入研究与应用，例如可以构建基于邻域互补(条件)熵的属性约简进行系统研究与应用。