遗传算法求解带权重的生产调度问题*

王召阳 高 尚

（江苏科技大学计算机学院 镇江 212001）

1 引言

车间调度是现代企业制造的基础，优化生产调度是先进企业亟需解决的关键问题。在实际生产过程中，工件一般都是按批生产的，所以研究批量调度的优化方法对现代企业有着重要的实际意义和理论价值。生产排程问题又称生产调度或生产计划，于1954年由S.M.Johnson首先提出，并建立了加工的数学模型，同时提出了优化算法。60年代普通的优化方法开始用于解决实际调度问题。70年代着重于问题复杂性方面的研究。80年代初，调度理论结合实际生产成为研究的主要问题［1］。国内生产调度研究起步于20世纪90年代，比国外起步要晚。随着生产调度方法的广泛应用，目前国内调度算法的研究已日趋完善，研究的主要方向也不再仅仅局限于调度理论，而是把理论与实际相结合，考虑到了车间问题的复杂性和多约束性。目前国内研究的生产调度大多把加工时间混合考虑，只注重生产周期最短，忽略了工件加工的排队时间和运输时间［2］。

本文针对目前的研究现状，将加工时间、运输时间和排队时间相分离，结合不同的时间权重，找出适合的生产排程组合，同时将遗传算法的选择算子和变异算子进行改进，得出针对实际问题的可行解。最后通过仿真结果给出不同时间权重对应的收敛图。

2 批量生产调度问题描述

结合车间生产的实际情况，批量调度问题可描述为：有N种工件，每种工件有多个并且包含多道工序，有M台机床，能加工某一种工序的机床有多台，每道工序在不同机床加工的时间不同。问如何分配工件的加工顺序，使得工件的总加工周期最小［3～4］。同时该问题还包含以下约束条件：

1）某台机器加工某一工序的时间是确定的；

2）同一工件加工的工序顺序是确定的；

3）同一工件的一道工序可在不同机器上加工；

4）不同工件的加工工序没有先后顺序约束；

5）生产周期分为加工时间、排队时间和运输时间；

6）同种工件即为最小批次，不可分批；

7）每台机床同一时间只可加工一种工件；

8）加工中的工件不可中断；

9）在开始时刻，所有的工件都可被加工。

3 批量生产调度策略

根据问题描述，建立以下调度模型：在调度系统中，共有13台加工机器，6种工件，每种工件的批次数量都不相同，每种工件在各个机器上的加工时间也不相同，工序的批次启动时间即为单个工件此工序的开始时间。

3.1 工件加工工序

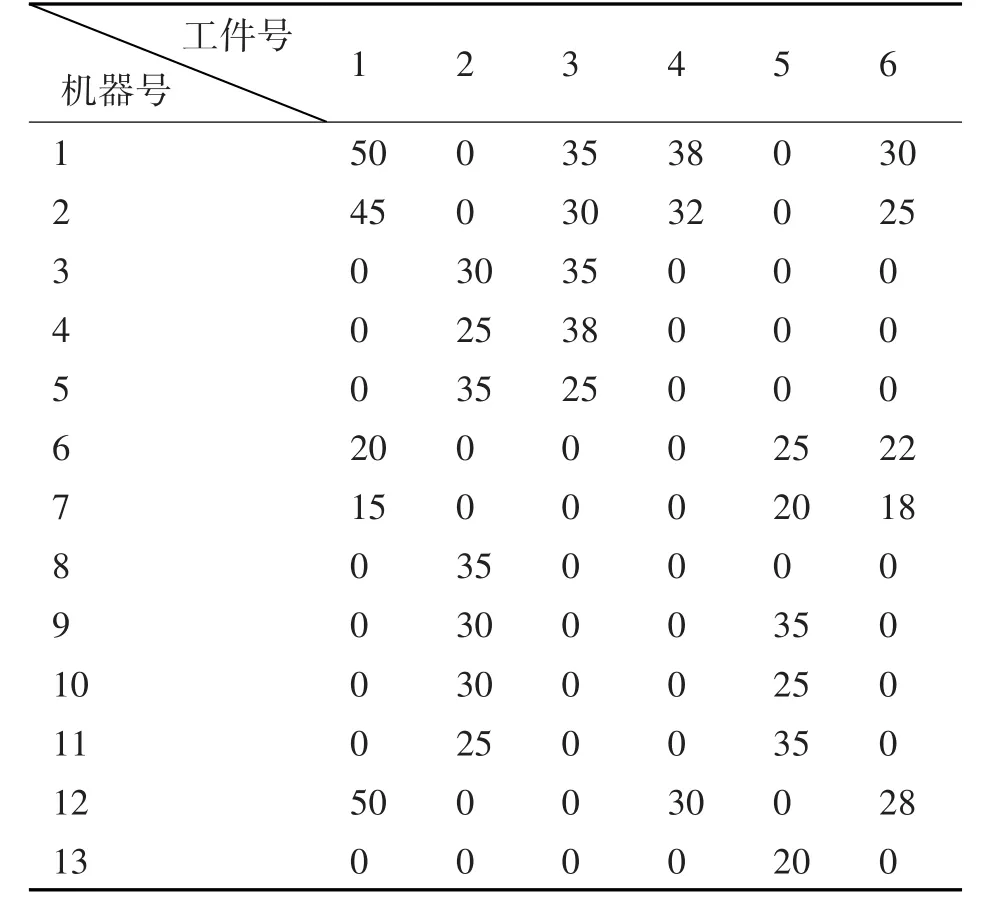
表1 工件在机器上的加工时间

表1为6种工件对应于13个机器的加工时间，为简化模型，现假设每种工件最多只有3种工序，依据表1，得出每种工件的工序顺序如下：

工件1：8种加工顺序，对应的机器号分别为2-7-11， 1-7-11， 2-6-11， 1-6-11， 2-7-12，1-7-12，2-6-12，1-6-12；

工件2：8种加工顺序，对应的机器号分别为4-9-0，3-9-0，4-8-0，5-9-0，4-10-0，3-8-0，5-10-0，5-8-0；

工件3：6种加工顺序，对应的机器号分别为2-3-0，2-4-0，2-5-0，1-3-0，1-4-0，1-5-0；

工件4：4种加工顺序，对应的机器号分别为2-11-0，1-11-0，2-12-0，1-12-0；

工件5：6种加工顺序，对应的机器号分别为13-7-9， 13-6-9， 13-7-8， 13-7-10， 13-6-8，13-6-10；

工件6：8种加工顺序，对应的机器号分别为7-2-11， 6-2-11， 7-2-12， 7-1-11， 6-2-12，6-1-11，7-1-12，6-1-12。

3.2 工件加工时间

在实际生产过程中，工件在机器上的加工是需要装卸工件和启动机器的，这些时间可以算在加工时间内，但机器和机器间的运输距离无法忽略，以及同一机器加工不同工件的等待时间也需考虑在内，机器间的距离如表2。

3.3 工件加工时间与等待时间

一台机器加工两种零件，后一种零件就需要排队等待；不同机器加工同一零件的不同工序，后一台机器就需要等待零件的前一工序加工完成，同时机器和机器间还存在运输时间，因此加工时间和排队时间共分为五种情况。

现说明定义的各个变量：

tij：工序j在机器i上的加工完成时间；

TTdej-1：工序j的紧前工序j-1在机器de上的批次加工时间；

TTij：工序j在机器i上的批次加工时间；

tranij：加工工序j运送到机器i上的运输时间；

wij：工序j在机器i上的排队时间。

情况一：若待加工工件无紧前工序且加工机器无工件加工，如图1。

情况二：若待加工工件无紧前工序且加工机器

表2 机器间的运输时间

有工件加工，如图2。

图1 加工示意图

图2 加工示意图

情况三：若待加工工件有紧前工序且待加工工件的紧前工序所用时间大于当前机器加工前一种工件的加工时间，如图3。

图3 加工示意图

情况四：若待加工工件有紧前工序且待加工工件的紧前工序所用时间小于当前机器加工前一种工件的加工时间，待加工工件的运输时间与工件等待时间重合，如图4。

图4 加工示意图

情况五：若待加工工件有紧前工序且待加工工件的紧前工序所用时间小于当前机器加工前一种工件的加工时间，待加工工件的运输时间与工件等待时间部分重合，如图5。

图5 加工示意图

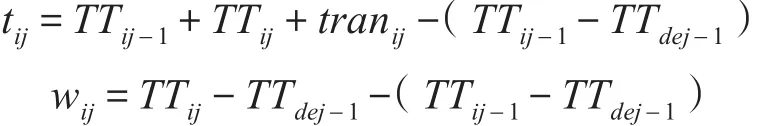
4 批量生产调度的加权遗传算法

4.1 遗传算法的基本思想

遗传算法从可能代表问题潜在解集的一个种群开始，一个种群由包含基因特征的染色体组成，染色体是经过编码的从性状到基因的映射。初始种群按照优胜劣汰的原则，根据适应度大小挑选若干个体，通过交叉、变异，产生符合问题解的新的个体，再从中挑选种群数量的个体的一系列遗传操作。经过多次操作，最终得出问题的近优解或最优解［5］。

交叉运算：双亲染色体部分基因相互交换重组，产生新的符合问题解的个体。

变异运算：改变父代染色体的部分基因，产生新的符合问题解的个体。

选择运算：根据各个染色体适应度大小，选择适应度高的个体进入下一代。

遗传算法的步骤［6］如下。

1）根据问题，随机产生符合问题解的初始种群，产生的个体数目确定，每个个体表现为染色体的基因编码；

2）根据每个个体的适应度判断是否符合优化标准，若符合，输出最优解；若不符合，转第3）；

3）由交叉概率和交叉算子产生新的个体；

4）由变异概率和变异算子产生新的个体；

5）通过选择算子和选择方法，挑选出种群数量的优化个体，返回第2）。

遗传算法的特点［7～8］如下。

1）遗传算法是将自然选择和种群遗传简单化后的超启发式算法；

2）采用概率化的搜索方法，不需要确定的规则，只需要设定正确的适应度函数即可；

3）遗传算法从问题的串集开始，同时处理多个个体，覆盖面广，不容易陷入局部最优，可以评估搜索空间多个解，实现并行求解，效率更高；

4）适应度函数不受连续可微的影响，并且可以任意设定定义域，使得遗传算法的应用范围更广；

5）通过选择算子、交叉算子和变异算子指导遗传算法的搜索方向，适当的设定交叉概率和变异概率，可以避免算法陷入局部最优，利于全局寻优；

6）搜索方向并不是无序的，它是有序的搜索，这就决定了遗传算法比传统搜索算法有更高的搜索效率；

7）遗传算法可以方便结合其他算法或对其进行适当改进，针对具体问题可以更快更准确地求出最优解。

基于遗传算法的诸多特点，多工序的批次生产调度问题就可以很方便地使用遗传算法进行求解。根据车间调度的实际问题，改进传统遗传算法的遗传算子，使其适用于具体问题的最优化求解［9］。

4.2 批量调度遗传算法

生产调度实现算法决定着生产调度问题的可行性，根据实际问题，需要对遗传算法进行适当的改进，确定初始种群为5，迭代次数为100，个体长度为12。

编码：这里采用10进制编码，个体长度定为12，前6位代表6种工件序号，每位不可重复，后6位代表对应的工件的加工顺序，每位可重复。

根据3.1的加工工序，工件1有8种加工顺序，工件2有8种加工顺序，工件3有6种加工顺序，工件4有4种加工顺序，工件5有6种加工顺序，工件6有8种加工顺序。

染色体为635124354824。

工件对应的加工顺序为 6-3，3-5，5-4，1-8，2-2，4-4。

第一次转换：每个个体采用6行3列矩阵表示，根据初始群体，每行代表对应的工件种类，每列代表加工的顺序所用的机器号。

第二次转换：每个个体采用13行18列矩阵表示，根据第一次转换结果，每行代表1-13的机器号，每列代表机器号加工的工件种类序号，由此就可详细表示出每个机器加工各个工件种类对应的各个工序排列。

选择算子：采用锦标赛选择法，随机抽取若干染色体，取适应度高的个体进入下一代，重复此方法，直到选到足够多的个体为止。

交叉算子：先选择两个染色体作为双亲染色体。

S1：635124354824

S2：452361366178

前6位随机产生两个交叉点2和4，后6位也随机产生两个交叉点8和10，如果根据传统遗传算法，交叉后结果为

S11：652324366124

S22：435161354878

产生的后代S11前6位就存在两个相同工件2，后6位存在工件不存在的加工顺序；S22前6位存在相同工件1，后6位也存在工件不存在的加工顺序，都是问题的不可行解。所以需要改进传统遗传算法的交叉算子，本文采用多点交叉和改进的交叉算子相结合的方法［10］。

每一个染色体中不可存在相同的工件种类，同时工件种类的加工顺序必须在对应的加工顺序中。以上两个染色体为例，假设交叉点为2、4、8、10，则两个染色体对应的2-4之间的基因段互相放入对方染色体之前，同时检查前9位，删除重复出现的基因位，留下6位。8-10对应的基因段分别互换，检查后6位对应的加工工件种类，若超出加工的顺序序号，则取序号的最大值为此工件的加工顺序。

S11：523614366124

S22：351426344478

具体操作步骤如下。

1）取种群中两个染色体作为双亲染色体；

2）随机产生1-6之间的两个整数a和b和7-12之间的两个整数c和d；

3）将两个染色体对应的a-b之间的基因段分别放在染色体之前，删除各个染色体原本前6位中重复a-b段的基因；

4）将两个染色体对应c-d之间的基因段互换，同时检查前6位对应的工件种类的工序顺序号是否超出最大值，若超出，以最大值替换。

按此交叉方法得到的染色体都是可行解，确保了所有个体都是合法个体。

变异算子：选择一个染色体作为父代染色体。

S1：523614366124

前6位产生一个变异点3，后6位产生一个变异点12，根据传统遗传算法，变异结果为

S11：526614366128

产生的后代S11前6位就存在两个相同工件6，后6位就存在工件4没有的加工顺序8，产生的个体为问题的不可行解。所以需要改进传统遗传算法的变异算子，本文采用移位变异和交叉基因位相结合的方法。

每一个染色体中不可存在相同的工件种类，同时工件种类的加工顺序必须在对应的加工顺序中。以此染色体为例，假设变异点为3和5，则对应的后6位的变异点为9和11，同时互换3和5、9和11位对应的基因［11～12］。

S11：521634362164

具体操作步骤如下：

1）取种群中的一个染色体作为父代染色体；

2）随机产生1-6之间的两个整数a和b，同时取后6位对应的整数a+6，b+6；

3）将染色体a和b对应的基因位以及a+6，b+6对应的基因位互换，得到新的个体。

按此变异方法得到的染色体都是可行解，确保了所有个体都是合法个体［13］。

适应度函数是评价种群个体优劣程度的依据，它给定了解的搜索方向并直接关系到搜索过程的效率和最终解的质量。若适应度函数设定不当，将是搜索过程变得复杂，解的质量也会大打折扣［14～15］。

本文设定的适应度函数：总的生产周期等于总最大加工时间、总的加权排队时间以及总的加权运输时间之和。综合考虑了所有工件在机器加工完成的最终时间最小，同时所有工件排队时间最小以及所有工件运输时间最小。

适应度函数：

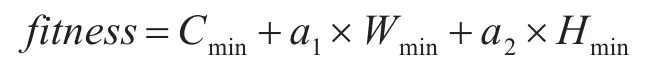
Cmin为最后一台完工机器的加工时间；

a1×Wmin为工件总排队时间的加权值；

a2×Hmin为工件总运输时间的加权值。

4.3 批量调度遗传算法流程

流程图6详细说明了批次调度的详细步骤，适应度函数采用加权值，通过改进的交叉操作和变异操作，最终得到最优个体。

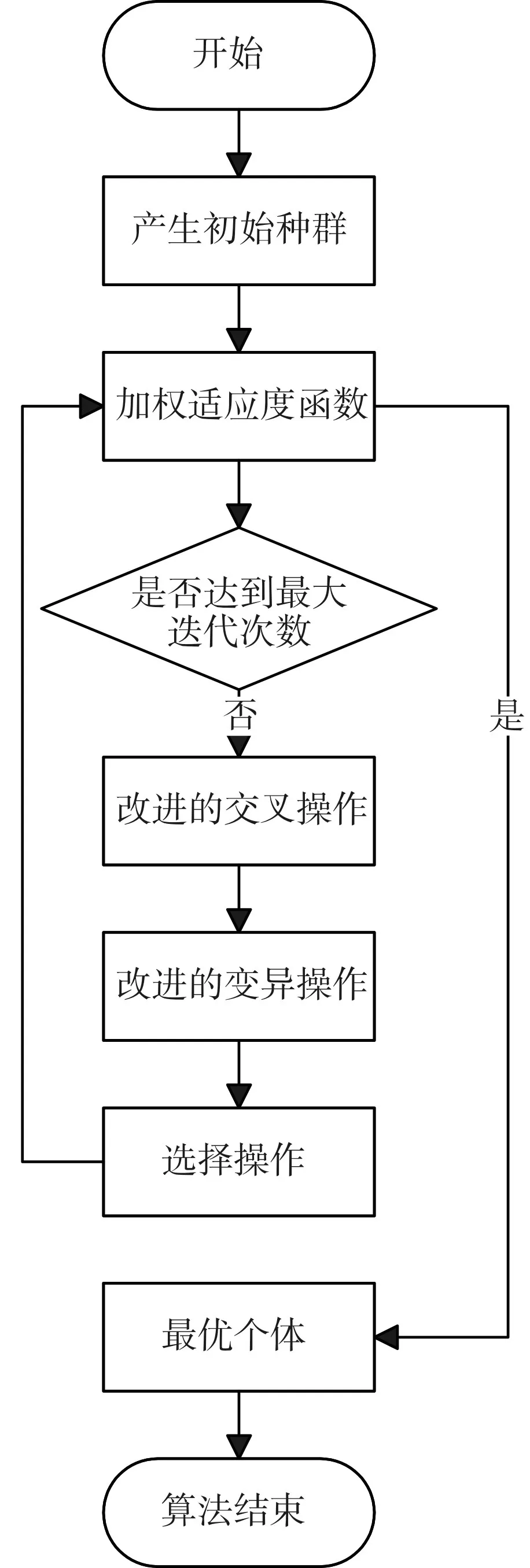
图6 批次调度加权遗传算法的流程图

5 仿真结果和分析

仿真模型使用实际数据进行模拟，设一共有13台机器，共6种工件，每种工件批次为5、15、12、6、10、3，每种工件最多3道工序，机器加工时间为表1，机器间运输时间为表2，染色体长度为12，采用10进制编码。种群规模为10，同时对应5种权值，加快遗传算法的运行速度。迭代次数为100，交叉概率为0.6，设置过小会抑制种群生成新个体的速度，容易陷入局部最优，过大会破坏种群中的优良个体，使搜索趋于无序化；变异概率为0.001，过小会抑制产生新个体的能力，过大会破坏产生的优良个体。仿真结果如下。

横坐标表示迭代次数，纵坐标表示每代的最小生产周期。

批量生产调度加权算法的各个权值优化结果为

排队权值1，运输权值0：425316416121；

排队权值0.75，运输权值0.25：425361423334；

排队权值0.5，运输权值0.5：534261414522；

排队权值0.25，运输权值0.75：534612514225；

排队权值0，运输权值1：453261231552。

如图7所示，总的生产周期在极小概率会相同，大部分情况如图8所示。

图7 批次调度加权遗传算法收敛图

图8 批次调度加权遗传算法收敛图

此时的批量生产调度加权算法的各个权值优化结果为

排队权值1，运输权值0：463215213163；

排队权值0.75，运输权值0.25：654321142312；

排队权值0.5，运输权值0.5：543621621316；

排队权值0.25，运输权值0.75：432561432452；

排队权值0，运输权值1：543621541158。

通过多次仿真结果分析和研究表明，当机器间没有运输距离时，也即运输权重为0时，生产周期为所有周期中最小；当运输权值增大时，总生产周期也在慢慢变大，当排队时间权重和运输时间权重以及工件生产顺序达到一个平衡时，可以接近最小生产周期；即使不同的加工次序，当机器的运输权重和排队权重互相协调时，也可能会有相同的生产周期，这就需要企业针对本厂的工件批次和工件加工顺序，合理安排排队权重和运输权重，以期得到最小的生产周期。

6 结语

系统研究了多工序的批量生产调度问题，主要着重于批次生产的时间总和问题，将总的生产周期分为加工时间、排队时间和运输时间，运用不同的时间权重，结合改进的遗传算法的编码方式、改进的交叉算子和改进的变异算子，通过加权的适应度函数，给出了各个不同时间权重下的总生产周期。仿真结果表明，工件的不同顺序结合适当的时间权重可得出更小的生产周期，改进的遗传算法使搜索性能大大提升，确保了解的合理性、准确性。