基于灰度预测的灾难医学救援培训研究*
2020-08-11李雪菁韩朝阳窦粲灿汤璐佳潘曙明
李雪菁 陈 瑛 韩朝阳 窦粲灿 汤璐佳 潘曙明
(1.上海杉达学院信息科学与技术学院 上海 201209)
(2.上海交通大学医学院附属新华医院急诊医学科 上海 200092)
(3.上海大学机电工程与自动化学院 上海 200072)
1 引言
世界范围内各类灾难频发直接威胁着人类的生存和发展。据国际灾难数据库不完全统计,1900年至今,我国发生各种重大自然灾害700余起,受灾人数超过25亿,经济损失超过3400万亿美元[1]。在任何社会环境中,任何历史时期,灾难医学救援体系关系到国家发展,社会安定。灾难一旦发生,势必会有人员伤亡,需要立刻组织应急响应人员尤其是医务人员进行应急响应,这就要求医院要有应对紧急状况的能力储备,相关医务人员需要进行灾难培训及提高团队全方位的应对能力。如何有效应对大规模灾难,这引起了各国研究学者们的重视。教育与培训是灾难应急准备与计划的必不可少的一部分,教育与培训的质量至关重要[2~3]。当前国际上对灾难医学的研究和实践日渐深入,对医学生灾难医学教育和救援能力培养进行了很多实践探索[4~6]。近期发生的自然灾害与大规模人员伤亡事件的应急响应程序表明灾难应急响应人员尤其是医务人员日常灾难应急响应能力训练十分重要[7~9]。灾难发生后的数小时以及数天内造成的死伤人数将达到高峰,因此医务人员的快速反应尤其是对危重伤患的合理处置对于灾难应急响应的结果影响重大[10~12]。美国具有较完善的应急救援体系,同时非常重视灾难医学救援培训。1990年,(美国)国家灾难生命支持课程(National Disaster Life Support,NDLS)立项,该课程主要包括:灾难救援基本程序、基本技术、伤员检伤分类、灾区传染病的预防和处理、灾难心理救援等[13~16]。2015年由新华医院参与引进该培训课程。引入的NDLS培训课程在应急协调等方面具有一定的优势,但原版课程毕竟是基于美国国情,如何更好地发挥该培训课程的优势,需要增加符合我国国情的案例,针对以上问题,本研究对目前培训效果进行了详细分析,并根据培训学员成绩的灰色预测,评估培训课程,为动态调节课程教案并增加案例提供依据,以保证培训课程体系适应中国国情的动态发展。本研究结果也可作为同类培训相关研究依据。
2 灾难医疗培训课程体系
我国灾难医学救援的核心力量主要依靠各级医院,因此基层医疗机构人员的灾难救援能力的培训是非常关键的,NDLS培训课程是针对医疗行业的工作人员,比如医生、护士等。课程培训体系见图1。

图1 灾难医疗培训课程体系
1)课前问卷
为了能够更好地对采集数据进行分析及挖掘等课前问卷包括性别、年龄、教育程度、职业、救灾经历、对灾难救援培训的态度等。为了保证数据提取的可靠性及有效性学员被要求独立完成且课前题作答系统在培训开始前关闭。
2)培训课程
培训课程分为理论部分及实践两部分。理论部分课程涉及到灾难医学的大部分内容,概括为公共卫生(包括准备、部署、统筹等)、各类型的灾难、洗消与个人防护、法律法规等。在实践部分,采用的是综合模拟形式,即将理论培训的知识要点融入综合演练中。
3)课后问卷
课后问卷包括两部分:针对培训内容的医学类理论知识考核及对培训导师的教学方法的意见,比如授课方法、组织安排满意度等。对于不同的业务,其可能提供不同的信息。通常不同的业务对信息需求的侧重点不同,因此数据需要与其他管理直接相关的信息,同时也需要其他大量的辅助信息。
3 数据来源及现阶段培训效果分析
本研究所分析的数据来源为参训NDLS的388人信息。对目前采集信息进行分析处理,结果如图2-7所示。

图2 培训学员分布城市

图3 学员年龄分布

图4 学员性别分布
4 灰度预测模型建立
对于培训效果的监测和预测是本研究的关键。培训效果的精确预测对及时调整培训模式及引入新的教学实例均有积极意义。本研究采用定量预测,运用对参加培训学员的测试情况的数据统计分析,对今后测试情况的发展水平做出数量的说明。
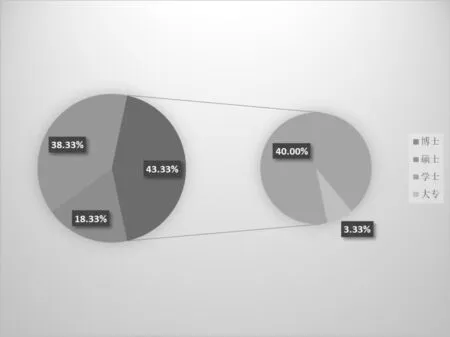
图5 学员学历分布

图6 学员专业分布
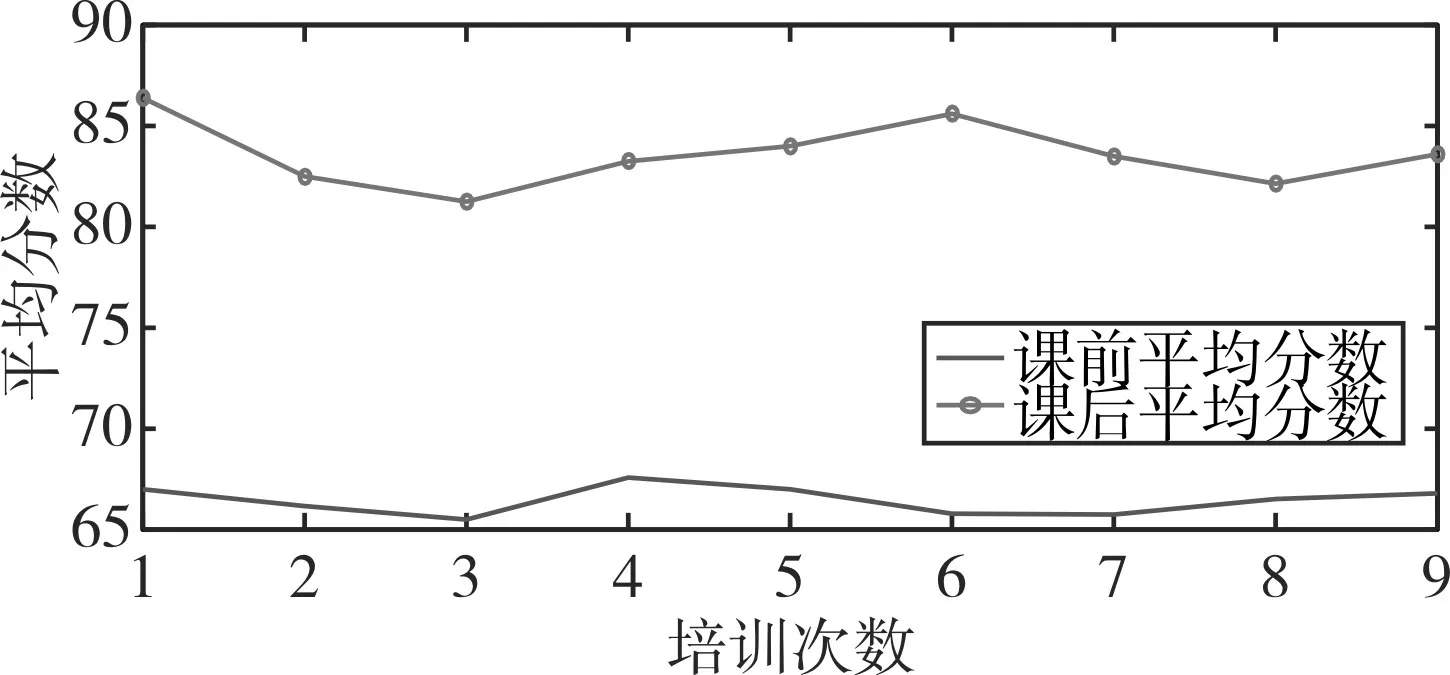
图7 学员的课前及课后成绩对比
利用灰度预测数学模型GM(1,1),将培训情况表达成基本规律,对课程及实例的安排是否符合国情进行预测。
具体步骤如下:
设有原始数据列:
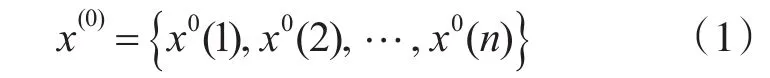
其中,X(n)为培训学员的课后测试平均成绩;n为培训次数。
将原始数据累加以便弱化随机序列的波动性和随机性,得到新数据序列:

式(4)中,a,u待定系数,分别称为发展系数和灰色作用量,a的有效区间是(-2,2),并及a,u构成的矩阵为灰参数a^。

5 基于灰度预测理论的培训效果中长期预测
5.1 数据序列的初始检验
灰色预测理论要求数据具有指数平滑性。对学员课前及课后测试成绩的原始数据进行光滑性检验,同时对一次累加生成序列X(1)进行指数规律的检验。
对原序列X(0)进行r次累加生成序列。当r充分大时,所得序列可以充分光滑,且光滑比趋于0。设原序列的光滑比为ρ(k):

原序列X(0)为准光滑序列,则需满足以下条件:
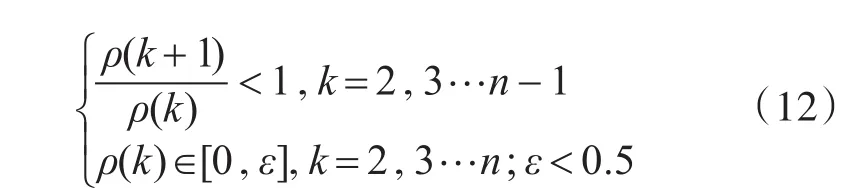
由式(12)可知,对于学员课前及课后成绩的原序列的光滑比序列分别为ρB(k)ρA(k),因此对应的原序列 XB(0)XA(0)为准光滑序列。
对序列X(0)的1-AGO序列进行准指数规律检验。一般情况下非负的光滑序列经过累加生成之后,随着其随机性的减少,呈现出近似的指数增长规律,且原序列越光滑。累加生成序列的指数性越明显。设原序列的级比为σ(k):

当k=2,3,…n时,原序列的累加生成序列具有准指数规律。经计算δ=0.474。上述分析表明,原序列 X(0)为准光滑序列。一次累加生成 X(1)序列具有准指数规律。能够对上述时间序列建立灰色预测模型。
5.2 数据数列预测结果分析
对学员培训成绩数列构建灰度预测模型,本研究利用Matlab对模型进行分析,预测未来第10、11批次学员的培训成绩,并将分析结果进行可视化,如图8及图9所示。

图8 课前测试历史分数与灰色模型预测分数

图9 课后测试历史分数与灰色模型预测分数
通过图8~9可以直观得到,第1期至第9期,学员平均分数与灰度模型的预测值接近,这也验证了模型对学员培训成绩运动较高的拟合程度。灰色预测模型在培训分数历史数据基础上预测了第10及11期学员课前测试平均分66、67分;课后测试平均分83、83.5分。
5.3 灰色预测模型性能检测
从发展系数范围检测、残差检验、后验差检验和关联度检验进行灰色预测模型性能检测。
1)发展系数范围检测
从灰色理论经验分析可知,随着发展系数仅取值的不同,对应的GM(1,1)模型适用范围存在显著的差异,一般而言,发展系数增加则模型的拟合误差随之增大。通过分析可知,建立灰色预测模型的发展系数为课前测试为0.04,课后测试为0.057,因此模型适宜于中长期预测。
2)残差检验
残差检验即对模型模拟值与实际值之间的残差进行检验。一般地,认为平均相对误差越小越好。通过分析可知,课前测试残差检验:0.0067,课后测试残差:0.0085,精度为一级。
3)后验差检验
后验差检验即对残差分布统计特征进行检验。均方差比值越小说明模型的拟合方差小,一般认为均方差比值越小越好。经分析可知,课前测试方差比C检验:0.9433,小误差概率P检验:0.5000;课后测试方差比C检验:0.7222,小误差概率P检验:0.7000。说明拟合效果较好。
6 结语
本研究以NDLS灾难医学培训为研究对象,对所采集的数据进行分析可知,目前的培训效果良好。学员分数的灰色模型预测值能够反映其历史培训效果的整体运行趋势及特征,是及时调整教学案例及方法的依据。所建立的灰色预测模型发展系数为0.04,模型适宜用于中长期预测。对模型的性能分析可知,拟合值分布均匀,因此所建立的灰色预测模型精度较高。通过对建立的灰色预测模型性能进行的检测结果,综合考虑发展系数范围检测、残差检验、后验差检验及关联度检验的结果,模型的预测精度较好,同时也验证了目前培训课程体系的可行性及有效性。
研究结果也可以作为国内同类培训的教学体系构建参考,同时可作为后续NDLS培训向民众推广灾难知识普及并制定相关指南的研究依据。
