萤火虫算法优化的卷积网络在图像显著性检测中的应用*

孙永盛 刘 镇

（江苏科技大学计算机学院 镇江 212000）

1 引言

随着计算机计算能力的提升与人工智能的发展，利用计算机模拟人眼的视觉注意机制，已成为计算机视觉领域重要的研究方向之一。图像的显著性检测是指通过建立图像显著性检测模型，准确快速地检测出图像中的人眼注视区域。完整的图像显著性检测模型需要充分模拟视觉注意机制，然而在实际运用中，由于计算方法和建模方法的限制，检测出的图像显著性区域与实际的人眼注视区域具有一定的差距，检测的准确度有待进一步提高，模型的检测速度经常受到严重的影响。

卷积神经网络是机器学习中广泛应用于图像处理领域的一种算法，但标准神经网络预测响应时存在的泛化能力差、收敛慢、网络预测精度不高等缺陷［1］。据此，本文基于混沌策略优化的萤火虫算法予以改进，优化神经网络初始权值和阈值以提高网络预测性能和精度。结合图像显著性检测的具体应用建立相应的检测模型，该模型在检测准确度和检测速度方面均有显著的提高，能够准确快速地检测出图像的显著性区域，并且具有广泛的适用性。

2 卷积网络的图像显著性检测

卷积神经网络模型是机器学习中应用于图像处理领域中的一种经典模型。它由特征提取层与特征映射层组成。网络层由卷积层和下采样层交替形成。卷积层和下采样层之后，是全连接层输出［2］。卷积神经网络结构图如图1所示，若输入图像大小为n×n，经过卷积层m个s×s的卷积核后，输出m 个(n-s+1)×(n-s+1)大 小 的 图 像，经 过 下采样层后输出m个(n-s+1)/2×(n-s+1)/2的图像，依次再经过卷积层和下采样层。

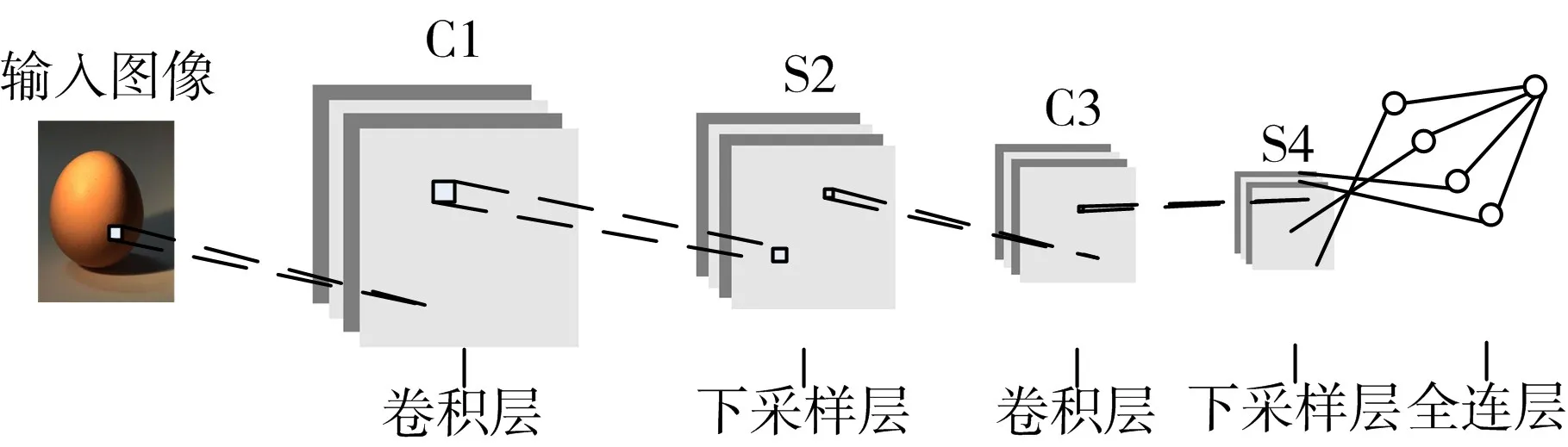
图1 卷积神经网络结构图

图1中C代表卷积层，S代表下采样层。卷积层用来进行特征提取，提高模型的鲁棒性，公式如下：

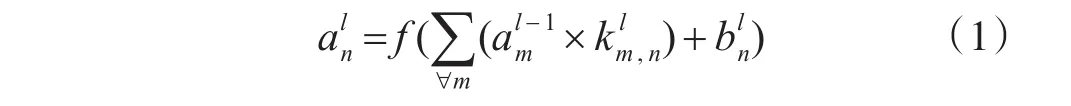
其中表示当前层所卷积出来的特征图；同样地，则表示前一层传递过来的下采样层的特征图；表示从上一层第m个特征图到当前层第n个特征图的卷积核；f(x)=1/[1+exp(-x)]为激活函数。代表神经元偏置，是卷积核与上一层特征图谱卷积和的响应，采用不同的卷积和则可以提取不同的特征［3］。下采样层是对特征进行映射，减少了特征的分辨率，节省了计算时间，增加量了模型的效率，下采样层中的节点输出可以表示为

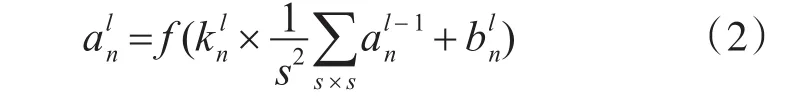
其中表示下采样层中采样模板的权值，s×s表示采样模板的尺寸。最后网络形成一个全连接层输出的最后结果，输出公式如下：

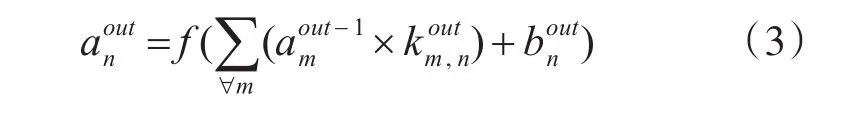
3 标准萤火虫算法

萤火虫优化算法（Firefly Algorithm）是一种新型仿生智能优化算法，该算法的仿生原理为：萤火虫个体总是朝最近、最亮的个体移动，未找到最近最亮个体的萤火虫规定其在原位置基础上进行无指导方向的运动；萤火虫之间的相对吸引力决定了个体的移动距离，越亮的个体其对周围萤火虫的吸引力越大，同时对越远萤火虫的吸引力越小［4］。

对于待优化问题，其对应的优化函数在定义域中的取值可以作为判断萤火虫亮度高低的标准，萤火虫的位置对应优化函数在定义域中的解。亮度越高的萤火虫所对应的目标函数值越优，随着种群不断进化，整个种群不断接近最亮的个体，最终获得优化函数的最优解即对应最亮个体位置［5］。

在萤火虫优化算法中，个体i到j的距离表示为rij，一般采用欧氏距离［6］，即：

其中d代表搜索空间的维度。

由定义萤火虫个体i对j的吸引力和其对j的相对亮度成正比，可得萤火虫i对萤火虫j的吸引力公式表示为

式中，β0表示萤火虫在光源处的吸引力，在光源位置rij=0，此时萤火虫具有的吸引力最大，通常取β0=1，γ为光吸收系数，该参数的取值影响萤火虫优化算法的搜索速度和最终寻优质量［7］。

萤火虫i相对萤火虫j的荧光亮度公式为

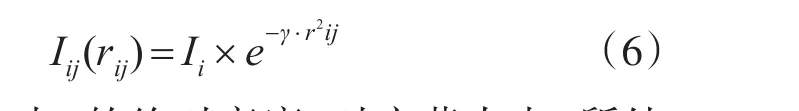
式中，Ii是萤火虫i的绝对亮度，对应萤火虫i所处位置的目标函数值：γ表示光吸收系数，从光学角度描述了亮度在传播过程中会被介质吸收，同时由于距离增加而不断变暗，一般情况下对γ取常亮［8］。

萤火虫j被萤火虫i吸引，j向i移动来更新原来位置，j位置更新公式为

式中，t为算法的迭代次数，xj(t+1)代表萤火虫j在第t+1次迭代的位置；βij表示个体i对j的吸引力：α为常数，取α∈[0，1]；rand代表随机数，在[0，1]上服从均匀分布。

4 基于混沌化策略的种群初始化

混沌现象是一种普遍存在于自然界中的一种复杂随机现象，它具有随机、遍历、规律、敏感等特性。从表面上看，混沌运动与随机运动很相似，但是两者存在本质的区别。混沌运动是由于确定性的物理规律所形成的，是可以短期预测的［9］。而随机特性是由内在特性的外部噪声所产生的。混沌优化就是通过随机、遍历和初始值敏感等这些混沌运动所具有的特点来对随机算法的性能进行改进。

在多种混沌序列的模型中，可知在混沌空间相同的条件下，由逻辑自映射函数生成的序列比logistics映射更具有遍历性［10］。采用逻辑自映射函数生成混沌序列，如式（8）所示：

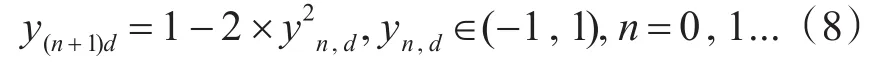
其中，为避免混沌序列出现全为1或0.5的情况，所以初始值不能取0和0.5，d表示D维搜索空间的第d维。

初始化混沌种群的过程［11］描述如下：

1）对于D维空间的M个萤火虫个体，根据逻辑自映射函数的性质，首先初始化混沌变量，在(-1，1)区间随机产生初始变量。

2）按照式（8）迭代，将逻辑自映射生成的MaxGen×D-1个混沌变量，与初始混沌变量一起对应全部MaxGen×D个萤火虫个体。

3）讲产生的混沌变量序列按变换到目标函数的搜索空间，生成萤火虫初始种群的M个个体，公式如下：

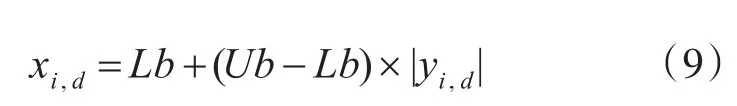
式中，Lb和Ub分别表示搜索空间第d维的下限和上限，yn，d是根据式（9）产生的第i个萤火虫对应的第d维混沌变量，xi，d为第i个萤火虫在搜索空间中第d维的坐标值。

传统萤火虫算法和基于混沌优化策略的种群初始化效果分别如图2所示。

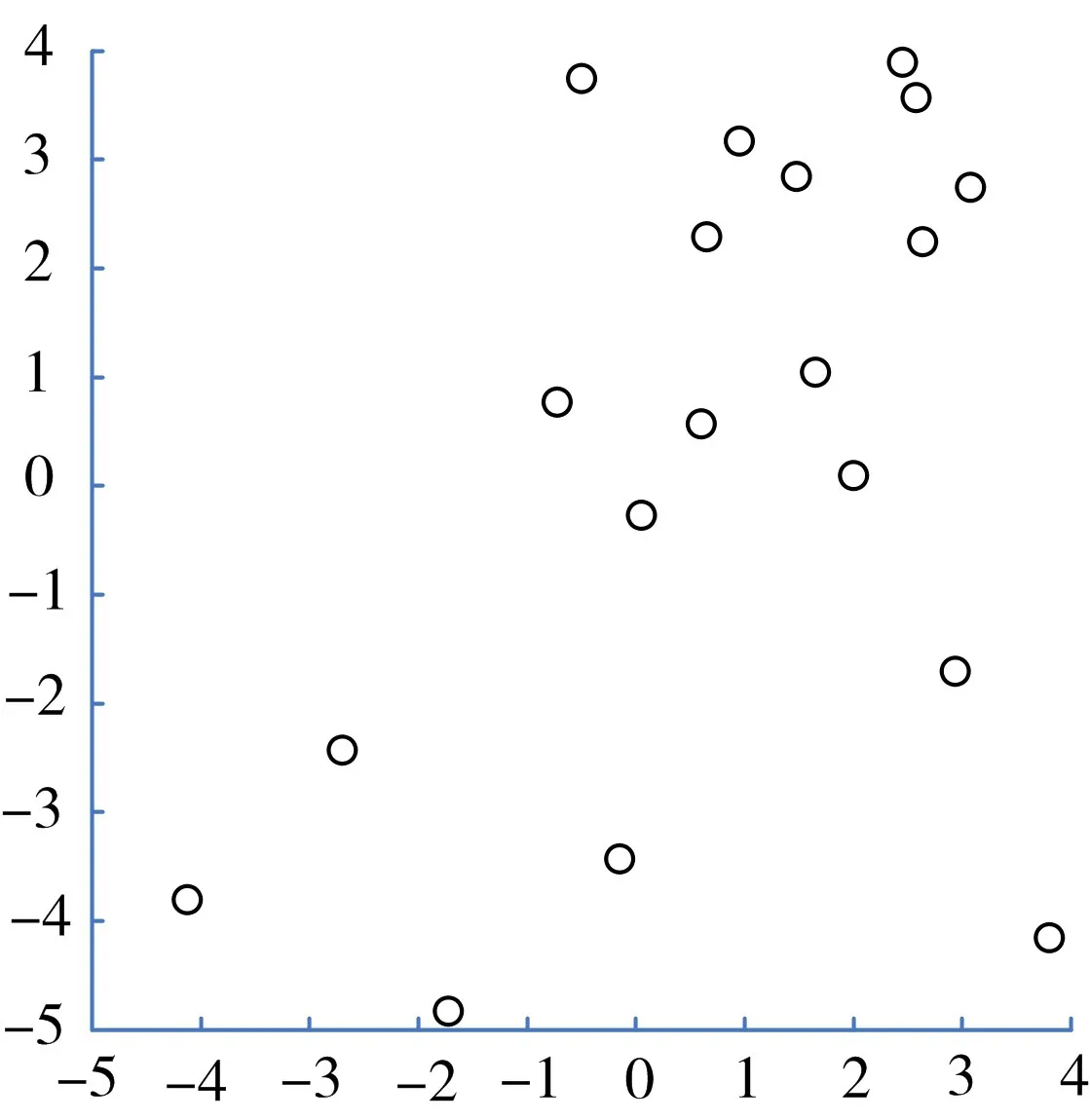
图2 传统萤火虫算法的种群初始化效果图

从图2和图3的初始化种群分布对比可以看出，采用混沌优化策略的初始化种群，种群分布的均匀性要明显优于采用随机策略的初始化种群。

图3 基于混沌优化策略的和群初始化效果图

5 基于萤火虫算法优化的神经网络

神经网络结构通常包含输入层、隐含层和输出层。输入、输出层节点数由训练样本的输入、输出维数确定［12］。隐含层的节点数根据经验公式选定。

各层之间的传递函数为Sigmiod函数，隐含层第j个节点的输出：

式中wij为输入层第i个节点到隐含层第j个节点的连接权值；θj为隐含层第j个节点的阈值；pi为隐含层第i个输入。将隐含层输出hj进一步向后传递，相应得到输出层第k个节点的输出［13］：

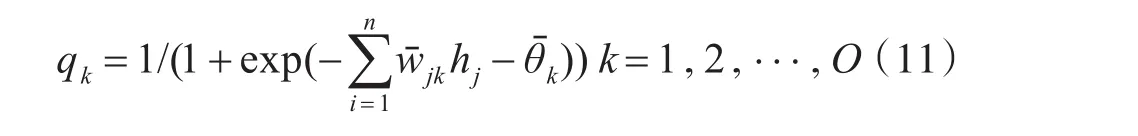
式中：wˉjk为隐含层第j个节点和输出层第k个节点之间的连接权值；θˉ为输出层第k个节点的阈值［14］。

萤火虫神经网络训练时，每个萤火虫个体xi代表神经网络各层的连接权值wij、wˉjk和阈值θj、θˉk，个体编码采用实数矢量形式［15］，则编码长度（即需要优化的变量总数）由各层节点数N，H和O决定。

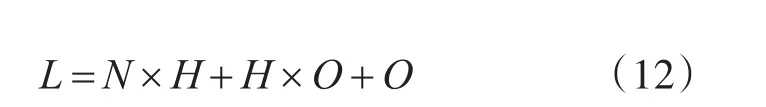
训练时，神经网络的训练精度由误差RMSE来衡量：

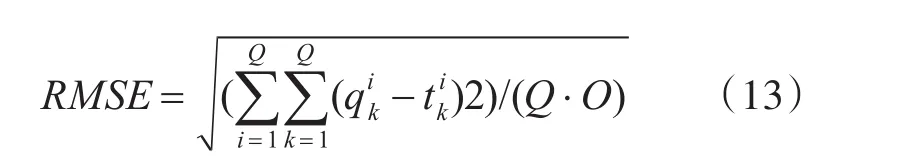
式中：Q为训练样本数；为第i个训练样本在输出层第k个节点的期望输出。

萤火虫神经网络训练过程中，萤火虫每一个个体代表一个神经网络，神经网络的性能用训练误差来表示，萤火虫个体的适应度值可以直接取为该个体代表的网络训练迭代终止时的误差值［16］。

算法流程如图4所示。

图4 算法流程图

6 实验分析

6.1 实验条件及评价指标

本文在MSAR图像数据库上进行实验。该图像数据库包含动物、植物、人等多种图像，是显著性检测的常用数据库［17］。本文中的实验环境为Matlab r2014b，CNN网络采用五层经典结构。

为了体现显著性检测效果，本文采用F-Measure来评价它能够同时考虑到检测的准确率和完全率［18］。计算公式如下：

其中，P代表示检测的准确率；R表示检测的完全率；α用来衡量F-Measure值是侧重于检测的准确率还是完全率，本文取α为0.3，表示侧重于检测的准确率［19］。

6.2 结果分析

将MSAR图像数据库中的图片分别在AC、FT、SF、SR四种经典的显著性检测算法［20］上运行，并与本文算法运行结果、标准GT集对比，结果如图5所示。

由图6的实验数据结果可以看出本文算法的P，R，F-Measure值均高于其它四种算法，证明本文提出的显著性检测算法有一定的合理性和优势。

图5 对比结果

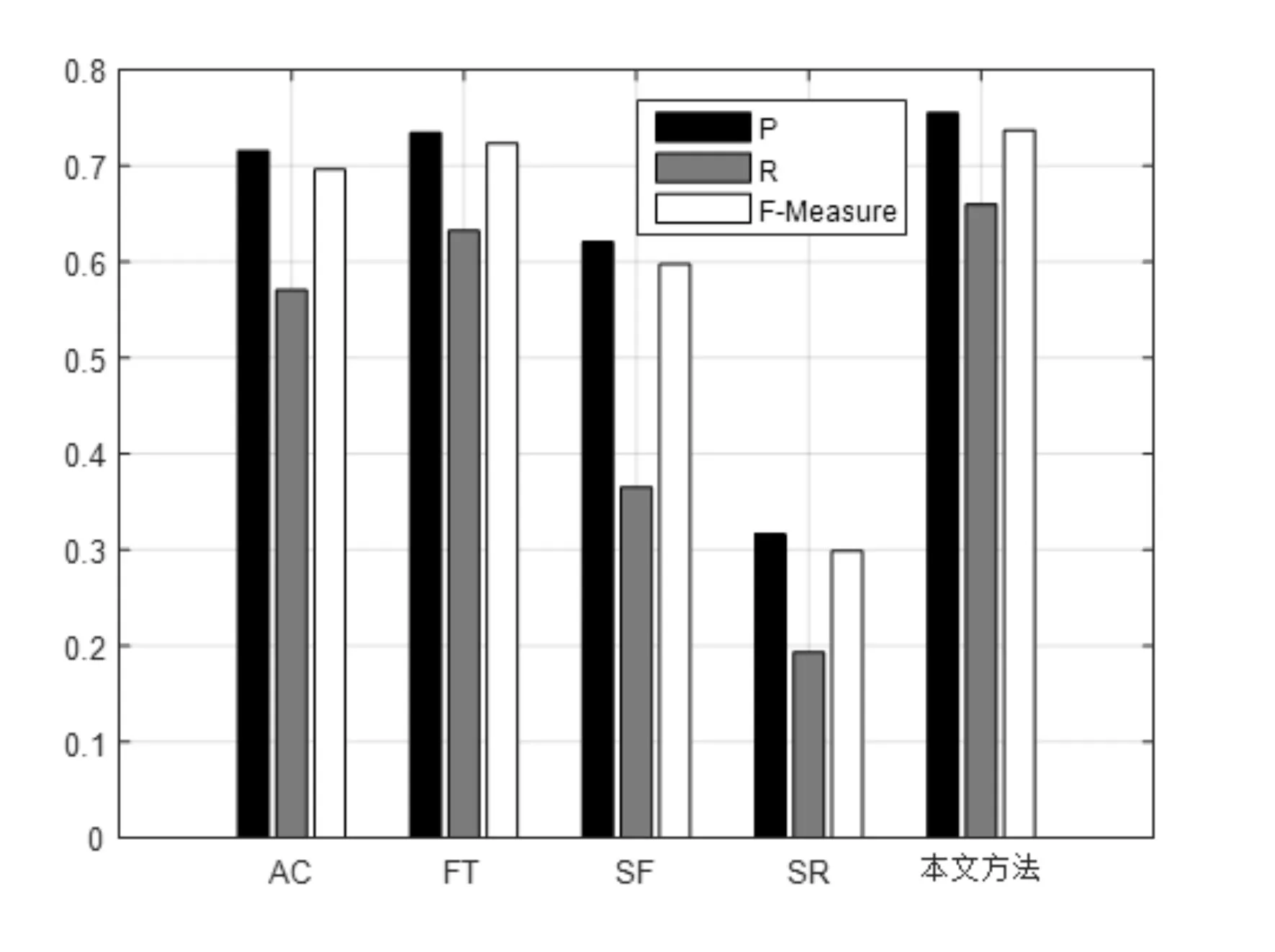
图6 实验数据结果

7 结语

本文将混沌序列用于萤火虫算法的种群初始化，提高了萤火虫算法初始种群分布的均匀性。构建了萤火虫算法优化的神经网络预测模型，优化了神经网络初始权值和阈值，提高了预测性能和精度。该模型不依赖于目标的形状、环境和场景的变化，具有较好的鲁棒性。利用卷积神经网络有效地提取显著性特征，经过特征融合进行显著性检测。结果显示，在主观观测和客观计算结果上显著性效果均有一定的提高，显著性结果图片在清晰度和准确度上也有一定的提高。但对比方法和本文方法都停留在单目标无法很好地处理多目标显著性的检测，后续将对多目标的显著性检测进行研究。