改进的k-means算法在三支决策中的应用研究*
2020-08-11蔺艳艳陆介平王郁鑫傅廷妍
蔺艳艳 陆介平 王郁鑫 傅廷妍
(江苏科技大学计算机学院 镇江 212001)
1 引言
随着互联网在生产生活中应用的越来越广泛,随之产生的是大量的数据。这些数据往往潜藏着用户的行为动向或某个行业的发展规律。如何从这些海量数据中挖掘到有价值的信息是我们今天的研究热点。聚类是数据挖掘中的一个非常重要的分支,它是根据信息相似度原则在预先不知道预划分类的情况下进行信息聚类的一种方法。k-means算法[1]是一种典型的基于划分的聚类算法,自1967年MacQueen提出后,由于其具有算法简单易懂且收敛速度快的优点,得到较普遍的应用[2]。比如,利用k-means聚类方法来对客户进行准确的分类,其结果可以作为企业优化营销资源的重要依据等等。
但是,传统的k-means算法是二支聚类,它不适用具有不确定因素的环境,并且k-means算法需要预先随机选取初始聚类中心和设定聚类数目[3],这些因素将导致聚类结果不稳定,影响其精确性。有许多学者对k-means算法进行研究和改进,Feng等改进k-means算法[4]是根据数据点的距离构造最小生成树,并加以剪枝来构造样本分布情况,从而动态选取初始聚类中心。Yu等提出了一种结合关系矩阵和度中心性(Degree Centrality)的分析方法,从而确定k-means算法初始的k个中心点[5]。为了能自动选择k-means算法的初始k值,Debatty等提出了 G-means算法[6],Yuan 等加入密度参数并通过计算平均密度来降噪[7],Kettani等提出AK-means算法[8]等。但是,这些方法对局部最优、聚类结果不稳定和总迭代次数多等问题进行优化,并且在处理不确定性信息时,考虑到当前获取到的信息不够充分的特点,如果强制将其中的元素划分到一个类中,往往容易带来较高的错误率或决策风险。基于此,Hoppner等提出用模糊集表示聚类结果的模糊聚类理论方法[9],Lingras提出了粗糙聚类方法,将聚类结果由粗糙集的正域,边界域和负域来表示[10-13],Yao等用区间集来表示聚类结果中的一个类[14]等,这些方法计算复杂,对指标权重矢量的确定主观性较强。三支决策聚类理论的提出,有效地改善了传统聚类方法处理具有不确定性因素的问题,并且可与传统聚类算法结合,计算相对简单。
三支决策聚类是一种重叠聚类,早先由Yao、Yu[15~17]等提出,它采用核心域、边界域和琐碎域来表示每个类别,其中边界域中的元素是介于核心域和琐碎域之间的元素,集中对边界域中的元素判断处理,可以较好地处理具有不确定性对象的聚类问题。在三支决策理论中,传统的k-means二支聚类算法是一种特殊的三支聚类,即边界域中的元素为空。有学者Li[18]利用传统k-means聚类算法产生的结果和每个类中元素的邻域所在的集合进行收缩与扩张,来研究将二支聚类转化为三支聚类的方法,达到提高聚类结果的数据结构的目的。但是,这些方法均是直接使用传统k-means算法,聚类结果的准确性和确定性受k-means算法缺点影响。
针对传统k-means算法不适用具有不确定因素的环境和现有的基于k-means的三支聚类分析中并未避免传统k-means聚类随机选择初始簇中心而导致聚类结果不稳定的问题,本文提出一种改进的k-means聚类方法,避免了传统k-means算法由于初始簇中心选择的随机性而导致聚类结果不稳定的现象;其次,为了避免传统k-means算法在处理不确定性信息时,强制将其中的元素划分到一个类中带来的错误率或决策风险,将改进的k-means算法与Wang提出的将二支聚类结果转换成三支聚类方法结合起来,研究本文所提出的方法在三支决策中的应用,以提高聚类结果的结构和精度,实验结果证明这种方法是有效的。
2 相关知识
2.1 k-means算法
k-means算法[19]原理简单易懂,时间复杂度低,仅为O( )kNT ,并且具有计算简单、高效等特点,广泛应用在生产生活的各个领域。k-means算法基于样本间相似度原则,采用两样本间的欧氏距离远近作为衡量标准进行数据集划分。k-means的算法理论是:在数据集D中,先随机选取k个样本作为初始中心,再计算剩下的所有样本到这一组初始中心的欧氏距离,根据距离最近原则将各个样本归入到相应的聚类中心所在的类,然后计算每个类的新均值,重新修正聚类中心。不断迭代更新,直到误差平方和函数稳定在最小值。

其中:k为聚类类别数,ri为第i类中的样本的个数,ni为第i类中样本的平均值。
2.2 三支决策聚类的相关概念


其中式(3)表明,可通过和来表示一个类,式(4)要求正域非空,即每个类中至少有一个对象,而式(5)保证每个对象至少被分到一个类中。与二支聚类结果不同,三支聚类的结果可由下式来表示:

2.3 基于传统k-means算法的三支聚类
二支决策的聚类结果是对象一定属于两个类中的一个,而三支决策的聚类结果是:对象确定属于某类、可能属于某类或确定不属于某类。可以说二支决策是三支决策类结果中的一种,即不存在边界区域。


图1 数据集图
如果删除x1和x2,则很容易地将图1聚成两个结构特征非常好的类,而无论将x1或x2放到哪一个类中均会降低这个类的紧致性。基于三支决策聚类的核心思想,将x1和x2放到两个类的边界域当中去。定义一个θ域(距离该点最近的θ个点组成的集合),使θ域内的点在二支聚类的结果下不完全包含于某个类中,例如x1和x2这类点。这样先采用k-means聚类的结果,再结合θ域(边界域)的进行决策聚类的方法,便是基于传统k-means算法的三支聚类。
3 改进的k-means算法在三支决策中的应用研究
3.1 改进的k-means算法
传统的k-means算法的缺点是随机地选取任意k个样本作为初始聚类中心,这种随机性会影响最终聚类结果的稳定性。本文提出的k-means算法的改进能够克服上述问题。首先,先对数据集进行凝聚层次聚类,并采用轮廓系数对不同层次划分进行评估,获得较为合理中心数K。再对数据集进行n次样本抽取(n次抽取的样本总数要大于等于原始样本数),并以层次聚类所得K值做为输入对其进行k-means聚类,从而得出一组中心。然后计算这n组中心的误差平方和准则函数值,选择值最小所对应的聚类中心作为初始聚类中心。最后将其作为k-means三支聚类算法的初始中心和k值的输入,避免了k-means算法随机选择初始中心和k值而导致最终三支聚类结果不稳定的问题。其中,多次抽取样本可以保持随机性不被破坏。层次聚类算法可以在其聚类结果上采用轮廓系数对数据集的不同层次划分进行评估,在初始中心确定前先初步优化簇数K,最终的初始中心是由收敛函数来选取。为防止因适应误差平方和准则函数而陷于局部最优或导致簇过度划分,可以采取设定初始聚类中心数大于指定的K值,并且设定准则函数收敛标准,使达到收敛后的初始聚类中心数在合并距离近的簇之后数量减少到指定的K值。
层次聚类中需要用的公式具体如下:

3.2 改进的k-means算法在三支决策中的应用研究
本文将层次聚类和科学抽样法引入到k-means算法中,是为了获取最优初始簇类的数目,避免k-means算法随机选择k值和初始聚类中心而导致分类结果误差较大、聚类结果不稳定等问题。然后将改进后的k-means算法聚类的结果做为三支聚类的初始输入,实现最优类别划分的问题。
前文提到的θ域这里给出详细定义:

因为θ的选取也会对最终聚类结果产生影响,所以选择合适的θ很重要,这里选取的θ是数据集中样本数目的开平方,即N。
算法1:改进的k-means算法在三支决策中的应用

Step1:通过式(6)、式(7)将U中所有样本都合并成一类,利用轮廓系数对聚类结果进行评估,得到较为合理的K值;
Step2:对U进行多次抽样,通过式(1)对每次抽取的样本进行k-means聚类,得到一组中心;


4 几种聚类性能度量的指标
4.1 平均轮廓系数
轮廓系数(silhouette coefficient)[20]是聚类效果好坏的一种评价方式,它结合内聚度和分离度两种因素,在相同原始数据的基础上,评价不同算法或算法的不同运行方式对聚类结果所产生的影响。
计算某一个点的轮廓系数公式:
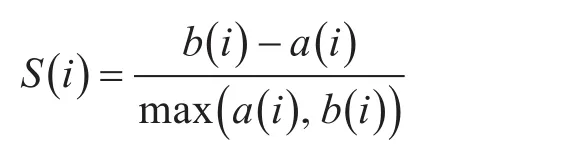
其中:表示i点向量到与它同簇的其他点的平均距离;表示i点向量到与它异簇的点的平均距离最小值。由上式可知,轮廓系数的值为[- 1,1],如果轮廓系数S(i)值越大,则表明i点所在的簇就越紧密。
对于整个数据集来说,其轮廓系数的计算公式如下:

其中:n表示数据集中的样本总数;SC值越大,则聚类效果越好,反之越差。
4.2 Davies-Bouldin-Index评价准则
Davies-Bouldin-Index(DBI)[21],聚 类 结 果 的DBI越小,聚类效果越好。公式如下:
4.3 准确率
准确率(accuracy)是常见的一种评价聚类性能的外部指标。准确率越高,聚类效果越好。计算公式为

其中N是所有已被确定类别的对象的总数,k是聚类数,θi是第i个类中正确划分的数据对象的个数。
5 实验结果与分析
本节选用5组标准UCI[22]数据集对本文提出的算法进行测试实验来验证方法的性能。表1列出了实验中所使用的5组测试数据集的基本信息。对于每个数据集,重复进行了200次实验,用200次的平均值作为算法性能差异比较的依据。

表1 实验所使用的数据集
本文设置两个实验来说明提出的改进的k-means算法以及基于改进k-means算法的三支决策的聚类效果和准确率。将改进的k-means算法记为k-means PA。
第一个实验是二支聚类的测试,通过对比一些已有的算法,即首先用fuzzy c-means、k-medoid、传统k-means和k-means PA分别在表1中的数据集上进行聚类来验证本文提出的k-means PA算法的聚类结果DBI和准确率,以及聚类结果的稳定性。
第二个实验是在第一个实验的基础上,结合本文介绍的三支决策方法进一步优化聚类结果。最后通过实验数据分别比较二支聚类和三支聚类两组实验结果的DBI和ACC。
5.1 实验一
图2是fuzzy c-means、k-medoid、传统k-means和k-means PA四种算法表1中的数据集上进行二支聚类后结果的DBI对比图。由图可知,本文提出的算法k-means PA在UCI的5个数据集上,其DBI均低于fuzzy c-means、k-medoid和传统k-means的DBI,在Sonar数据集上尤其明显。在Wine数据集上,本文算法与传统k-means基本相同,低于fuzzy c-means和k-medoid。
图3是fuzzy c-means、k-medoid、传统k-means和k-means PA四种算法表1中的数据集上进行二支聚类后结果的准确率对比图。由图可知,本文提出的算法k-means PA在Iris数据集上的准确率没有 fuzzy c-means、k-medoid的 ACC 高,但比传统k-means的准确率要高;在Hill、Sonar和Wine数据集上,k-means PA的准确率要高于其他三种算法;在Wdbc数据集上,k-means PA的准确率和其他三种算法的准确率不分伯仲。

图2 算法DBI实验结果

图3 算法准确率实验结果
综合图2和图3来,本文提出的改进算法在UCI的5个数据集上获得了较好的DBI和准确率,因此,本文的算法能适应于不同数据集的聚类挖掘。
5.2 实验二
实验二是在实验一的基础上进行的三支聚类,图 4和图 5是基于 fuzzy c-means、k-medoid、传统k-means和改进k-means算法结合三支聚类理论的聚类结果的DBI和ACC对比图。

图4 三支聚类结果DBI对比图
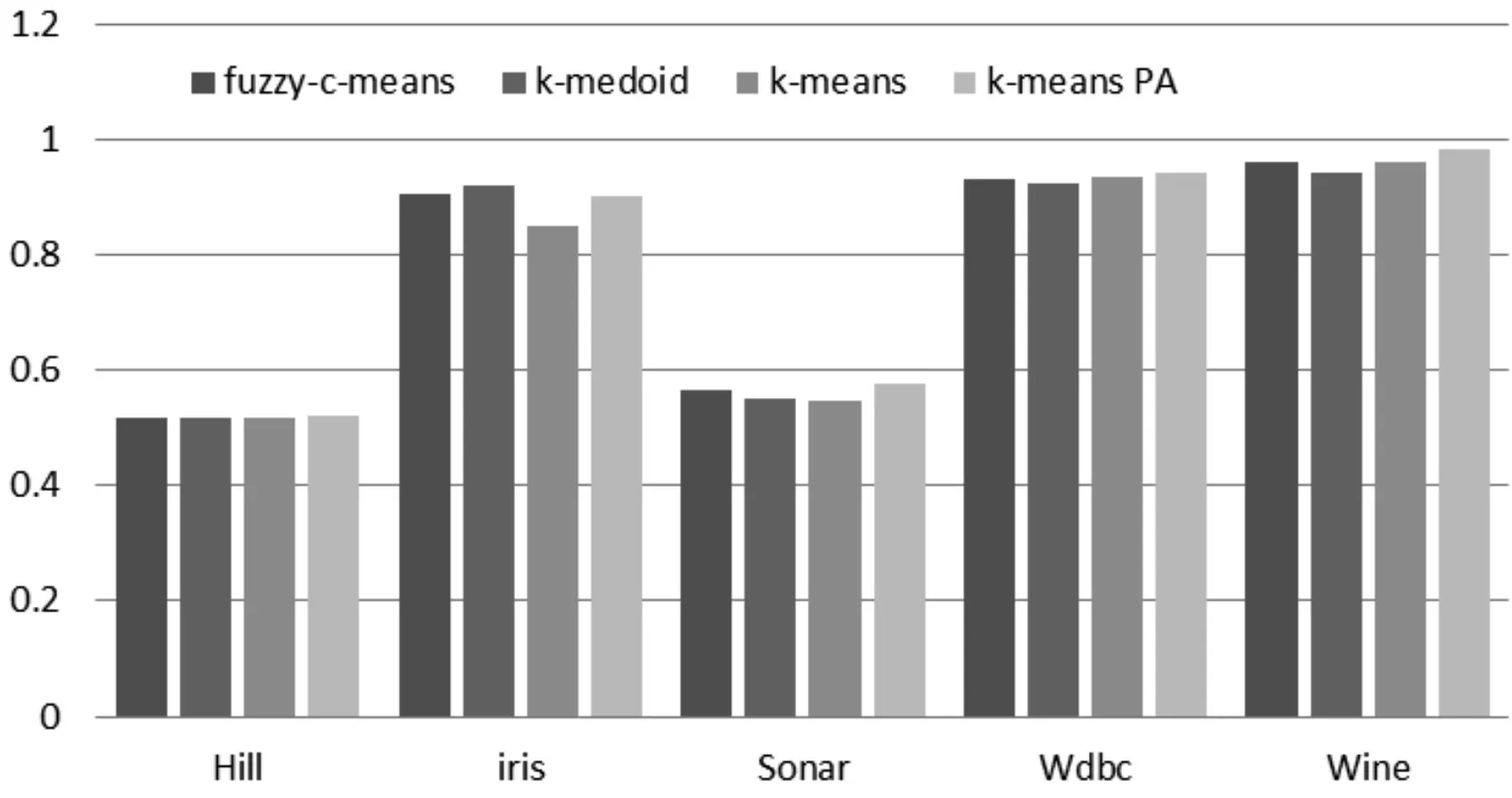
图5 三支聚类结果ACC对比图

图6 基于k-means PA的二支聚类和三支聚类结果的DBI和ACC对比图
由图可知,三支聚类结果的DBI和ACC对比结论同实验一。但从图6中可以明显看出基于本文提出的k-means PA算法的三支聚类结果的DBI比k-means PA二支聚类结果的DBI低,基于本文提出的k-means PA算法的三支聚类结果的ACC比k-means PA二支聚类结果的ACC高,这表明结合三支聚类方法的聚类效果更好,准确率更高。综上所述,本文提出的改进的k-means算法在三支聚类算法中应用是有效的。
5.3 稳定性
由于传统k-means算法在聚类时结果存在不稳定现象,因此,对提出改进行算法的聚类结果进行了稳定性实验。选取其中一个数据集并进行30次运行实验,其结果如图7所示。从图7可以看出,传统的k-means算法稳定性较差,结果会随着运行次数不同而呈现不同的聚类结果,而本文提出的聚类算法的聚类结果呈现出较好的稳定性。

图7 算法稳定性比较
6 结语
本文针对传统k-means聚类算法初始中心的选取做了改进,并结合Yu等学者研究的基于邻域的三支聚类理论,提出一种改进的k-means算法并结合三支聚类的算法,解决了初始中心和k值的选取问题和处理不确定性信息时最优类别划分的问题。实验结果证明,本文所提出的算法可以有效地避免传统k-means因随机选取初始簇而导致了聚类不稳定的现象,并且算法在准确率上有所提高,DBI表明聚类的效果更好。但计算的时间有所增加,如何快速有效地获取一个最优参数k来使聚类效果和精度能达到一个最佳理想的结果,还有研究近邻参数θ的值将会是下一步的研究工作内容。
