一种高超声速飞行器再入轨迹优化方法
2020-08-11王宏伦
余 跃,王宏伦
(1. 北京航空航天大学自动化科学与电气工程学院, 北京 100191; 2. 北京航天自动控制研究所, 北京 100854; 3. 北京航空航天大学飞行器控制一体化技术重点实验室 , 北京 100191)
0 引 言
高超声速飞行器因具有飞行速度快、突防能力高、生存能力强、全球精确打击和毁伤威力大等独特优势,已成为当今世界各国争相研制的武器[1]。再入轨迹优化是高超声速飞行器研究中的主要关键技术,是指根据飞行任务的飞行条件和技术指标,基于飞行器动力学模型求解控制量与运动状态的最优时间序列,从而寻找一条某种性能指标最优而又满足各种约束的飞行轨迹[2-3]。再入环境的复杂性和不确定性以及再入过程中受热流密度、动压、过载的严格约束,再加上对终端状态的严格要求,给再入轨迹优化技术的研究提出了挑战[4]。
按照是否直接对性能指标进行寻优,可将轨迹优化方法分为间接法和直接法。间接法是基于经典的变分法或者Pontryagin极小值原理,将最优控制问题转化为哈密尔顿两点边值问题进行求解。与间接法不同,直接法是将最优控制问题中的变量离散并参数化,从而将最优控制问题转化为非线性规划(NLP)问题,再结合数值优化方法进行求解。直接法中的伪谱法采用全局正交多项式逼近状态变量和控制变量,具有精度高且收敛性好的优点,近年来迅速成为飞行器轨迹优化领域应用最广泛的研究方法[5]。
雍恩米等[6]针对再入轨迹优化问题,提出了基于高斯伪谱法(GPM)的串行分段优化策略,具有较高的精度和计算效率。宗群等[7]针对临近空间飞行器上升段的轨迹优化问题,提出了将GPM和序列二次规划相结合的求解策略。明超等[8]针对超声速导弹爬升段的轨迹优化设计问题,利用hp自适应伪谱法构造了一种较为通用的优化求解策略。张志国等[9]将GPM运用在液体运载火箭抛罩结束到入轨飞行段的制导律设计中。尽管伪谱法具有精度高、收敛快和应用灵活的优点,但仍存在以下缺陷:1)需要目标函数的梯度值;2)相对差的全局搜索能力;3)需要合适的初始猜测值[10-11]。当面对复杂的轨迹优化问题时,对初始猜测值的敏感可能会导致没法得到全局最优解。
近年来,各种启发式优化算法不断被提出,如粒子群算法(PSO)[12]、鲸鱼算法(WOA)[13]、灰狼算法(GWO)[14]等,这些算法不依赖目标函数的梯度信息、对初始猜测值不敏感和具备强大的全局搜索能力,被广泛应用于各类优化问题。樽海鞘群算法(SSA)[15]是最新提出的一种启发式算法,通过模仿樽海鞘的捕食行为来求得全局最优解,从优化的统计数据看,SSA算法与当前顶级的启发式算法相比具有优势。
基于上述分析,为了充分利用启发式优化算法和伪谱法的优势,本文首先针对SSA算法中探索和利用的平衡过程加以改进,提出了一种新颖的动态自适应樽海鞘群算法(Dynamic Adaptation SSA, DASSA),将DASSA算法和GPM算法相结合,提出了一种新颖的DASSAGPM算法,并运用于高超声速飞行器再入轨迹优化问题中。DASSAGPM算法既能利用DASSA算法强大的全局搜索能力,又能利用GPM算法收敛速度快的优点,具有满意的优化性能。
1 再入轨迹优化问题
1.1 三自由度运动方程
不考虑地球自转的影响,建立高超声速飞行器三自由度无量纲运动方程如下[6]:
(1)
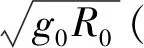
(2)
式中:K=0.5R0S/m;ρ为大气密度,CL和CD分别为升力系数和阻力系数,S为飞行器参考面积,m为飞行器质量。
1.2 约束条件
1.2.1过程约束
(3)
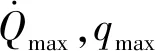
1.2.2控制边界
为使飞行器稳定飞行,控制量攻角α和倾侧角σ需满足如下条件:
(4)

1.2.3终端约束
为了满足与末制导段的交接班要求,再入终端状态需要满足终端约束条件,一般为地心距和经纬度组成的位置约束,某些飞行器对速度、航迹倾角和航迹偏角也有终端约束要求。用公式表示为:
(5)
式中:下标“f”表示终端状态。
1.3 目标函数
通常情况下,目标函数根据特定任务选定。对高超声速飞行器来说,可选为最小化热载、最大化航程、最大化横程或者最小化到达时间等。本文选择最小化热载为优化目标,同时考虑弹道平滑的因素,取综合性能指标为:
(6)
式中:c为加权系数,本文优化的主要指标为热载,故取c=0.8。
1.4 问题描述
基于上述分析,再入轨迹优化问题可描述为:在满足动力学方程(1)以及多种约束(3)~(5)的条件下,寻找最优控制量攻角α和倾侧角σ使得目标函数(6)最小。更为一般化的最优控制问题可描述为:寻找控制变量u(t),使得具有一般性的Bolza型性能指标最小
J=Φ(x(τ0),t0,x(τf),tf)+
(7)
且满足动力学微分方程约束
(8)
边界条件约束
φ(x(τ0),t0,x(τf),tf)=0
(9)
以及不等式约束
C(x(τ),u(τ),τ;t0,tf)≤0
(10)
2 樽海鞘群算法和高斯伪谱法
2.1 樽海鞘群算法
从海洋生物樽海鞘的航行和捕食行为中受到启发,Mirjalili提出了SSA算法,并用于解决优化问题。具体来说,将整个樽海鞘种群分为领导者和跟随者,领导者负责带领整个种群,跟随者彼此跟随。通过这种方式,整个种群逐步向食物位置(即全局最优点)移动。领导者的位置通过以下公式更新:
(11)
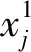
(12)
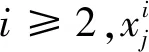
2.2 高斯伪谱法
首先简单介绍一下高斯伪谱法的基本原理。在一系列Gauss点上离散运动学方程中的状态变量和控制变量,并以这些离散点为节点构造Lagrange插值多项式来近似状态变量和控制变量。状态变量对时间的导数通过对全局插值多项式求导来近似,从而将微分方程约束转化为一组代数约束。终端状态可以由初始状态和高斯积分联合表示,目标函数中的积分部分也可以由高斯积分表示。通过变化,可将最优控制问题转化为具有一系列代数约束的NLP问题。
1)时域变换
采用GPM求解轨迹优化问题时,由于所涉及的正交多项式的正交区间是τ∈[-1,1],因此需要将时间区间[t0,tf]转换到[-1,1],可对时间变量t做如下变换:
(13)
2)状态和控制变量近似
GPM的配点τk(k=1,2,…,N)为N个LG(Legendre-Gauss)点,即N阶Legendre多项式的根。配点分布区间为(-1,1),加上边界点τ0=-1,作为区间[-1,1)的N+1个节点。因此,状态变量x(τ)可由N+1个Lagrange插值多项式的组合来近似:
(14)
类似地,控制变量u(τ)可由N个Lagrange插值多项式的组合来近似:
(15)
3)微分方程约束
对式(14)求微分,可得
(16)
式中:微分矩阵Dki可以离线确定
(17)
式中:PN(τ)为N阶Legendre多项式。从而将动力学微分方程约束转化为代数约束:
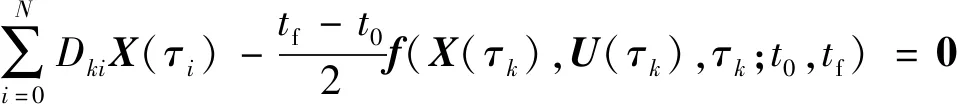
(k=1,2,…,N)
(18)
4)终端状态约束
由于式(14)中状态变量的近似忽略了终端时刻τf,因此需要补充终端状态约束:
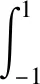
(19)
将终端约束条件离散并用Gauss积分来近似,可得:
U(τk),τk;t0,tf)
(20)
5)目标函数近似
将目标函数(7)中的积分项用Gauss积分近似,可得:
(21)
边界条件约束(9)和不等式约束(10)离散为:
φ(X(τ0),t0,X(τf),tf)=0
(22)
C(X(τk),U(τk),τk;t0,tf)≤0
(23)
经过上述变换,原最优控制问题转化为一个NLP问题。
3 基于DASSAGPM的再入轨迹优化
3.1 动态自适应樽海鞘群算法
本质上来说,智能优化算法都会面临陷入局部最优的问题,因此改进策略都是围绕着平衡算法寻优的探索和利用过程、避免陷入局部最优来展开。
从式(11)可以看出,系数c1(l)是平衡优化过程中探索和利用的主要参数。随着迭代次数的增加,c1(l)不断减小,可见优化前期重探索,更加注重全局搜索能力,后期重利用,更加注重局部搜索能力。虽然这一变化趋势是合理的,但是这种变化机制是被动的,没法根据当前种群优化状况进行动态精确的调整。为了使种群更加合理地进化,本节在传统SSA算法的基础上,借鉴经典控制理论中的“反馈”思想,引入种群改善率作为反馈量来动态自适应更新系数c1(l),提出了一种新颖的DASSA优化算法。
定义种群改善率R=Ms/M,其中Ms为当前种群中比上一代更接近全局最优解的个体数,M为种群大小。根据1/5原理,算法参数应该动态自适应变化以使种群改善率为20%[17]。所以,当R<0.2时,表明探索能力强而利用能力弱,此时应该减小c1(l)来提高搜索精度。当R>0.2时,种群主要在进行局部寻优,此时应该增大c1(l)来提高全局搜索能力。当R=0.2时,探索和利用达到了合理的平衡,此时不需要对c1(l)进行动态自适应调整。上述动态自适应规则可以表示为:
(24)
式中:c1(l-1)为上次迭代的调整系数,0<ζ<1为学习因子。
需要说明的是,式(24)中将不需要调整c1(l)的范围由R=0.2扩大至0.2≤R≤0.3,这是由于R=0.2出现的概率很低,会导致c1(l)频繁变化,不利于参数自调整的稳定。
3.2 基于罚函数法的约束条件的处理
SSA优化算法最初被提出是用来解决不带约束的静态优化问题,而再入轨迹优化问题包含多种约束,没法直接利用SSA算法求解,而是需要对约束进行处理。一般来说,罚函数法是最为普遍的约束处理方法,具有原理简单且容易实现的优点[18]。由此,在利用DASSA算法优化过程中,适应度函数可定义为目标函数加上罚函数,表示如下:
F(x)=J+P(x)
(25)
式中:J为目标函数,P(x)为罚函数,可表示为:
pb(x)+pf(x)]
(26)
式中:N为轨迹优化过程中的离散点个数,ph(x),pd(x),pl(x),pb(x)和pf(x)分别为超出热流密度、动压、过载、边界条件和终端状态约束的罚函数,定义如下:
(27)
(28)
(29)
(30)
(31)
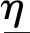
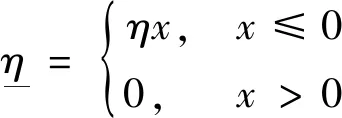
(32)
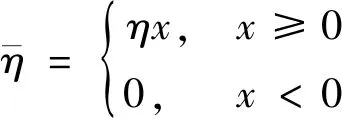
(33)
3.3 DASSAGPM算法的优化程序
针对高超声速飞行器再入轨迹优化问题,利用DASSAGPM混合优化算法求解最优控制量。具体来说,将整个优化过程分为两个阶段。在第一阶段,利用DASSA优化算法对控制量进行全局寻优,这样能充分利用智能优化算法的全局搜索能力,避免陷入局部最优。当适应度函数变化值达到预先设置的停止标准时,停止DASSA算法的寻优过程,并将求得的近似全局最优解作为GPM优化的初始猜测值。第二阶段,利用GPM对控制量进行全局寻优,这样便于利用GPM收敛速度快、精度高的优点。DASSAGPM优化算法的详细步骤如下:
阶段1:
1)将带复杂约束的高超声速再入轨迹优化问题公式化。
2)设定DASSAGPM优化算法的参数:最大迭代次数L,种群大小M,离散LG点数N,DASSA算法停止标准eDASSA,GPM算法停止标准eGPM。
3)将时间区间[t0,tf]用N个LG点等距离散。将控制变量u=[α,σ]T作为待优化的变量,每个种群个体的位置即代表一组控制变量的优化值。种群的完整信息可用矩阵表示为:
X=[X1,…,Xn,…,XN]
式中:离散点n的优化矩阵为:
式中:αnm表示第n个离散点上第m个种群个体寻优的攻角值,σnm表示第n个离散点上第m个种群个体寻优的倾侧角值。
4)在约束范围内随机初始化M个种群个体的位置。
5)基于种群个体的离散位置信息通过插值法计算连续控制量u,结合控制量对动力学方程(1)积分求得系统状态和状态的微分,接着计算每个种群个体的适应度函数值。
6)更新所有种群个体的位置,并更新全局最优值和局部最优值。
7)如果达到最大迭代次数或者DASSA算法停止标准eDASSA,则停止DASSA算法优化过程,并保存目前获得的最优控制量以及相关状态量,然后,进入8);否则返回5)。
阶段2:
8)将离散点处DASSA算法优化得到的控制量值作为GPM的初始猜测值。GPM优化过程中的相关参数,如变量范围、边界范围和离散LG点都保持不变。
9)通过GPM将再入轨迹优化问题转化为NLP问题后,利用NLP求解器求解。如果达到GPM算法停止标准eGPM,则停止GPM算法优化过程。
10)利用得到的最优控制量u*对动力学方程(1)积分求得系统状态量,由此可得再入过程中的最优控制变量和状态变量。
11)如果计算时间和代价函数值满足条件,结束仿真过程;否则,调整离散LG点数N并返回3)。
DASSAGPM算法的优化流程图如图1所示。需要指出的是,轨迹优化过程是离线完成的,DASSAGPM算法比GPM算法的步骤多,实际上并不会影响再入过程的实时性。另外,本文算法虽然是以高超声速飞行器为背景,针对在存在复杂约束条件下传统GPM算法在解决高超声速飞行器再入轨迹优化问题时对初始猜测值敏感的不足而提出的。但是,该算法本质上是一种优化方法,因此不仅仅适用于高超声速飞行器的再入轨迹优化问题,同时也适用于任何飞行轨迹优化甚至一般的优化问题。
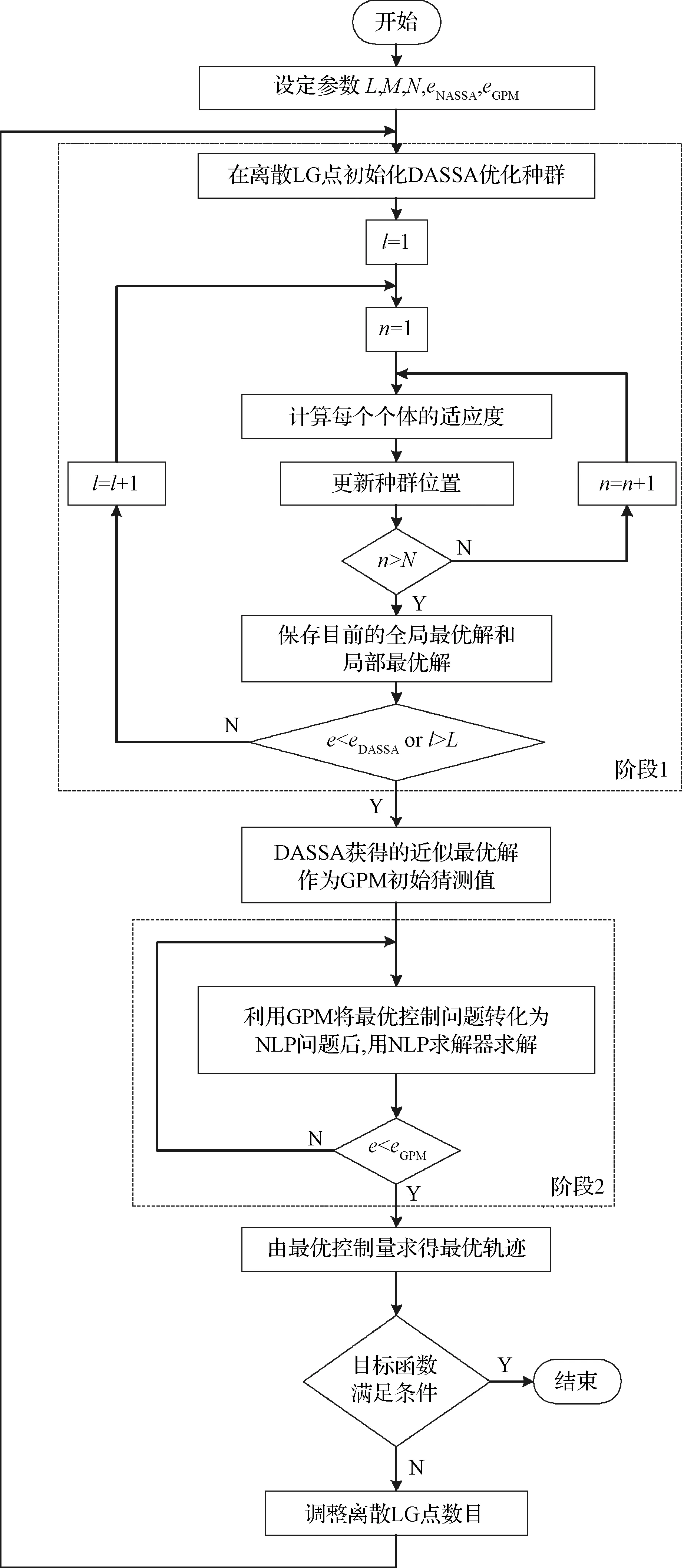
图1 DASSAGPM算法优化流程图Fig.1 Optimization flow chart of DASSAGPM algorithm
4 仿真校验
本节针对DASSA优化算法和DASSAGPM轨迹优化算法进行了大量的仿真,以验证所提算法的可行性和优越性。
4.1 DASSA的优化性能
为了验证DASSA算法的优化特性,利用DASSA算法对文献[13]中的部分基准函数进行迭代寻优。作为比较,同时采用WOA、SSA、PSO和GWO对基准函数寻优。为保证对比的公平性,统一设置参数为L=500,M=30。表1给出了基准函数描述,其中,基准函数表达式为:
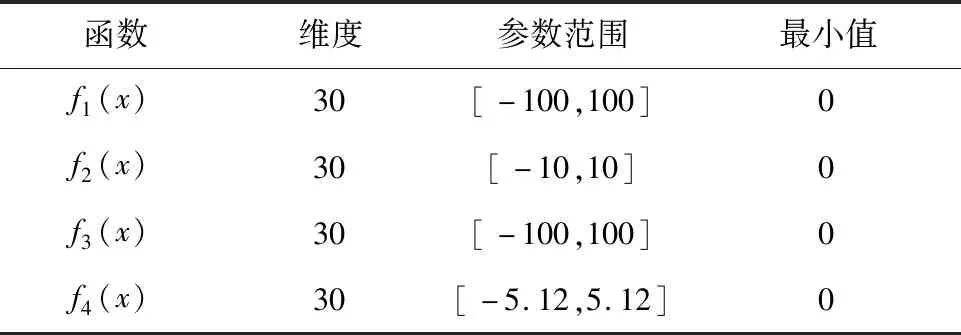
表1 基准函数Table 1 Benchmark functions
图2~图5给出了五种优化算法对基准函数优化过程中的函数值收敛曲线。可以看出,SSA和DASSA算法在收敛速度上具有明显优势,同时也更容易达到全局最优。进一步观察可知,由于在SSA算法中引入了动态自适应机制,使得改进后的DASSA算法在寻优过程中探索和利用的平衡更为合理,收敛速度和精度进一步得到改善。
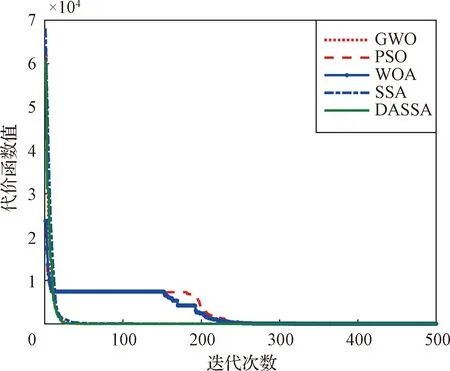
图2 f1优化过程Fig.2 Optimization process of f1 function
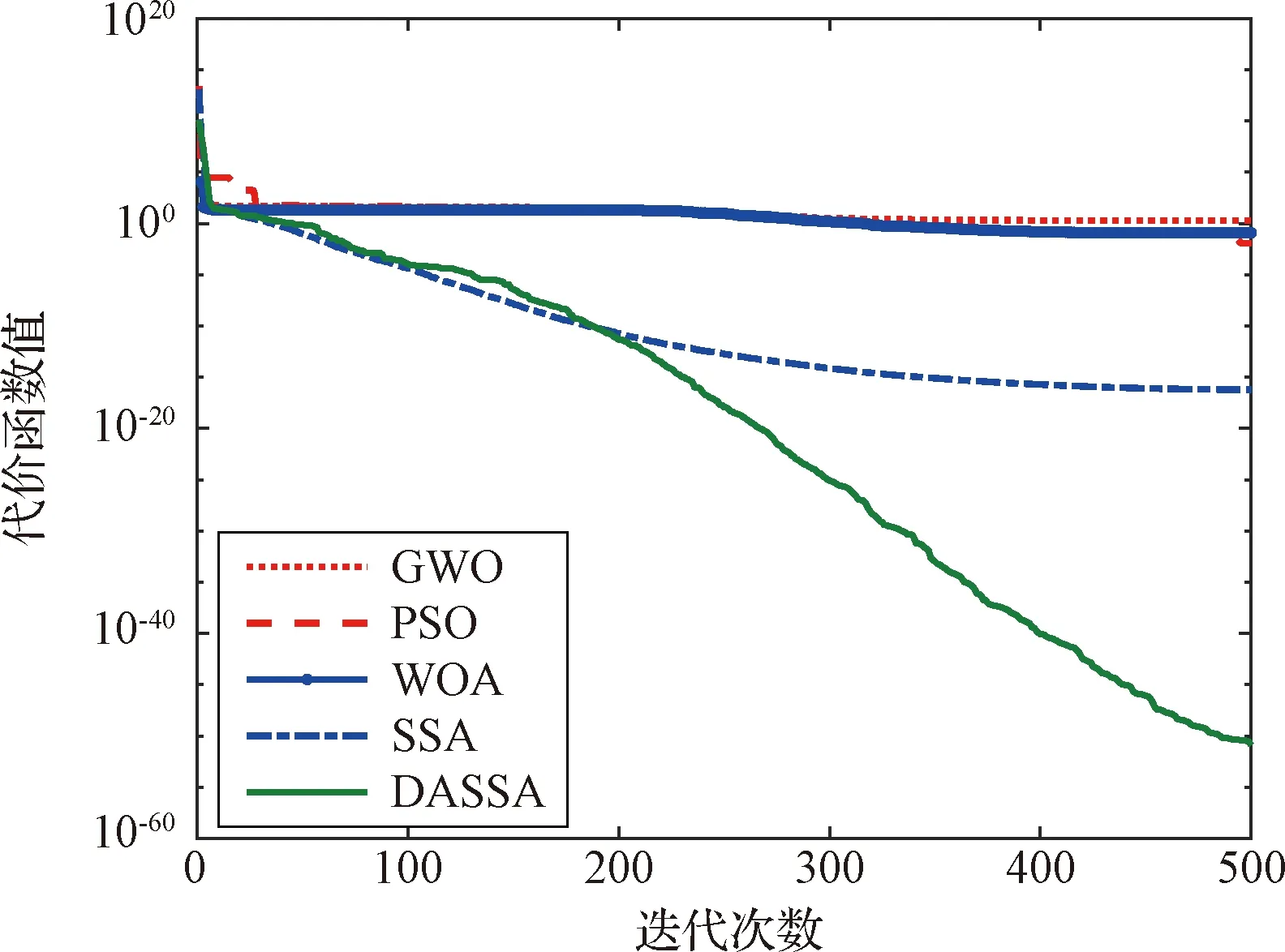
图3 f2优化过程Fig.3 Optimization process of f2 function
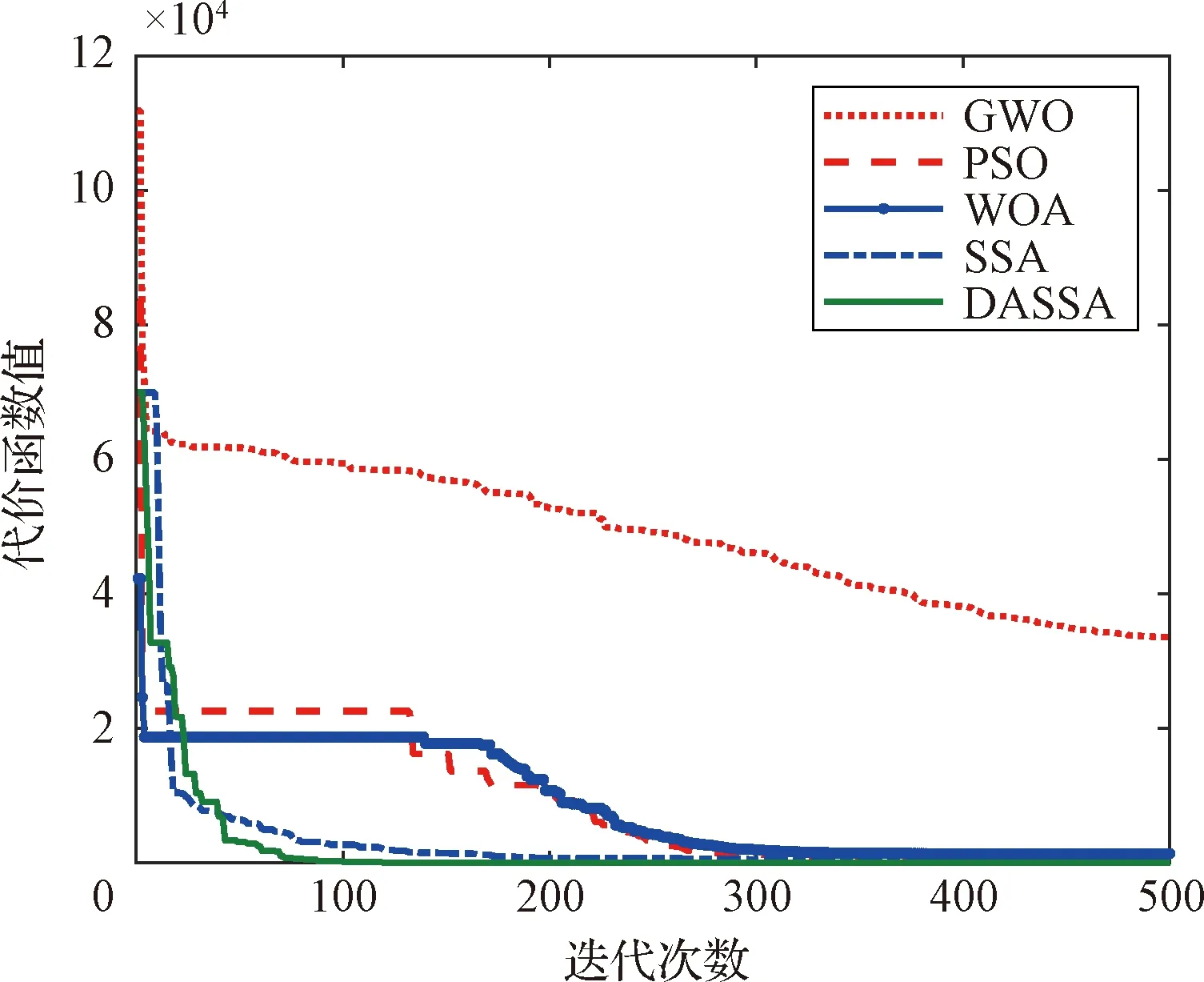
图4 f3优化过程Fig.4 Optimization process of f3 function

图5 f4优化过程Fig.5 Optimization process of f4 function
4.2 DASSAGPM的轨迹优化性能
本节将通过大量仿真验证DASSAGPM算法在飞行器轨迹优化上的优越性。在利用GPM进行轨迹优化时,本文采用开源软件GPOPS求解最优轨迹,其中SNOPT软件作为NLP求解器。为了展示DASSAGPM算法的优越性,将GPM、SSAGPM和DASSAGPM三种算法的轨迹优化性能进行对比。出于对比的公平性考虑,参数统一设置为L=500,M=40,N=31,eSSA=eDASSA=100,eGPM=1×10-5。热流密度约束为1.5 MW/m2,动压约束为200 kPa,过载约束为4.5g。状态变量的初始值和终端约束如表2所示。
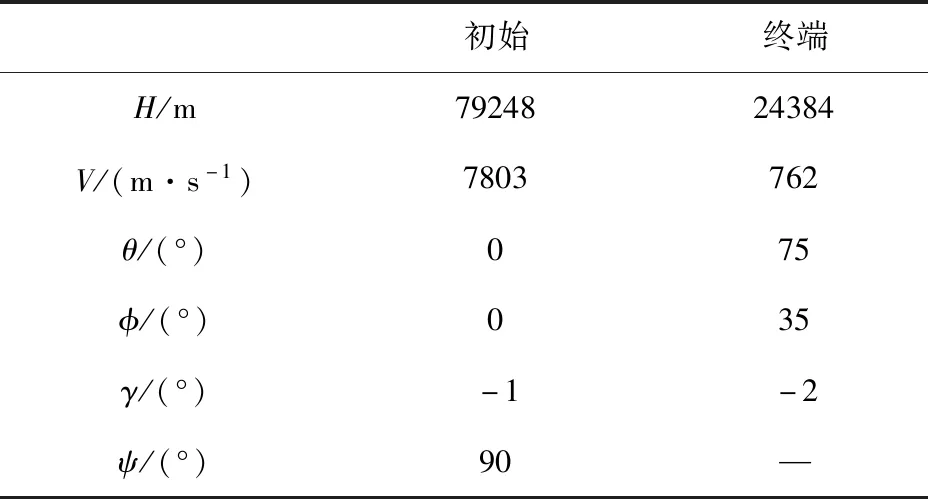
表2 状态变量的初始值和终端约束Table 2 Initial values and terminal constraints of state variables
图6~图9给出了飞行器再入过程中的三维轨迹、速度、航迹倾角和航迹偏角曲线,可以看出,三种算法均能使高度、经纬度、速度、航迹倾角和航迹偏角满足终端约束要求。进一步观察可知,GPM算法优化得到的轨迹跳跃最剧烈,SSAGPM次之,DASSAGPM算法的轨迹曲线最为平滑平缓,说明DASSAGPM算法的优化解最接近全局最优解,代价函数值最小。
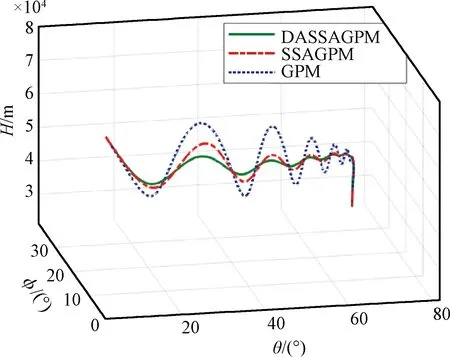
图6 三维轨迹曲线Fig.6 Three dimensional trajectory
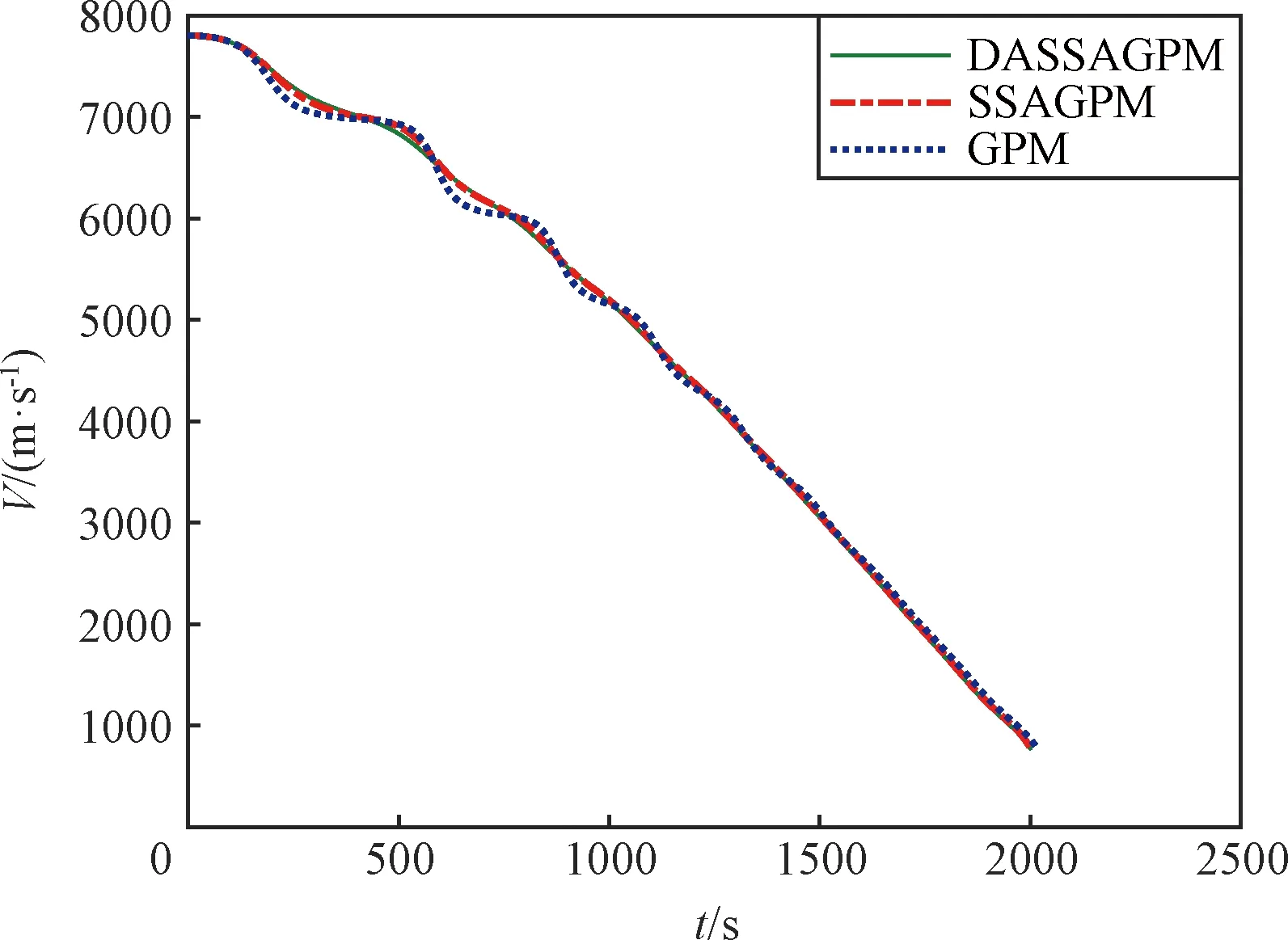
图7 速度曲线Fig.7 Velocity profile
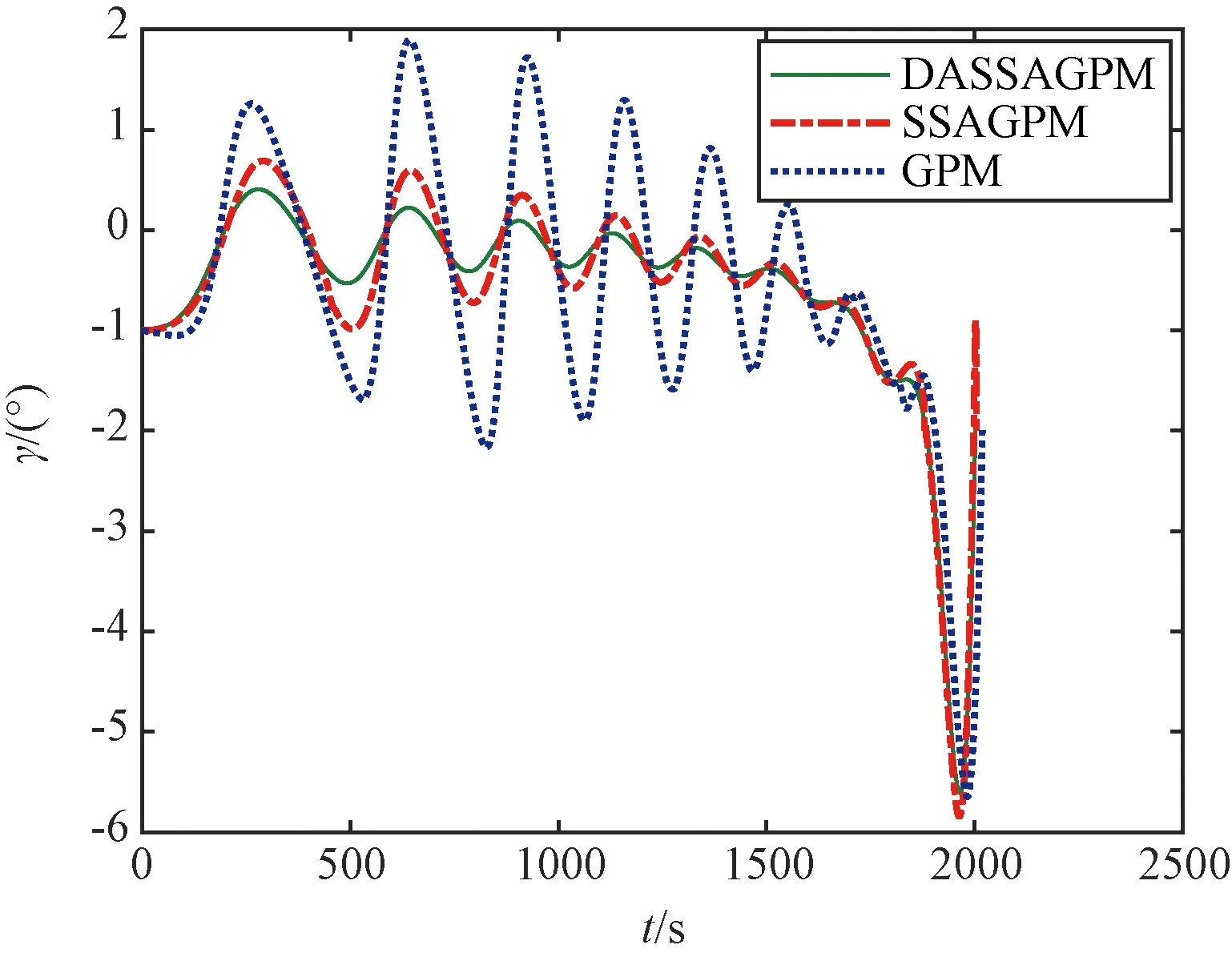
图8 航迹倾角曲线Fig.8 Flight-path angle profile
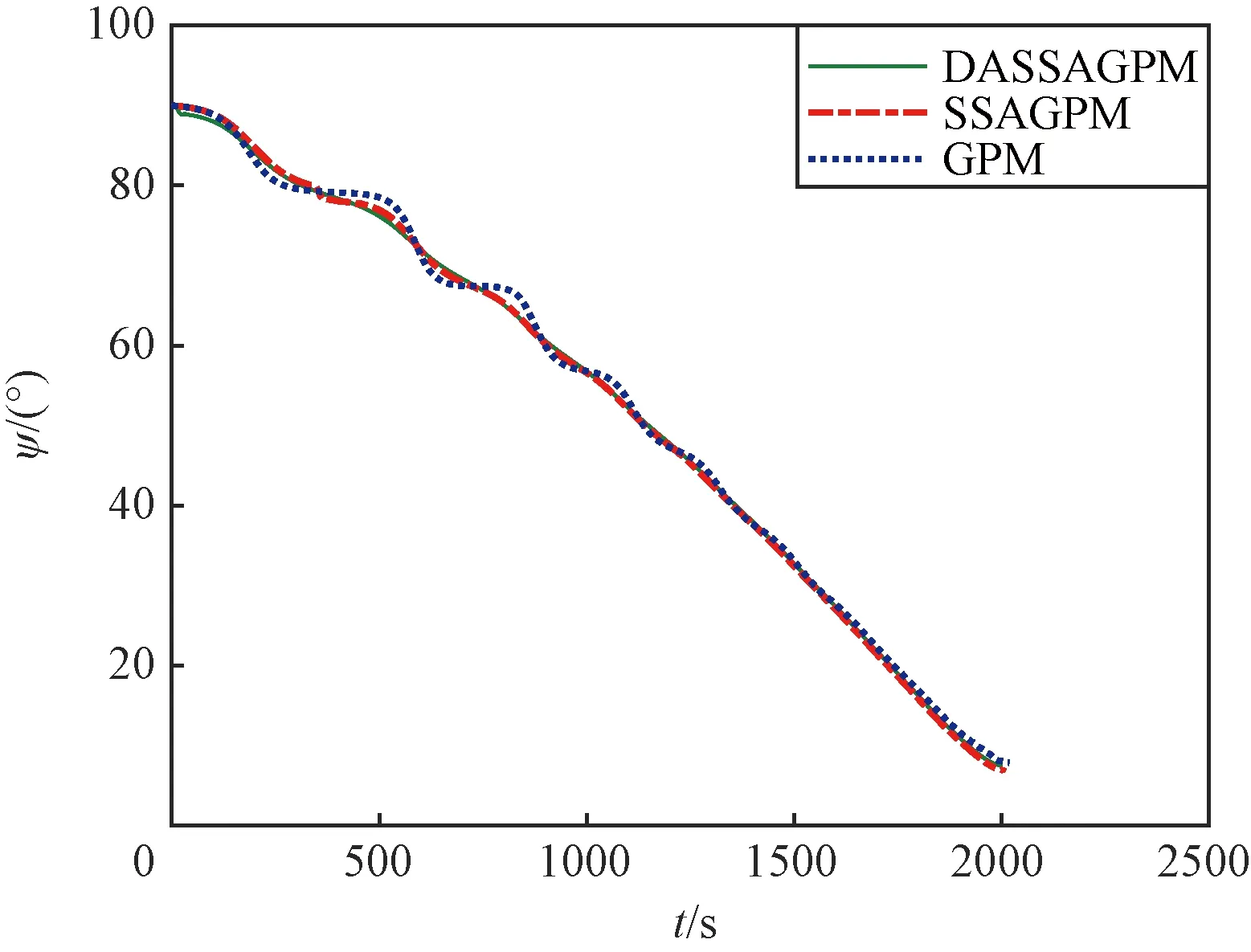
图9 航迹偏角曲线Fig.9 Heading angle profile
图10和图11分别给出了控制量攻角和倾侧角的曲线对比。可以看出,三种优化算法的控制量都在控制边界内,DASSAGPM算法优化得到的控制量最光滑,而GPM算法的控制量最不光滑。
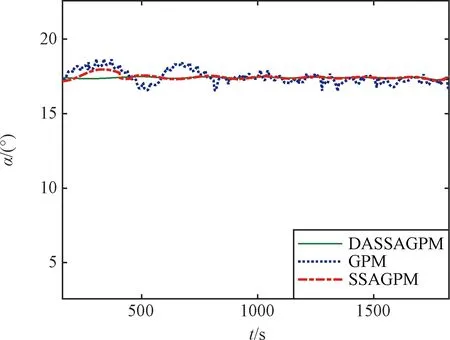
图10 攻角曲线Fig.10 Angle of attack profile
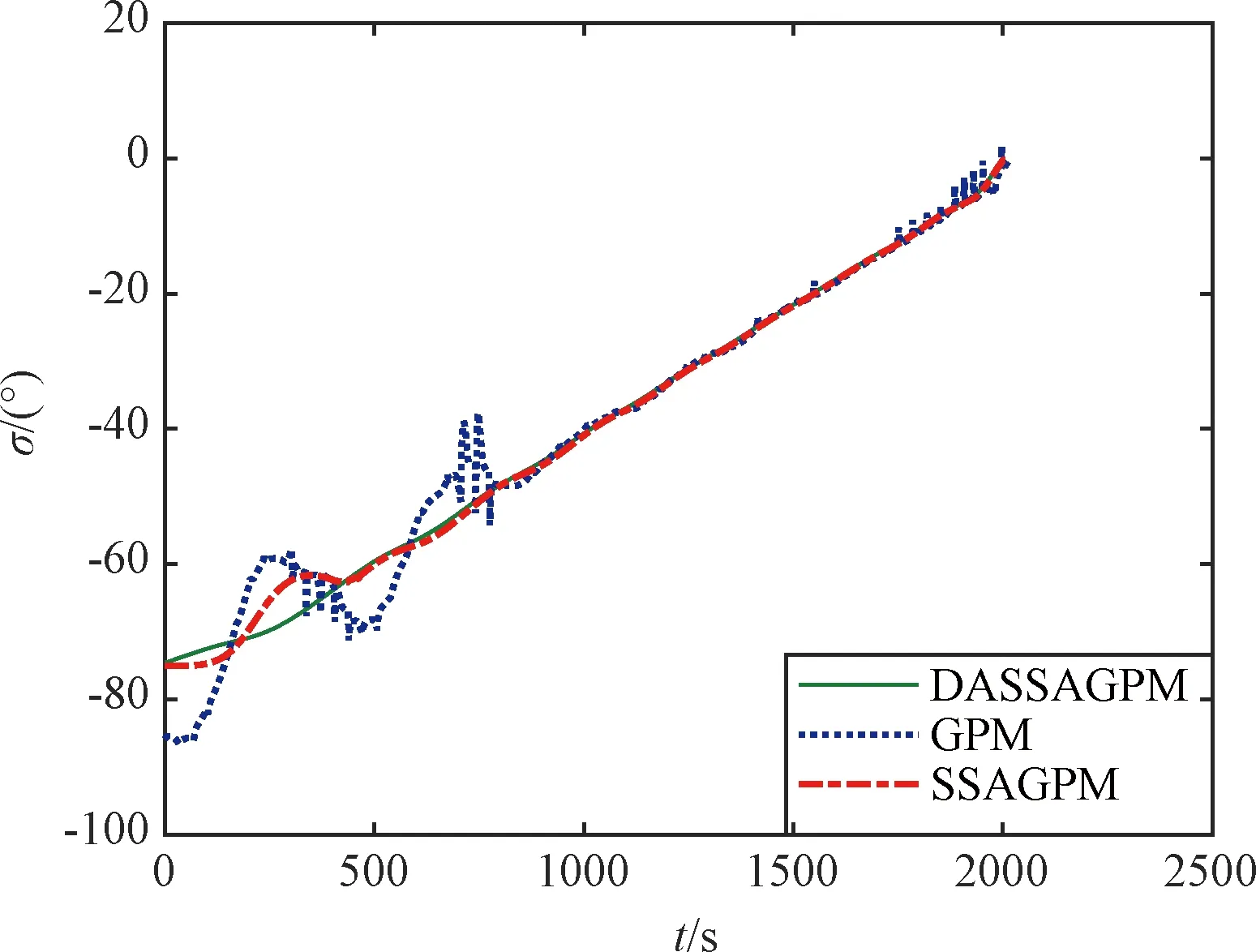
图11 倾侧角曲线Fig.11 Bank angle profile
图12~图14分别给出了三种算法的热流密度、动压和过载曲线对比,可以看出均满足约束条件,其中DASSAGPM算法的振幅最小,再入过程中的热载最小,优化效果最好。
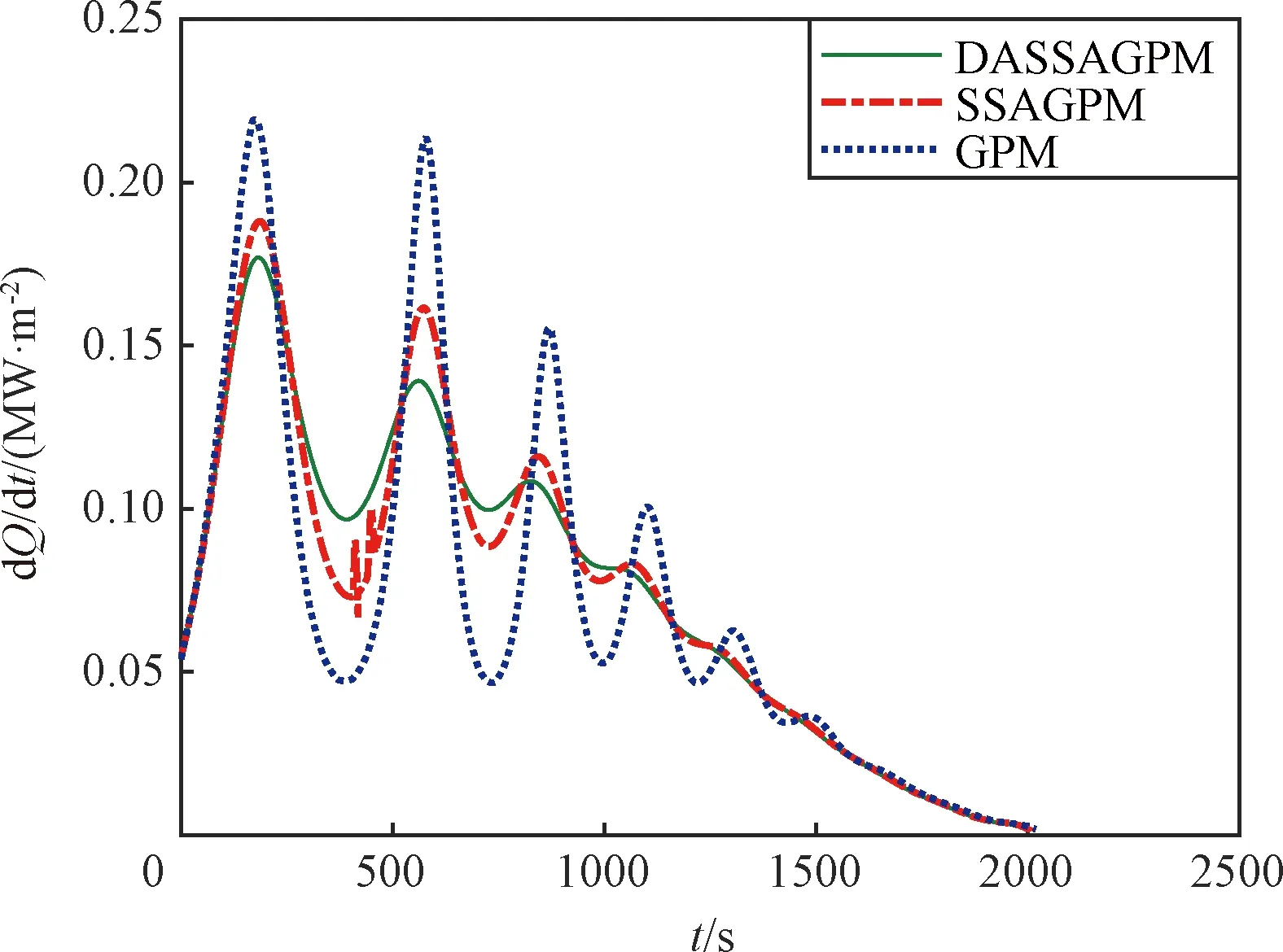
图12 热流密度曲线Fig.12 Heat flux density profile

图13 动压曲线Fig.13 Dynamic pressure profile
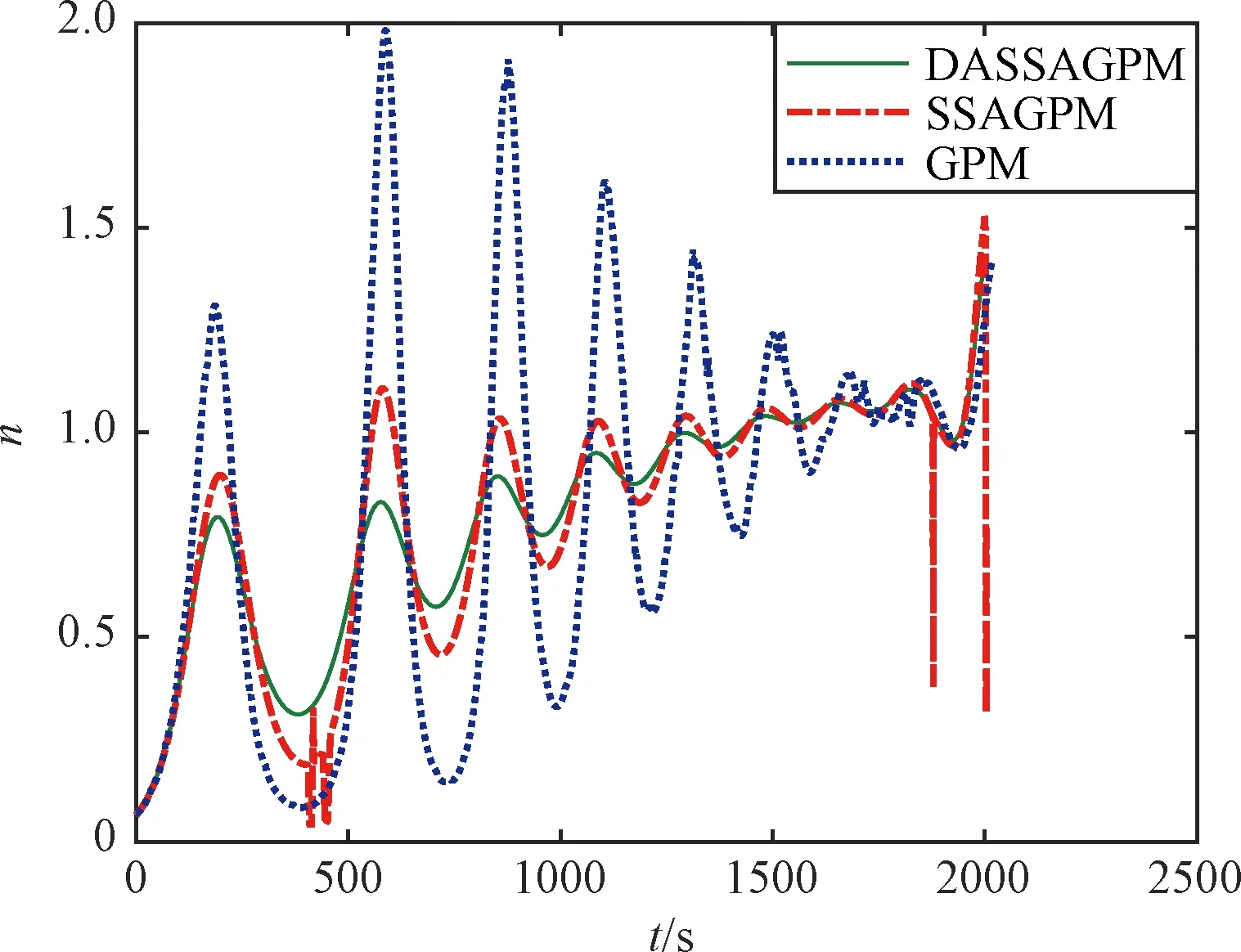
图14 过载曲线Fig.14 Overload profile
为了进一步验证DASSAGPM算法在轨迹优化方面的优越性,对三种算法进行50次蒙特卡罗仿真试验,所得到的代价函数值如图15所示。可以明显看出,DASSAGPM算法的全局寻优能力最强,整体代价函数值最小,次好的是SSAGPM算法,相比之下,GPM算法的全局寻优能力最差。表3给出了代价函数值统计数据对比,DASSAGPM算法的代价函数值均值最小,全局寻优能力最好。
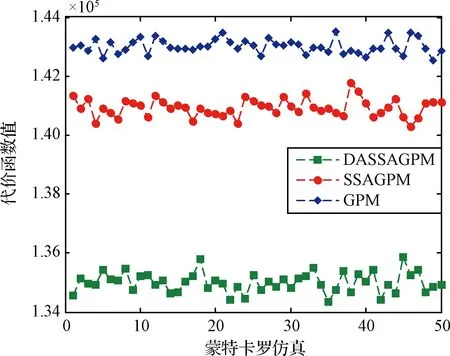
图15 蒙特卡罗仿真代价函数值曲线Fig.15 Fitness value curves of Monte Carlo simulation
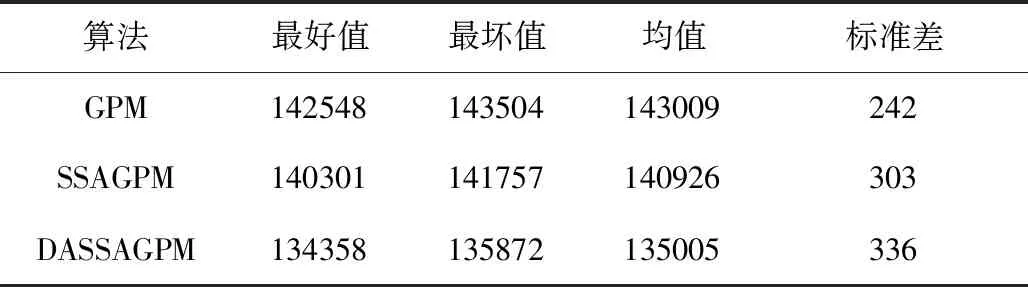
表3 代价函数值统计Table 3 Fitness value statistics
5 结 论
针对高超声速飞行器面临复杂的再入环境以及大的不确定性下的轨迹优化问题,提出了一种基于DASSAGPM算法的解决方案。
1)为了使SSA优化算法探索和利用之间的平衡更加地合理,提出了一种新颖的DASSA优化算法。仿真结果表明DASSA算法在基准函数优化上具有收敛速度快、更易获取全局最优值的特点。
2)在利用DASSA算法进行轨迹优化时,采用罚函数法处理再入过程中的各种约束。
3)针对传统GPM在轨迹优化过程中对初始猜测值敏感的不足,借助DASSA算法强大的全局搜索能力,提出了DASSAGPM再入轨迹优化方法。仿真结果表明所提出的DASSAGPM算法在求解再入轨迹优化问题时收敛速度快、精度高且更容易搜寻到全局最优解。
