地月空间NRHO与DRO在月球探测中的应用研究

2020-08-11李朝玉

宇航学报 2020年7期

曾豪，李朝玉,彭坤,王平，黄震

(1.中国空间技术研究院载人航天总体部，北京100094；2.北京理工大学宇航学院，北京100081)

0 引言

地月系统平动点轨道是空间环境观测与行星际探测任务的低能量枢纽[1-2]。ARTEMIS任务利用地月Lissajous轨道研究了地球磁尾与太阳风的相互作用[3]。“嫦娥5T1”服务舱[4]实现了利用月球近旁飞越进入地月平动点轨道，促成了“嫦娥4号”中继星的L2点Halo轨道任务，为着陆器与巡视器的月球背面任务提供了导航方案[5]。其次，NASA提出的“月球轨道平台门户”计划[6]，将空间站部署于月球附近的近直线Halo轨道(Near rectilinear Halo orbit, NRHO)，能够作为未来地月空间物资运输访问、火星探测和载人小行星任务的中转站。由于平动点轨道存在的诸多优点，如何实现探测器低能量往返转移轨道设计成为空间领域研究的重点与难点。同时，低能量轨道源于多天体系统下引力的共同作用，在轨道设计时将面临复杂动力学环境的影响，针对此背景，对地月空间三体轨道在月球探测中的应用研究是必要的。

针对地月空间轨道设计问题，转移方式主要分为直接转移、弱稳定转移、借力转移与小推力转移。Rausch[7]采用两层微分修正算法构造了地球停泊轨道与L1点Halo轨道的两脉冲直接转移，但直接转移所需速度增量较大。Zanzottera等[8]与Parker等[9]提出弱稳定边界转移策略，通过连接地月空间与日地空间的流形结构，系统分析地月L2点Halo轨道的转移特性，而弱稳定转移存在着任务时间长等问题。

Gordon将流形理论与借力技术相结合，设计了不同幅值Halo轨道两脉冲转移轨迹。针对Gordon研究中借力点方位不可调与燃耗较大等局限性，Li等[10]、Folta等[11]与Zeng等[12-13]对月球借力方位与入轨点位置进一步研究，提出了改进的月球引力辅助三脉冲转移方案，并给出了入轨点选择策略与定量分析月球借力约束集合的影响。同时，随着小推力技术日趋成熟。Ozimek等[14]、Zhang等[15]基于不同的优化策略，对地月空间小推力转移轨迹进行求解，实现了不变流形与小推力轨道的最优拼接。

在地月空间任务中引入天体借力飞行，能够有效地降低轨道转移的燃料消耗。然而，借力天体附近动力学环境的多样性与复杂性，给轨道最优借力点的确定带来了挑战。同时，不同目标轨道及入轨点位置的选取，一定程度影响着转移轨道的燃料性能指标。因此，如何建立合适的借力约束模型，如何将借力技术与二体Lambert转移有效融合，如何调整入轨点保证低燃耗的同时降低任务时间，都是天体引力辅助轨道设计时需要考虑并解决的问题。

本文针对上述问题，采用遗传算法与二体Lambert转移初值搜索策略，快速确定满足约束的轨道初值。基于序列二次规划算法(SQP)与多重打靶法，构造出同时考虑近月点与近地点等约束的燃料最优地月往返转移轨道。其中，引入时间变量表征目标轨道，能够在求解过程中搜索确定往返轨道合适的入轨点与逃逸点。选取三体轨道NRHO与DRO为研究对象，重点分析了不同近月点高度、目标轨道空间结构对任务时间与机动速度增量的影响。最后，通过关键数据对比，突出本文设计策略的适用性与有效性，在未来的月球探测任务中提供借鉴与技术支持。

1 轨道动力学模型及研究对象

1.1 圆型限制性三体模型

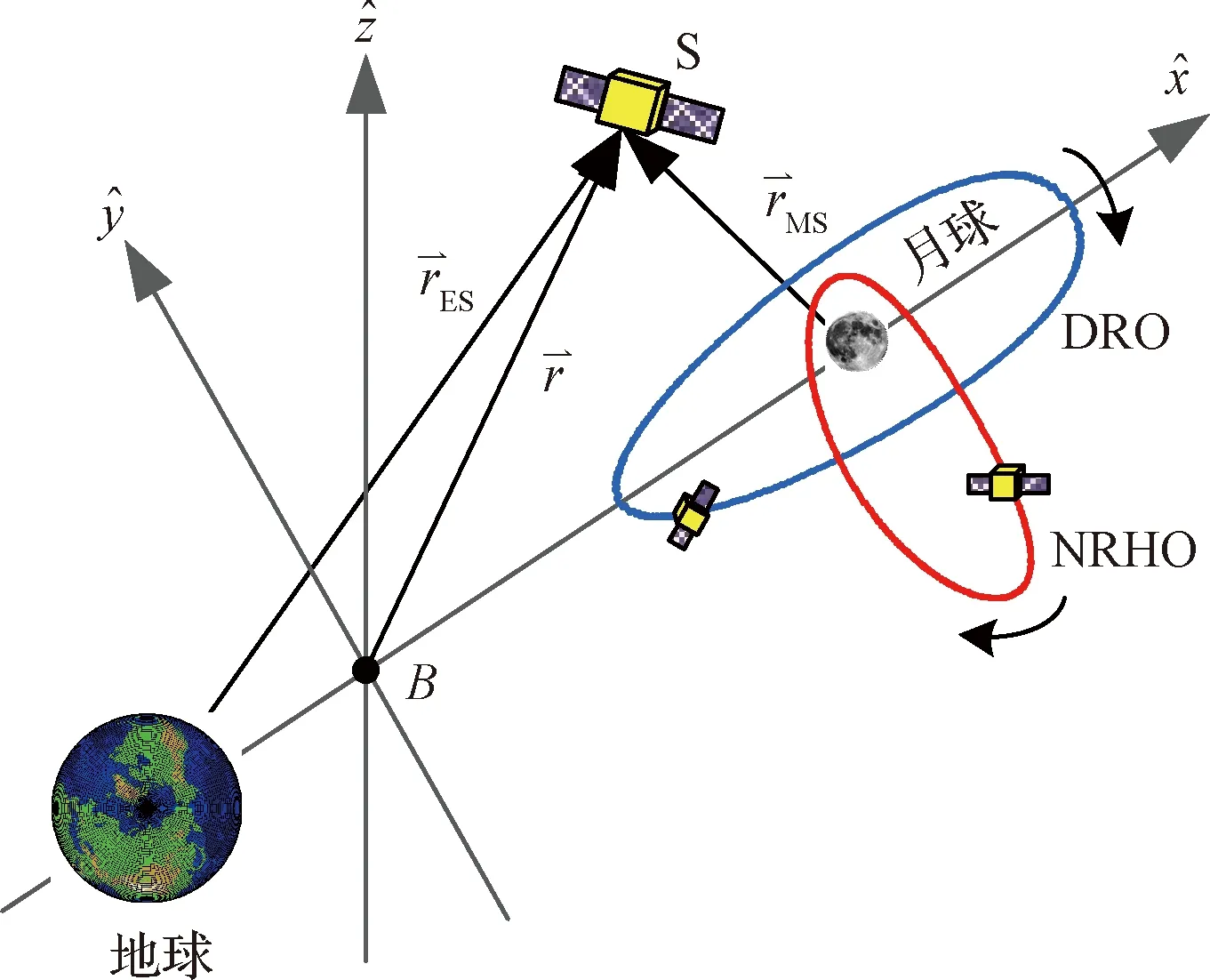
图1 质心旋转坐标系及目标轨道Fig.1 Rotating barycenter frame and target orbits

在质心旋转系中，飞行器的动力学方程为：

(1)

其中，

(2)

文中利用雅克比常数C表征所考虑的周期轨道，积分常数满足：

(3)

1.2 目标轨道及状态转移矩阵

圆型限制性三体模型中存在着不同类型的周期轨道与拟周期轨道。文中主要针对近直线Halo轨道，即“月球门户”计划的目标轨道NRHO，与大幅值逆行轨道(Distant retrograde orbit, DRO)两种类型的地月往返轨道特性进行研究，如图2所示。

NRHO是一类在地月三体系统中，由L1点和L2点附近Halo轨道演变形成，并且轨道周期较短的三体轨道。飞行器借助月球引力辅助进入NRHO所需的速度增量较小。由图2(a)可知，NRHO近月点距离月球较近，能够较好地支持月球极区的探测。

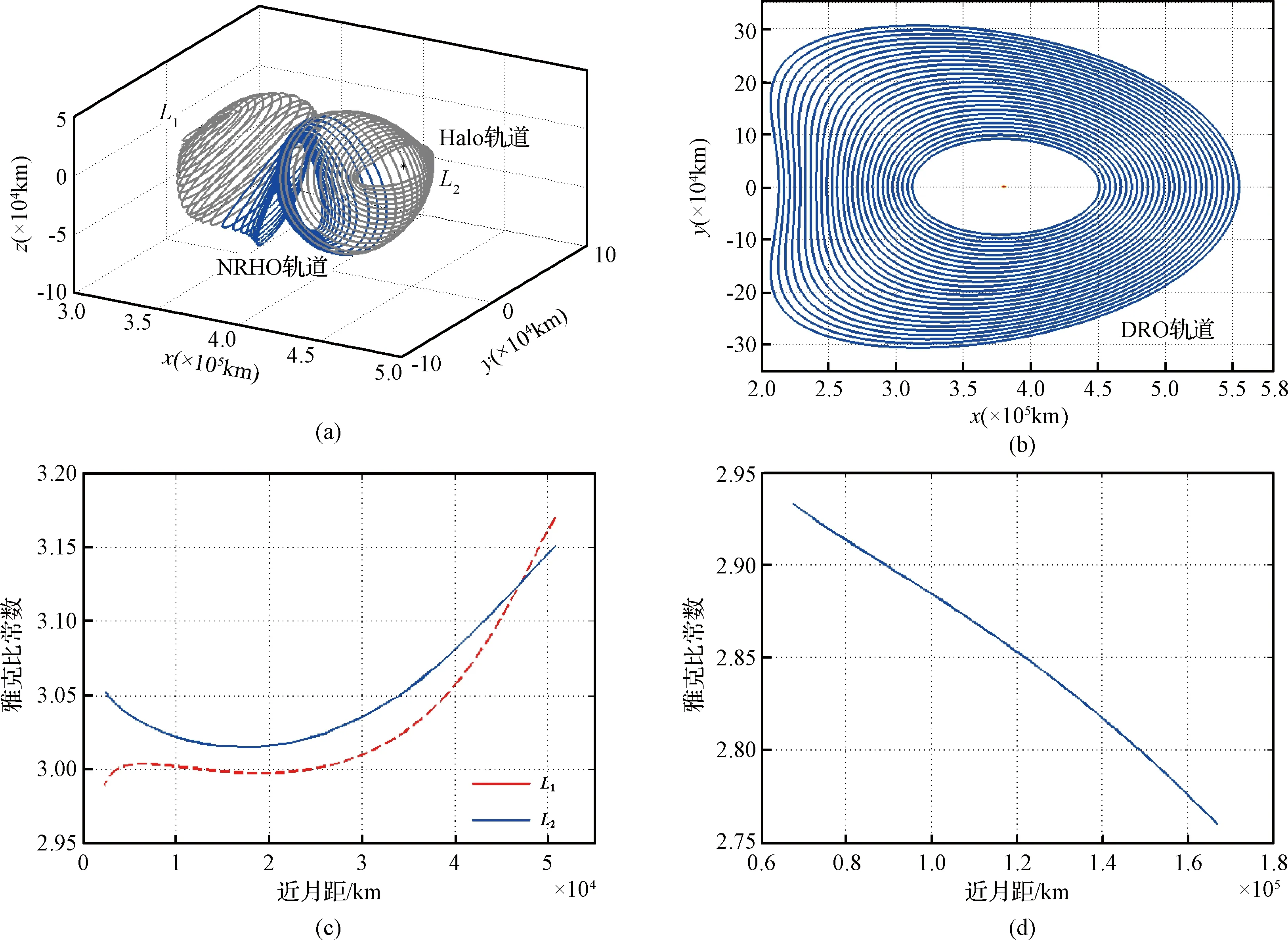
图2 地月系统目标NRHO与DRO空间分布Fig.2 Map of NRHO and DRO in Earth-Moon system

DRO属于逆行环绕月球的共振周期轨道。研究表明，DRO相对稳定，放置于此轨道上的飞行器能够长期保持稳定。此类型轨道主要运用于日地观测与小行星访问任务，作为小行星捕获的中转站。

在CRTBP模型中，通过状态转移矩阵能够联系当前时刻与下一时刻的状态量，降低轨道设计的难度，即：

(4)

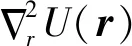
2 约束建模与转移方案分析

2.1 借力约束模型的定义

针对地月空间NRHO与DRO往返轨道设计，本文考虑月球引力作用以降低任务的燃料消耗，飞行器由地球出发飞抵目标轨道的转移轨迹如图3(b)所示，其中圆点为轨迹拼接点。

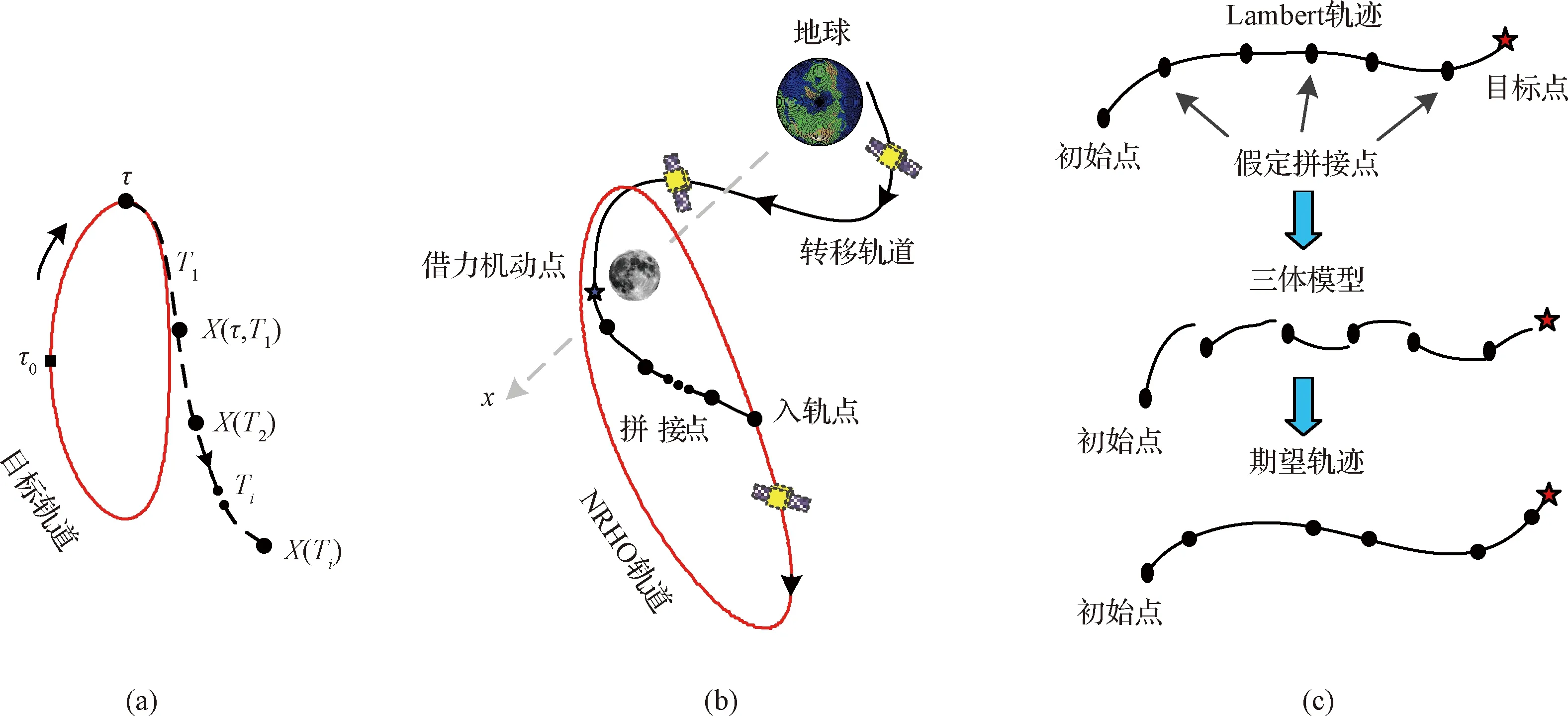
图3 借力转移示意图、设计变量及多重打靶法Fig.3 Diagram of mission scenario, design variables definition and multiple shooting method

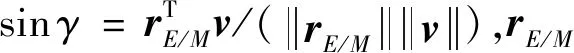
针对借力机动点与目标轨道之间的转移轨道段，为了较好地构造出满足约束的最优轨迹，采用多重打靶法对轨道分段处理，降低参数敏感性。因此，此轨道段自由变量C1包含入轨点三轴速度增量ΔVOI、各拼接点间飞行时间Ti与状态量Xi，以及目标轨道时间变量τ；针对近地点与借力点间轨道段，自由变量C2包含借力机动增量ΔVFB与地月转移时间TEM，则自由变量集合为：

C=[C1,C2]T=[ΔVOI,T1,…,Tn-1,

X2,…,Xn,τ, ΔVFB,TEM]T

(5)

约束方程表示为：

(6)

2.2 轨道初值搜索策略

针对轨道设计初值猜想问题，由于NRHO与DRO轨道相对稳定，无法通过不变流形构造轨道初值。本文采用轨道分段初值猜想搜索策略，将任务轨道分为地月转移段与月球-目标轨道段，能够有效地降低轨道设计对关键参数的敏感度，快速求解初值。其中，地月转移段参见文献[12]，主要针对月球-目标轨道段进行初值构造。以飞行器由地球飞抵目标轨道为例，返回轨迹设计方法类似。具体地：

结合遗传算法与Lambert理论快速求解近月点与入轨点间两点边值问题。其中性能指标函数为

(7)

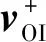
(8)

式中:TMH为此轨道段的飞行时间，根据任务指标要求与目标轨道空间位置确定搜索范围，本文假设TMH-NRHO∈(0.4, 1)天，TMH-DRO∈(6, 14)天。(rm,vm)为会合系下近月点状态量。通过遗传算法能够有效地搜索确定目标轨道上合适的入轨点，即自由变量τ。

2.3 约束方程解析梯度

上述搜索策略仅用于确定轨道设计初值与多重打靶法拼接点的大致区域，不能保证转移轨道的最优性，需要结合SQP算法进一步优化求解自由变量，确定燃料最优转移特征点位置，优化目标函数为：

(9)

自由变量与约束方程如式(5)～(6)所示。为了提高轨道设计的正确性与计算效率，推导了目标函数与约束方程关于自由变量的解析梯度。由于目标函数仅为ΔVOI与ΔVFB的函数，则

(10)

近月端高度与航迹交约束偏导数满足：

(11)

(12)

式中：rLF为近月点相对于月球质心的位置矢量，即rLF=rn-[1+μ,0,0]T。

近地点高度的微分关系满足：

(13)

(14)

(15)

航迹角约束的偏导数表示为：

(16)

式中:Φrr与Φrv为状态转移矩阵的3×3子矩阵，vsE与asE分别为旋转系下近地点速度与加速度矢量。近地点高度与航迹角约束关于状态量的偏导数与式(11)～(12)类似，只需将飞行器相对于地球的位置和速度矢量替换即可。

其次，拼接点状态量约束的梯度满足：

(17)

(18)

应注意，约束方程关于自由变量的解析梯度为(6n-2)×(7n+1)矩阵，相关项由式(11)至式(18)组成，其余项为零。

3 地月空间往返轨道特性分析

在地-月圆型限制性三体模型中，结合所提的设计策略，对不同结构的NRHO与DRO的月球借力往返转移轨道进行设计，分析幅值变化(即不同雅克比常数)对任务燃料与时间的影响，讨论转移轨道入轨点与借力机动点分布特性。在设计过程中，假设飞行器逃逸与返回时近地点轨道高度为200 km，航迹角为0°。

3.1 地月NRHO往返转移方案分析

3.1.1近月点高度对借力效果的影响

图4描述了仅考虑月球借力高度约束下，目标轨道近月点高度100 km，远月点高度66000 km，轨道周期6天的NRHO (C=3.05804)月球借力转移轨道，速度增量、借力机动点方位参数变化如图5所示。其中，类倾角与类升交点赤经仅在旋转坐标系下求解，其定义与月心惯性系下环月轨道倾角与升交点赤经定义相似。由图可知，不同工况下飞行器的飞行轨迹具有相同变化趋势，借力机动点分布于以月球为中心的yz平面附近，月球借力能够显著地改变飞行器的运动方向。

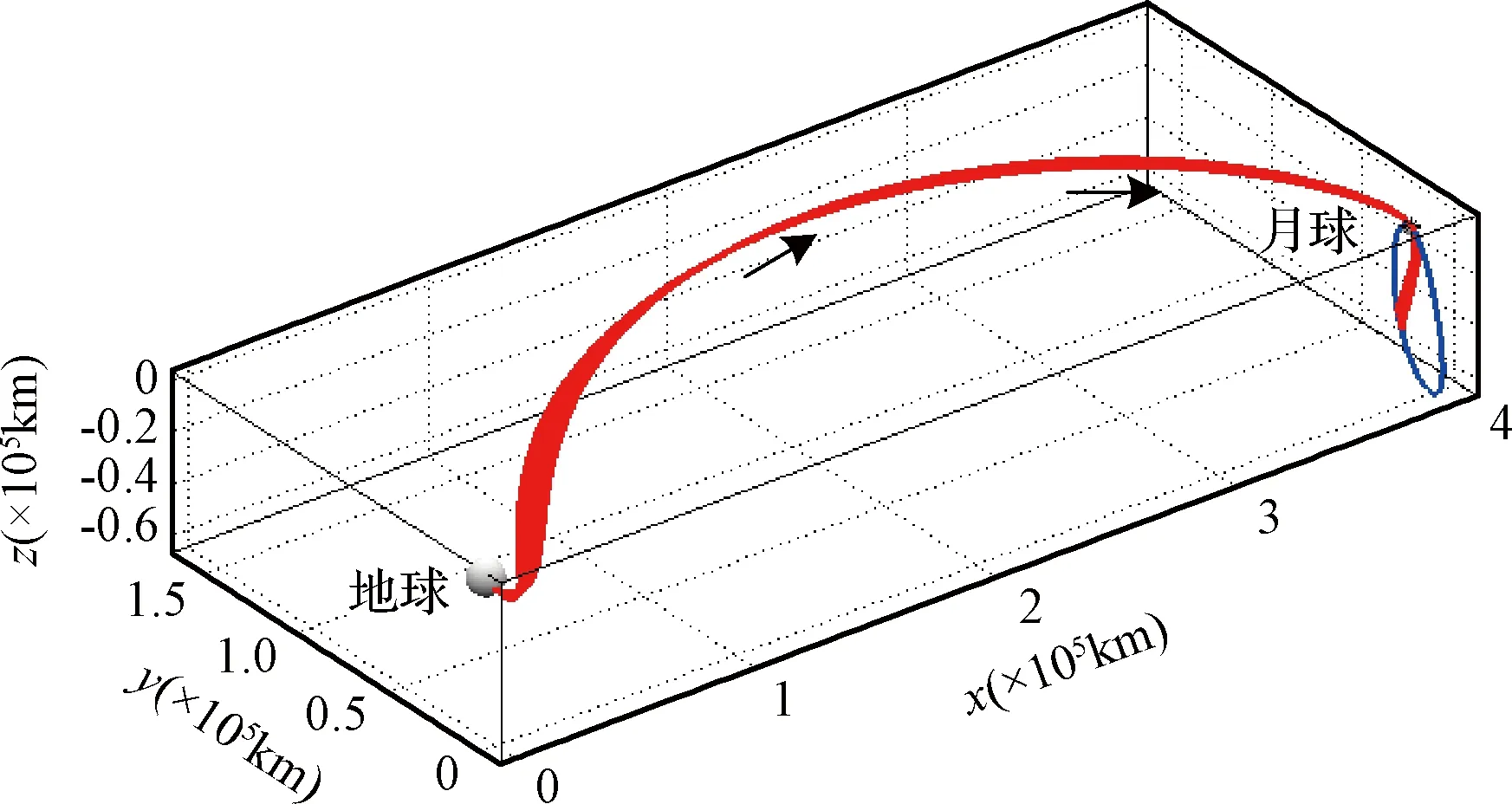
图4 不同近月点高度的NRHO最优转移轨Fig.4 The optimal transfers of NRHO with different flyby altitude constraints

由图5可知：1)针对NRHO转移方案，随着近月点高度不断增大，速度增量呈现先减小后增大的趋势，但不同近月点高度对任务机动增量影响较小，改变量仅为2.658 m/s，其中借力增量介于179.845 m/s与200.508 m/s，入轨机动保持在208.345 m/s至227.241 m/s之间;2)任务总飞行时间T∈(5.667, 5.832)天，相比于地月转移段，飞行器完成月球借力后，仅需约0.868天即可飞抵目标轨道; 3)不同工况下近月点对应的类升交点赤经与类倾角改变较小，类升交点赤经与类倾角范围分别为(90.438°，91.976°)与(86.244°，86.611°)，即NRHO转移的最优借力点位于月球极区附近。

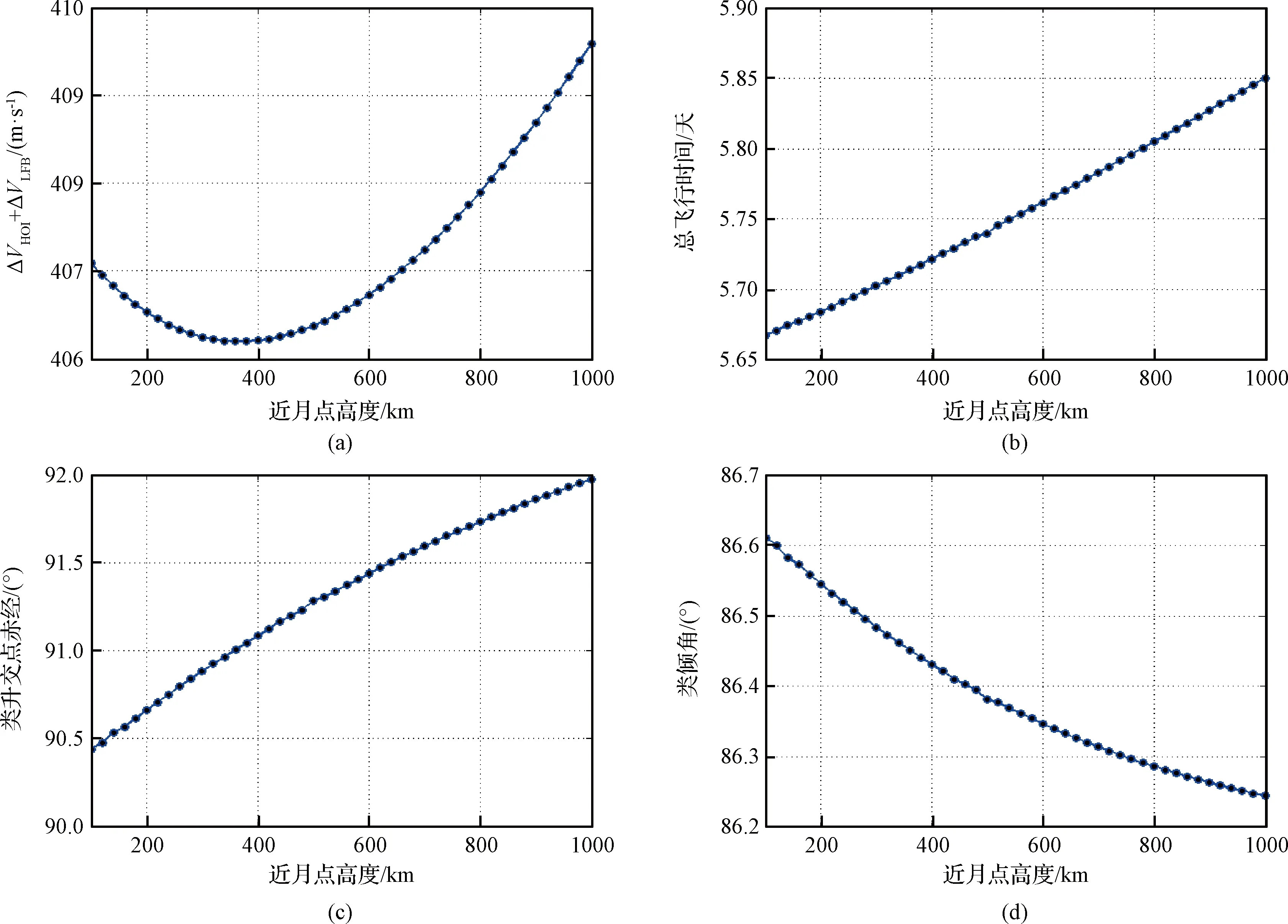
图5 不同借力高度的速度增量、飞行时间、类升交点赤经与类倾角变化曲线Fig.5 The curves of speed increment, flight time, analogy RAAN and inclination with different altitude

具体地，针对近月点高度360 km工况的最优转移，飞行器由地球停泊轨道出发，经过4.896天飞抵近月点，沿三轴施加速度增量ΔVFB=[11.263, -118.131, -144.069] m/s，即186.648 m/s完成月球借力操作，继续航行0.817天后到达目标NRHO，入轨机动为219.546 m/s。任务总飞行时间与燃料消耗分别为5.713天与3523.223 m/s。

对比分析借力转移与直接转移方案，直接转移速度增量特性如图6所示。直接转移合适的入轨点位于NRHO的远地点附近，随着目标轨道雅克比常数的逐步增加，捕获速度增量总体保持单调递增变化，介于793.216 m/s至847.332 m/s。其中，相应的转移时间改变量仅为0.5天，即时间范围为(5.171，5.674)天。比较图5与图6可知，飞行器采用借力转移方案所需的速度增量显著优于直接转移，而两种方案的飞行时间相差在1天内。

具体地，针对目标轨道雅克比常数C=3.05804的转移设计，飞行器直接转移机动增量为847.331 m/s，相应的转移时间为5.174天。而借力转移方案的总速度增量减少约441.138 m/s，时间仅增加5.713-5.174=0.539天。因此，基于月球借力的NRHO转移更具优势。

3.1.2NRHO的往返转移轨道特性分析

针对地球与不同尺寸的NRHO轨道之间的往返飞行轨道特性进行分析，飞行器往返轨道如图7所示，往返速度增量与飞行时间变化曲线如图8所示。其中，雅克比常数在[3.05776, 3.01566]内每隔0.001进行取值，最小值与最大值对应的近月高度与远月高度分别为120 km、65831 km与13669 km、83050 km。

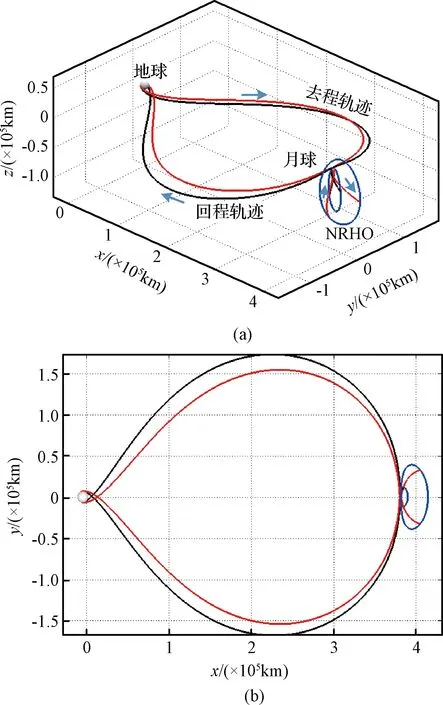
图7 NRHO空间往返转移轨道与平面投影图Fig.7 Round-trip transfer orbit of NRHO and the corresponding plane projection

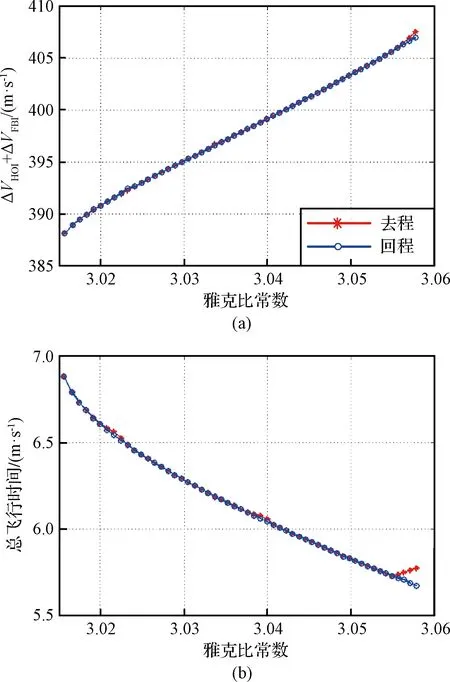
图8 不同工况下NRHO往返速度增量与时间特性Fig.8 The characteristics of speed increment and flight time of NRHO mission in different conditions

比较往返轨道及各项关键参数可知，不同工况下往返转移轨迹具有近似对称特性，各个特征点与各飞行时间参数相近。同样地，往返轨迹合适的月球借力位置位于极区附近。入轨点与借力点总速度增量大小随着雅克比常数的增大而增大，介于(388.099，407.499) m/s，而往返转移时间总体呈现下降趋势，改变量6.882-5.672= 1.210天。

当目标轨道C=3.05776 h，飞行器完成地球逃逸后，飞行4.999天后施加增量187.475 m/s完成月球借力机动，继续航行0.772天后抵达目标NRHO，入轨机动220.023 m/s。完成月球探测任务后，飞行器执行返回任务，在NRHO上施加227.454 m/s的速度增量完成离轨操作，航行0.728天后抵达近月点，执行机动179.497 m/s进行月球借力，改变飞行方向，随后继续运行4.944天返回地球附近。

当目标轨道C=3.01566时，往返各项关键参数满足：近月机动164.999 m/s与164.998 m/s，NRHO捕获与离轨223.101 m/s与223.100 m/s，地月段时间4.786天及4.787天。

3.2 地月DRO往返转移方案分析

飞行器往返于地球与DRO的转移轨迹如图9所示，对应的速度增量与飞行时间变化关系在图10中给出。与NRHO轨道结构相似，DRO往返轨道在平面内关于y轴具有对称特性。同时，飞行器航行于地球与目标DRO之间特征点总速度增量与飞行时间相差较小。随着雅克比常数的减小，能够更好地构造出低能量的转移轨道，但转移时间逐步增加，且近月点至入轨点转移段耗时较长。因此，可以根据任务对燃料与时间的要求对目标轨道进行选择。不同工况条件下，飞行器由地球出发，航行TEM∈(4.611, 6.679)天飞抵近月点时，需要施加142.453-176.962 m/s完成借力飞行，DRO入轨增量满足74.293 m/s与89.645 m/s范围内。

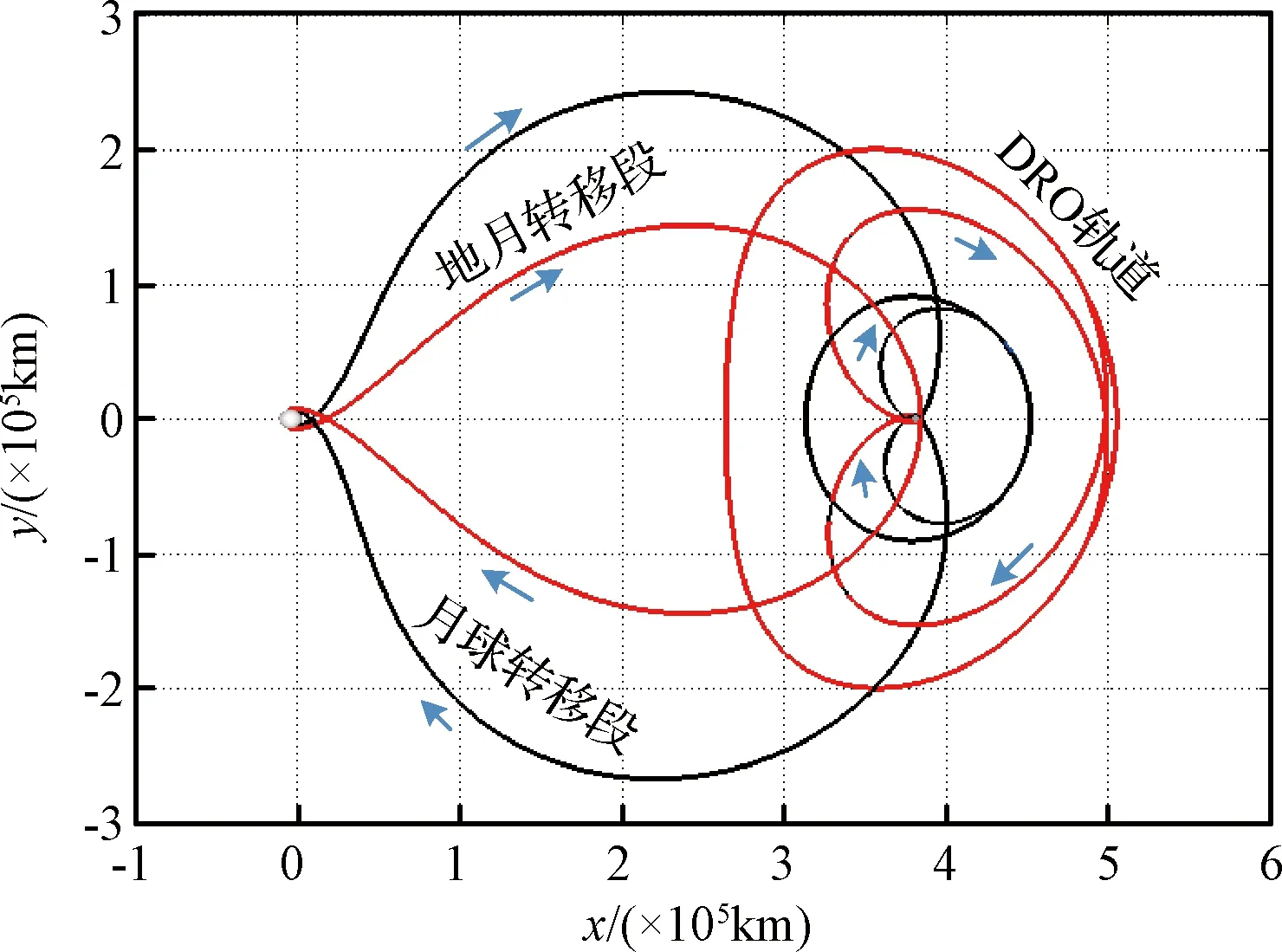
图9 地球-DRO空间往返转移轨道Fig.9 Round-trip transfer orbit between the Earth and DRO

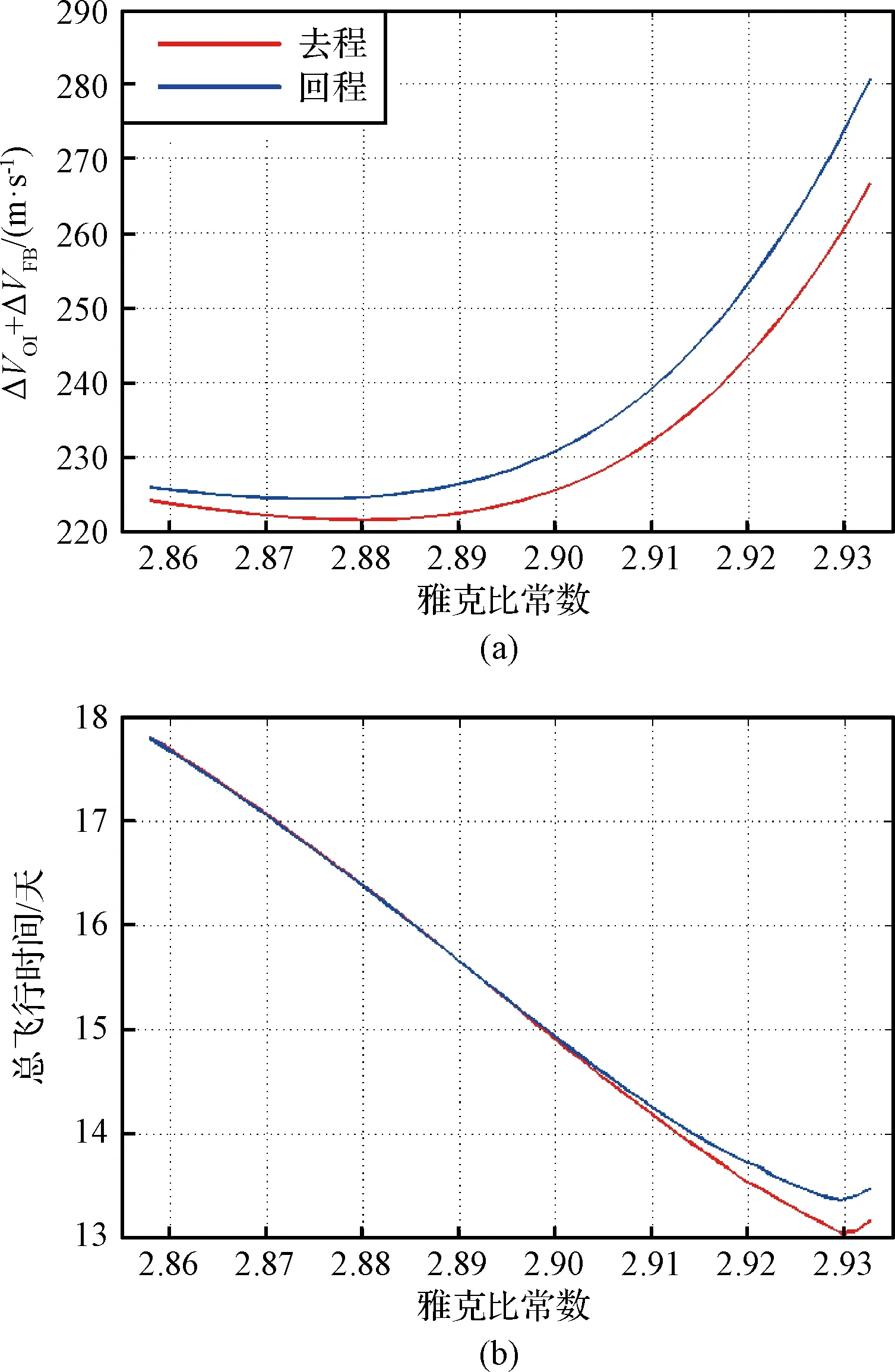
图10 不同工况下DRO往返速度增量与飞行时间曲线Fig.10 The curve graph of speed increment and flight time of DRO mission in different conditions

针对飞行器返回轨迹的速度增量与转移时间，与去程轨道数据比对可知，速度增量最大差值与最小差值分别为13.960 m/s(C=2.9326)与1.760 m/s(C=2.8578)。具体地，针对C=2.8578进行分析，飞行往返地月转移段时间约为4.636天，近月点机动增量分别为141.453 m/s与141.566 m/s，近月点至目标轨道段转移时间13.203天，完成DRO捕获与离轨增量为82.681 m/s与84.328 m/s。

其次，针对固定转移时间的地球至DRO任务参数特性进行分析，即13.559天，借力点机动与入轨点机动变化曲线如图11所示。由图可知，随着目标轨道雅克比常数的增大，入轨点速度增量不断减小，而借力点速度增量单调递增。入轨点机动是任务总速度增量变化的主要影响因素，即ΔVOI∈(89.859, 282.245) m/s，而借力机动改变量仅为15.987 m/s。

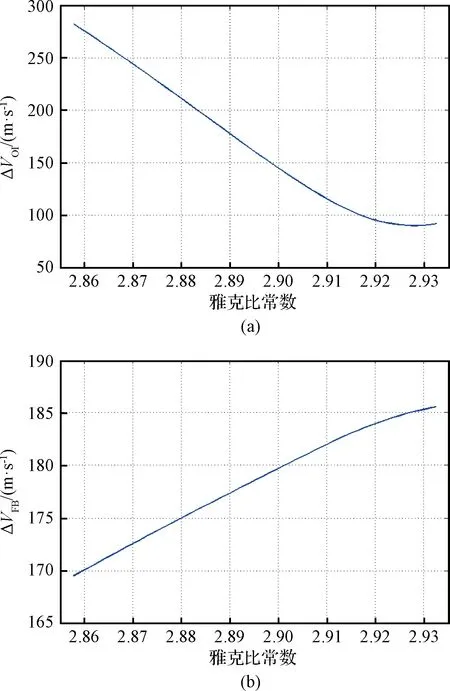
图11 固定时间的入轨点与借力点速度增量变化特性Fig.11 Variations of speed increment at flyby and insertion point at a fixed time

选取C=2.8578的DRO设计转移轨道，飞行器地月轨道段与月球-DRO轨道段时间分别为7.179天和6.380天。完成月球借力需施加169.536 m/s，而飞行器完成DRO捕获所需的速度增量较大，即282.245 m/s。与图10结果进行对比，固定时间转移任务的总飞行时间减小17.839-13.559=4.280天，相应的速度增量增大451.781-224.134= 227.647 m/s。因此，可根据任务指标要求，对方案的时间进行选择与设计。

3.3 关键参数对比分析

分析NRHO与DRO探月模式的速度增量需求与时间需求，同时将本文设计结果(图8(C=3.01566)与图10(C=2.8772)燃料最优数据)与以往研究中采用月球借力转移的数据进行对比，如表1和表2所示。

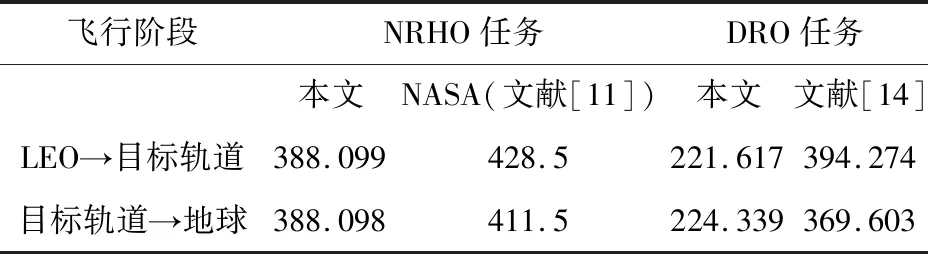
表1 不同探月模式的速度增量需求Table 1 Requirement for delta-v in different lunar exploration mode (m/s)

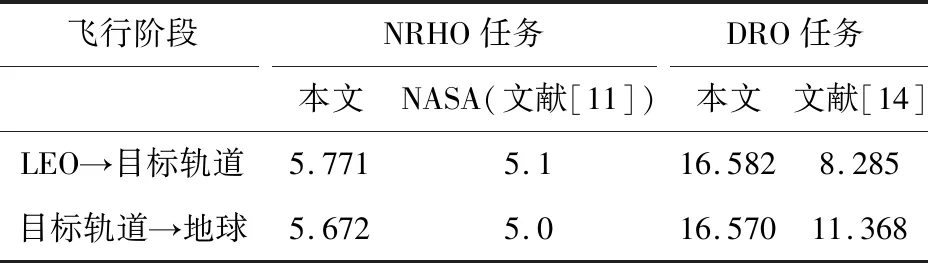
表2 不同探月模式的飞行时间Table 2 The associated flight time in different lunar exploration mode (天)

比较NRHO与DRO两种模式的往返转移任务，NRHO转移所需的速度增量较大，此类型转移可运用于短时间飞行任务。DRO转移虽然降低了任务的燃料消耗，但飞行时间显著增加。比较不同文献结果，NRHO转移时间改变量仅为1.343天，而借力点与入轨点机动增量减小63.803 m/s。基于本文方法的DRO往返适合于以燃料为主要指标要求的转移任务，通过数据比对进一步验证了所提设计策略的有效性。