矽卡岩分布的空间插值比较——以兴海县赛什塘矿区为例

徐睿泽

(中国地质大学(北京) 信息工程学院，北京100083)

地质钻探是矿产勘探和地质调查的直接手段，但经常面临缺乏全面完整的大数据支撑[1]，受地质钻孔成本及研究区地质环境等因素的影响，已有的钻孔点一般是离散不规则的，需要通过空间插值的方法利用有限的钻孔数据模拟连续的地质体曲线[2]，进而满足分析研究区岩石分布深度随空间变化的需求.因此，如何获取岩石的空间分布在理论和实际应用上都具有十分重要的意义.而空间插值是获取地理要素空间信息的常用方法，该方法能够将离散分布的钻孔点转换为连续分布的曲面数据.但受时空效应、模型算法和样本数据属性等因素的影响，各种模型的精度均存在差异[3]，“包插百量”的最优差之方法是不存在的[4].因此，需要针对数据属性和研究区的地理位置比较不同的空间插值方法，进而选出最优的插值模型.

利用钻孔数据进行插值重构工作，对明确矿区内矿体的赋存空间和找矿工作具有参考价值和实践意义.然而，针对兴海县赛什塘矿区，大量研究多集中于该地区的矿床地质特征[5-6]、矿床成因[7-8]和矿床富集规律[9]，有关该矿区内各岩石深度的空间分布及变化规律的研究却少有报道.因此本文基于赛什塘矿区已有的钻孔数据，以矽卡岩为研究对象，比较不同插值方法的预测误差及区域内的分布趋势，进而结合最优插值模型进行空间分布研究，旨在为相关部门及研究人员掌握赛什塘矿区内矽卡岩深度分布提供帮助，同时为该矿区内矿床矿体流体特征的深入研究和分析提供基础与保障.

1 研究区和数据源

1.1 研究区

赛什塘矿区的地理坐标是北纬35°18′00″，东经99°47′00″，地处鄂拉山地区的东南部，隶属于青海省兴海县.该矿区所处的地质环境十分复杂，内部以褶皱构造为主，断裂构造为辅，其西北向的构造控制着研究区内岩石的分布特点.矿区的总面积达3.435 km2,且矿区内矿种丰富，是整个青海省的重要矿带.

1.2 数据源

以青海省兴海县赛什塘矿区为研究区域，统计研究区1970～2009年内共计498个钻孔点，其中钻孔的经纬度和钻孔中包含的主要岩性数据均来源于全国重要地质钻孔数据库服务平台.同时，筛选出含有矽卡岩的钻孔点，并利用孔口高程与该岩性的深度做差来消除地形影响，从而获得矽卡岩分布的相对深度.

2 研究方法

主要借鉴易湘生[10]等人针对土壤厚度的空间插值研究方法和徐存东[11]等人针对地下水埋深的空间插值研究方法,同时参考了气象数据[12]、降水量数据[13-14]的空间插值研究方法，将地统计学的空间插值方法引用到本文针对矽卡岩深度的空间分布探究中.

2.1 探索性空间数据分析

探索性空间数据分析旨在探究数据是否具有空间相关性，是进行空间插值的前提.本文利用ArcGIS软件的地统计学分析模块进行矽卡岩深度的趋势分析和变异性分析，同时利用Geo Da软件进行钻孔点的空间自相关分析.

2.2 空间插值方法

克里金插值是以空间自相关性为基础，利用原始数据和半方差函数的结构性，对区域化变量的未知采样点进行无偏估计的插值方法，是地统计学的主要内容之一[10].为科学地筛选出相对最优模型，本研究首先在控制半方差函数为球状模型和插值方法的普通克里金插值条件下比较一阶与二阶多项式的优劣，进而比较三角函数、球面函数、指数函数、高斯函数四种半方差函数模型，最终通过比较普通克里金、泛克里金、简单克里金、指示克里金插值方法筛选出最为适合的相对最优模型.

2.3 模型检验方法

利用交叉验证法进行模型检验与比较，进而筛选出该研究区域中矽卡岩深度分布的相对最优模型.采用平均误差(ME)、平均标准误差(ASE)、标准化均方根误差(RMSSE)、标准化平均误差(MSE)、均方根误差(RMSE)对插值结果进行比较.其中，以下各插值结果作为较为良好的效果：ME绝对值接近0；ASE与RMSE较为接近；RMSSE接近于1；MSE较为接近0；RMSE越小其插值效果越理想.

3 研究结果

3.1 矽卡岩深度分布的探索性空间分析结果

将钻孔点数据进行Log变化后，偏度更接近于0,且数据的平均值与中位数更加接近，数据基本符合正态分布.研究区中部地区的采样点与邻域数值呈高高聚集，西北地区呈低低聚集，反应累积分布函数p≤0.05，初步判断数据符合空间自相关性.

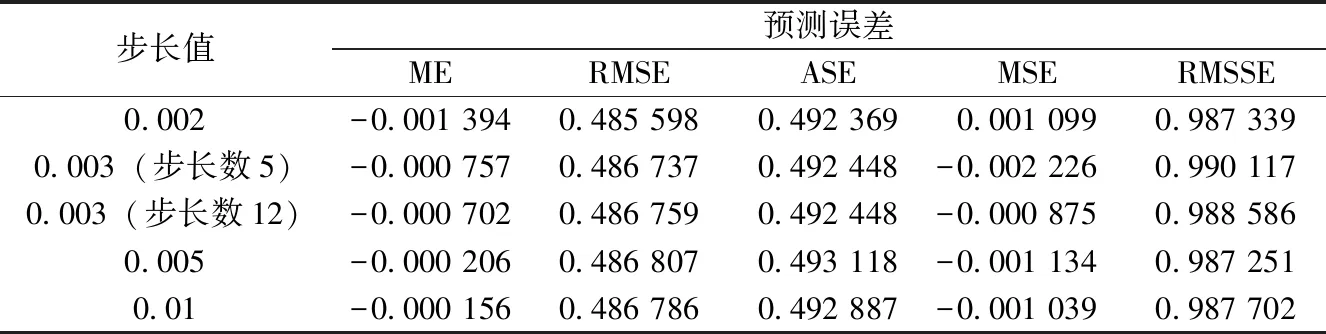
表1 不同步长值及步长数下的指示克里金插值的预测误差

按钻孔点的分布位置均匀地删除9个点，并对其进行克里金插值，将删除点前与删除点后的插值结果进行减法运算，发现删除点后的插值图与原图差别不大，因此认为选取的钻孔点符合平稳性假设.同时，在进行数据的差异性分析中，通过改变步长值和步长数，能够有效减小误差(表1，88页)，得到更加准确的插值结果.

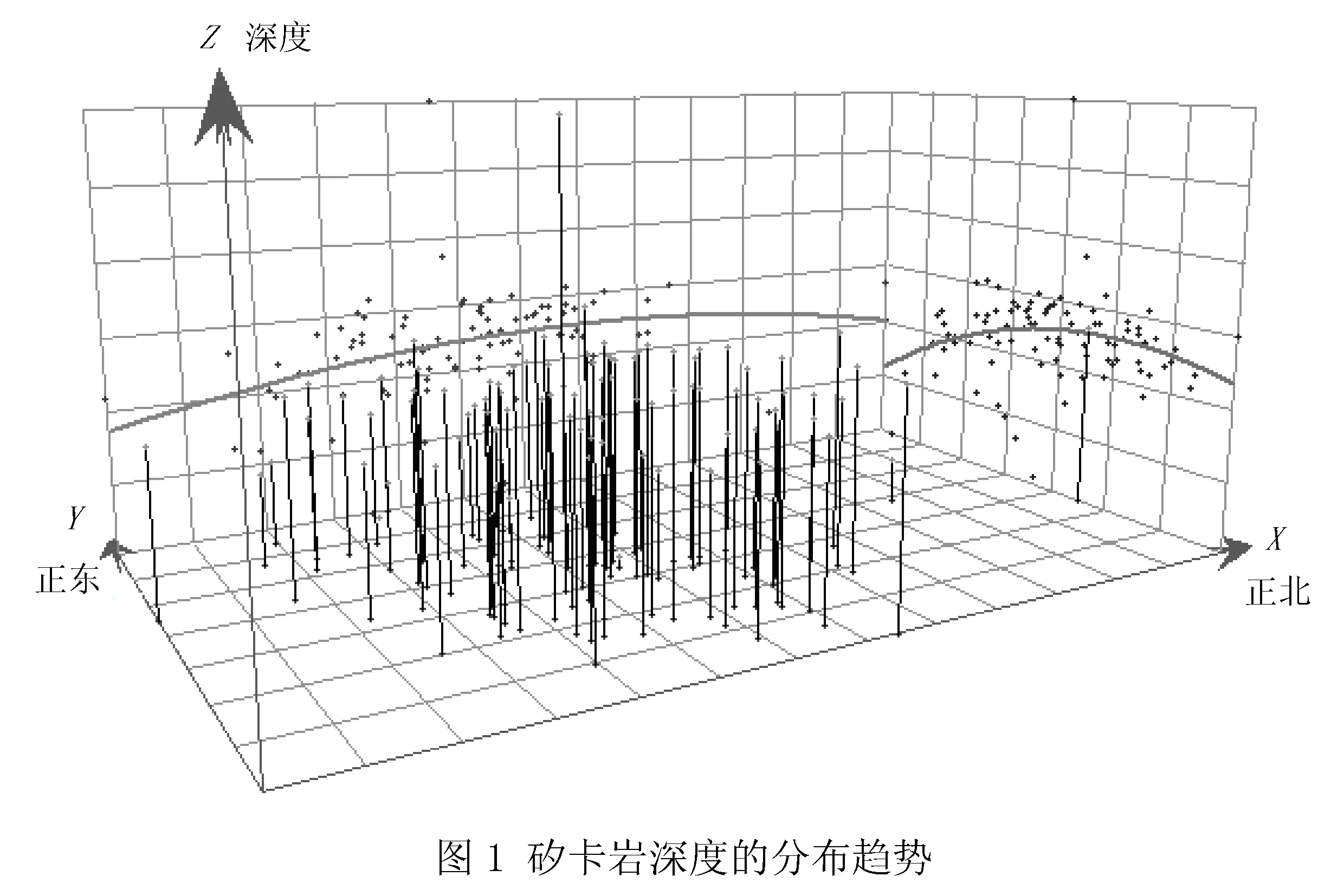
图1 中，Y轴表示正北方向，X轴表示正东方向，Z轴表示各个采样点矽卡岩深度的空间趋势图，XY轴平面上的竖直线代表每个采样点矽卡岩的深度及其所在的空间位置，两个竖直投影平面上的曲线分别对应南北和东西的趋势效应变化情况.结果表明，塞什塘矿区矽卡岩深度分布在两个方向上基本呈一阶或轻微的二阶多项式的变化趋势.在后续的研究中通过两种趋势效应的比较，可以更科学准确地进行趋势判断.

3.2 克里金插值的比较

3.2.1 趋势判断

在选用普通克里金插值的前提下，针对四种函数分别选用一阶多项式和二阶多项式的趋势效应，从而比较不同趋势效应的插值效果.由表2可以看出，二阶的ASE和RMSE的值更接近，且二阶趋势的RMSSE比一阶趋势稍大，误差值更接近1.由交叉验证的结果可以看出，二阶趋势的插值方法总体上比一阶插值方法理想.

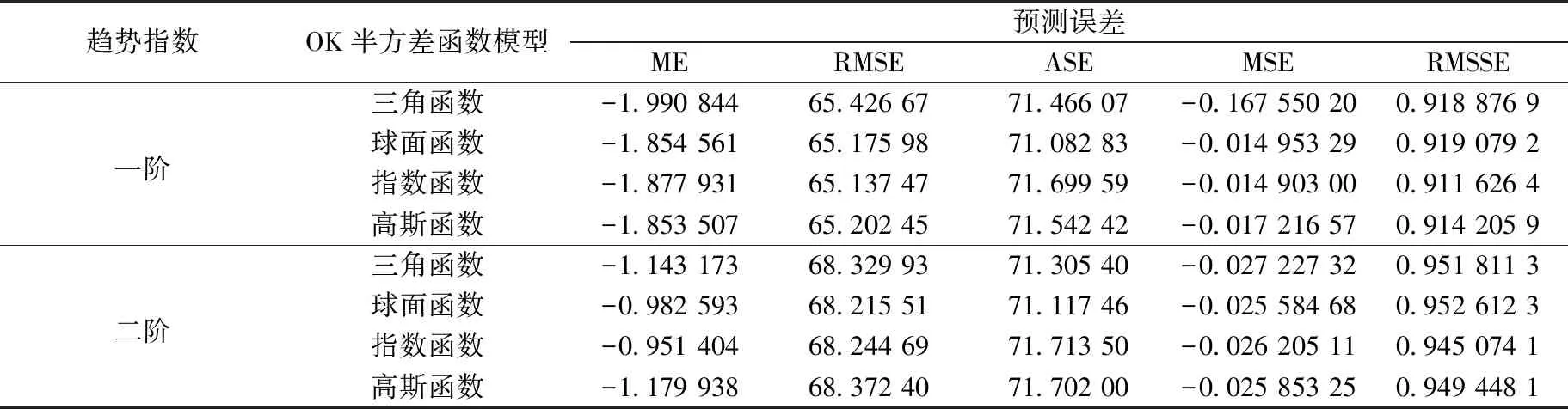
表2 普通克里金插值的预测误差

3.2.2 半方差函数比较

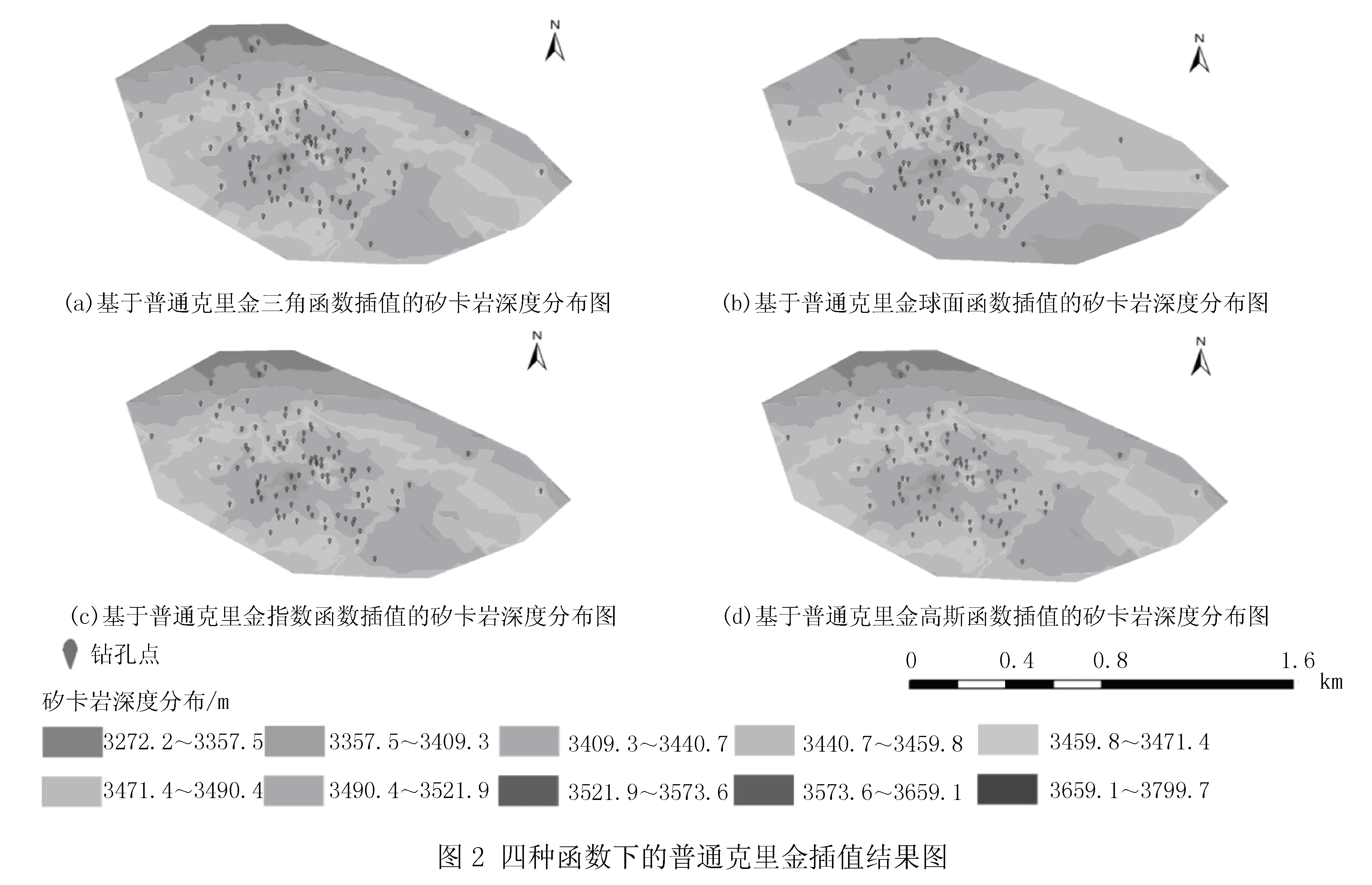
基于表2中二阶克里金插值预测误差比较分析发现，球面模型的RMSE值最小，MSE的绝对值最接近于0且RMSSE的值最接近于1，因此在ME误差相差不大的情况下，通过数据初步判断普通克里金球面模型的插值效果最好.同时通过图2(a)～(d)的对比，球面函数插值效果更平滑，更符合实际情况，而其他函数的插值效果会出现较明显的断层现象.

3.2.3 四种克里金插值结果

基于上述研究结果发现，球面模型是最适合本研究区的函数模型，因此本小节基于球面函数模型进行四种克里金插值的比较，分别从预测误差(表3，90页)和插值结果图(图3，90页)两方面判断最优模型.从预测误差方面看，泛克里金的预测误差远远大于其余三种插值方法，ME的绝对值甚至为其他插值方法的几倍，相比较而言，指示克里金的插值预测误差要远远小于其余三种插值方法.四种基于球面函数模型的克里金插值结果图，可以直观地反映插值效果.普通克里金插值方法有较多的数据特异点，存在“孤岛”现象，这与插值的意义相背；基于泛克里金的插值方法在赛什塘矿区东部出现了很多分层情况，其插值效果较差；根据简单克里金插值图基本判断不出矿区矽卡岩的分布规律，无法对分布情况进行判断；而指示克里金插值结果更平滑，效果相对更好.

表3 矽卡岩深度分布的地统计学内插方法预测误差

4 讨论

对于空间插值结果，没有绝对最优的插值方法，要根据具体的条件和实际情况，对不同的研究区选取最佳方法[15].为得到理想的插值效果，就要对采样点数据进行充分的分析及恰当的函数变换.在控制变量的前提下，反复实验比较，选出最佳的插值方法.克里金插值是以半变异函数为理论基础的一种线性无偏最优估计，对于具有空间相关性的矽卡岩深度数据，可以得到较为满意的插值结果.综合兴海县赛什塘矿区矽卡岩深度的插值分布效果及误差验证结果，基于球面函数模型的指示克里金插值为本研究的最优插值模型.普通克里金插值因光滑效应，对于局部不连续性的情况并不能很好地模拟研究区内矽卡岩的深度空间分布.而泛克里金假设数据中的趋势是能够用确定的多项式来拟合的，而本文矽卡岩深度数据的分布趋势并不明显，难以利用确定的多项式拟合，因此泛克里金的插值方法在本文中并未突出其优势.

5 结论

基于兴海县塞什塘矿区钻孔数据，综合比较四种空间插值方法对矽卡岩深度空间分布的预测误差和插值结果图，得出以下结论：

(1)矽卡岩深度数据呈正态分布且其空间自相关性较强；东西和南北方向矽卡岩深度数据均呈现一阶或轻微二阶分布趋势；方差变异分析中，步长数在5～12，步长值在0.002～0.01范围内，会得到相对最佳插值结果.

(2)基于球面模型的OK、IK、SK和UK，经过交叉验证进行误差预测，球面指示克里金插值效果更符合实际.

(3)基于插值结果，本矿区西北部矽卡岩深度分布最浅，中部和东南部矽卡岩深度分布相对最深.而由于东部地区钻孔点相对较少，出现轻微断层现象，可能与实际分布情况不相符.