基于时间序列ARIMA模型的高职高专院校生师比预测

于明星

(朝阳师范高等专科学校 信息工程系，辽宁朝阳122000)

0 引言

随着我国经济的迅速发展，高职高专阶段的生源数量显著提高，高校的招生数量也随之升高.高职高专教育已由稳定发展期过渡到新探索时期，学生数量的持续增加和毕业生质量的下滑受到社会的普遍关注.为了实现教育大众化、现代化、公平化，教育部颁布了系列文件[1],其中2004年印发的《普通高等学校基本办学条件指标》中就招生规模及招生条件等多项指标作出了规定，明确指出在校生人数与专任教师比率不应超过18∶1.生师比是反映高职高专院校办学质量的一项重要指标[2]，是高等教育大众化进程中质量建设的基础，是一流大学守望精英教育质量的传统，是高等教育大众化进程中大学质量改革的理性判断[3].高职高专院校在积极扩招的态势下，在校生数量急速增长，但专任教师数量增幅却跟不上节奏，严重影响了高职高专教育的教学质量.通常生师比比值与教学质量具有反比关系，文献[4]通过分析2003～2013年间全国普通高校生师比的数据发现，国家重点建设大学及985工程大学的生师比较低，并针对高校生师比现状，提出了一些改善生师比的对策.文献[5]利用遗传算法优化的BP神经网络模型对未来几年普通高校的生师比进行了预测.文献[6]利用数据平台建立了高职院校生师比状态函数，进而通过数据函数值来分析院校的办学质量及办学规模等.

目前，已有较多研究关注生师比这一指标，大多集中于本科院校的现状及对策上的分析，而对高职高专院校生师比指标的预测研究相对不足，这影响着我国高职高专教育的招生及可持续性的健康发展.本研究中通过分析教育部高职高专院校的生师比数据，结合自相关系数表和偏自相关系数表来判断初始数据的平稳性，分析出自回归分量阶数p和移动平均分量阶数q，进而确定相应的ARIMA(p,d,q)模型，通过该模型来预测未来几年高职高专院校生师比指标.

1 ARIMA数学模型

ARIMA(全称Auto Regressive Integrated Moving Average)模型，即自回归移动平均模型，由Box-Jenkins于20世纪70年代提出的是一种时间序列分析法[7]，其基本思路是对初始数据进行时间上的阶数平移而形成一个随机序列，用以描述这个随机序列的属性模型就是ARIMA模型.该模型可以利用时间序列的过去值去分析未来值，在预测农产品价格[8]、交通事故[9]、网络流量[10]和电气负荷[11]等多方面具有广泛的应用.ARIMA模型中有三个参量，分别为自回归分量阶数p、差分次数d和移动平均分量阶数q，通常用ARIMA(p,d,q)表示[7].

结合高职高专院校不同研究数据的特点，构建最优的ARIMA预测模型.定义研究数据观测值zt满足

zt=λ1zt-1+λ2zt-2+λ3zt-3+…+λpzt-p+vt

(1)

式中：λt—— 回归参数，其中i=1，2，…，p为滞后变量数；vt—— 白噪声过程.则线性数据观测值zt就是p阶自回归模型，表示为AR(p).

白噪声vt用滞后算子表示为

vt=Λ(L)zt=(1-λ1L-λ2L2-…-λpLp)zt

(2)

式中：Λ(L) —— 自回归算子.

自回归算子变式为

(3)

当特征方程满足Λ(L)=0时，AR模型在p阶平稳.

若研究数据观测值zt满足

zt=vt+θ1vt-1+θ2vt-2+θ3vt-3+…+θqvt-q

(4)

式中：θ1,θ2,…，θq—— 参数；vt-q——t-q时所对应的白噪声.研究数据观测值zt就是q阶移动平均模型，表示为MA(q).

式(3)变形为

zt=Θ(L)vt=(1+θ1L+θ2L2+…+θqLq)vt

(5)

式中：Θ(L)——移动平均算子.

移动平均算子特征方程为

Θ(L)=1+θ1L+θ2L2+…+θqLq=0

(6)

移动平均算子变式为

(7)

那么,研究数据观测值

(8)

式中：k1,k2,…，kq——常数.

当特征方程满足Θ(L)=0，MA模型在q阶可逆.

ARMA模型由AR模型和MA模型组合构成，表达式为

zt=λ1zt-1+λ2zt-2+λ3zt-3+…+λpzt-p+vt+θ1vt-1+θ2vt-2+θ3vt-3+…+θqvt-q

(9)

综合式(2)和式(5)，ARMA模型可变形为

Λ(L)zt=Θ(L)vt

(10)

若时间序列不具有平稳性，则需要对不平稳模型进行差分处理，那么此ARMA模型就是ARIMA模型.

为了分析数据的变化率情况，引入增比指标，其表达式为

(11)

式中：zi——第i年的数据；zi-1——第i-1年的数据.

其基本过程为：

(1)根据初始高职高专院校教育统计数据的自相关系数表和偏自相关系数表判定序列的平稳性，通常初始的数据为不平稳的时间序列.

自相关系数计算公式为

(12)

偏自相关系数计算公式为

(13)

(2)若初始的统计数据为非平稳的时间序列，且具有一定的变化趋势，则对该组数据进行一阶差分处理，如果一阶差分后的数据依然为非平稳的时间序列，则进行二阶差分处理，一般差分次数控制在2次之内.

(3)根据时间序列模型判定规则[7]，建立合理的时间序列模型.若偏自相关系数呈截尾性，自相关系数呈拖尾性，则移动平均分量阶数为0，自回归分量阶数为p；若偏自相关系数呈拖尾性，自相关系数呈截尾性，则移动平均分量阶数为q，自回归分量阶数为0；若偏自相关系数呈截尾性，自相关系数呈截尾性，则移动平均分量阶数为p，自回归分量阶数为q.

(4)利用步骤(3)确定的ARIMA(p,d,q)分析初始数据，得出预测结果.

ARIMA模型能够依据变量自身的变化规律，利用外推机制判断出研究对象的变化情况,通过处理预测目标的时间序列，获得事物随时间变化的演变特性及规律，从而预测事物未来的发展方向.ARIMA模型的基本适用条件是要求预测的数据满足平稳性特征，即个体值要围绕均值小幅波动，存在某些周期规律特性，且不存在明显的变化趋势(若出现明显变化趋势，则需要对预测数据进行差分处理).高职高专院校的在校生数量和专任教师数量随着年份的增加而不断变化，虽然在每个季节的数量都不尽一致，但却存在某种规律性，每一年周期内在校生数量和专任教师数量的波动趋势大致相似，具有连续性和周期性，故适用ARIMA模型进行预测.

2 高职高专院校现状分析

表1为高等教育院校规模变化表，数据来源于教育部网站公布的2009～2017年全国教育事业发展统计公报[12～20].由表1可知：高职高专院校数量比本科院校要多；本科院校数量从2009年开始逐年上升，高职高专院校数量从2009～2017年也稳步提升；2012年以前高职高专院校的增长幅度较大，2012年以后其增长幅度落后于本科院校，但自2017年开始，增长幅度再次超过本科院校.

表2为高等教育专任教师数量变化表，数据来源于教育部网站公布的2010～2017年全国教育事业发展统计公报[13～20].由表2可以发现:本科院校专任教师数量比高职高专院校专任教师数量多;本科院校专任教师数量从2010年开始逐年上升，高职高专院校数量从2010～2017年也稳步提升;2015年以前本科院校专任教师增比要大于高职高专院校，自2015年开始，高职高专院校专任教师增比幅度大于本科院校;就总体趋势来看，本科院校专任教师增比处于下滑趋势，高职高专院校专任教师增比处于稳步上升趋势.

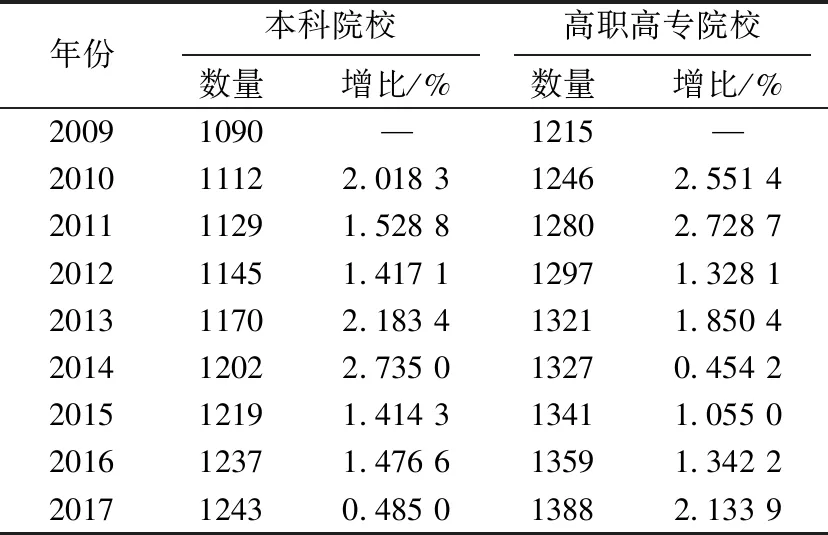
表 1 高等教育院校规模变化表

表3为高等教育在校生数量变化表，数据来源于教育部网站公布的2010～2017年全国教育事业发展统计公报[13～20].由表3可以看出:本科院校在校生数量比高职高专院校在校生数量多;本科院校在校生数量从2010年开始逐年上升，高职高专院校在校生数量从2010～2017年也稳步提升;在2013年以前，本科院校在校生增比要大于高职高专院校，自2014年以后，高职高专院校在校生增比幅度大于本科院校;就总体趋势来看，本科院校在校生增比处于下滑趋势，高职高专院校在校生增比呈上升趋势.表1～表3中出现的增比指标按式(11)计算.

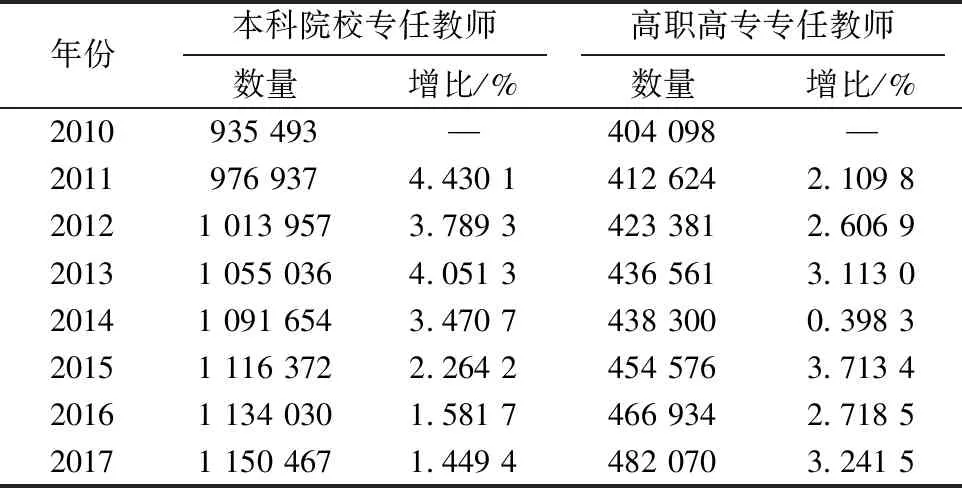
表 2 高等教育专任教师数量变化表

表 3 高等教育在校生数量变化表

3 ARIMA模型应用

本文从教育部2009～2017年度全国教育统计资料中获取了高职高专院校规模、专任教师数量、在校生数量的基本数据，这些数据真实且按时间顺序排列，具有时间序列特征，能够反映某类现象的统计指标，且存在时间性和周期性，故借助应用比较成熟的时间序列模型ARIMA进行研究.

表4为高职高专院校专任教师数量数据的相关系数分布表，其中ACV表示自相关系数值，PACV表示偏自相关系数值.若自相关系数值在标准差宽度范围内，则表明数据落入随机区间内部，为稳定的时间序列.初始分布的标准差宽度为0.39，一阶差分的标准差宽度为0.54.由表4得出，初始的ACV在滞后6阶时，自相关系数值在随机区间外部，需要对初始数据进行差分处理.一阶差分后的自相关系数和偏自相关系数若全部落入随机区间内部，经一阶差分后的数据为平稳时间序列，那么自回归分量阶数p为0，差分次数d为1，移动平均分量阶数q为0，那么选用的时间序列模型为ARIMA(0,1,0).

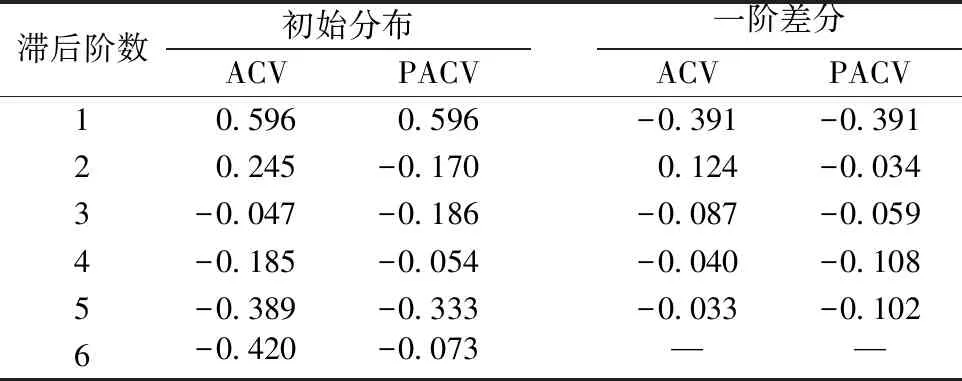
表 4 高职高专院校专任教师数量数据的相关系数分布表

表5为高职高专院校在校生数量数据的相关系数分布表.初始分布、一阶差分和二阶差分的标准差宽度分别为0.36、0.45和0.56.由表5可知:第1阶、第5阶和第6阶自相关系数值在随机区间外部，数据为不平稳的时间序列；第1阶偏自相关系数在随机区间的外部，从第2阶起全部落入随机区间内部，表现出截尾性，自回归分量阶数p为1.但是，已由自相关图判断出该数据为非平稳时间序列，需要进行平稳化处理.经一阶差分后，滞后第1阶和第4阶的自相关系数在随机区间外部，则移动平均分量阶数q为4，滞后第2阶及以后的偏自相关系数均落入随机区间内部，则差分次数d为1，自回归分量阶数p为1，那么选用的时间序列模型为ARIMA(1，1，4).考虑到收集样本数量较少，滞后阶数过多可能影响预测结果的准确度，本文将对一阶差分后的数据再次进行差分处理.二阶差分后，所有阶数的自相关系数和偏相关系数均落入随机区间内，呈拖尾性，经二阶差分后的数据为平稳时间序列，自回归分量阶数p为0，差分次数d为2，移动平均分量阶数q为0，则选用的时间序列模型为ARIMA(0,2,0).

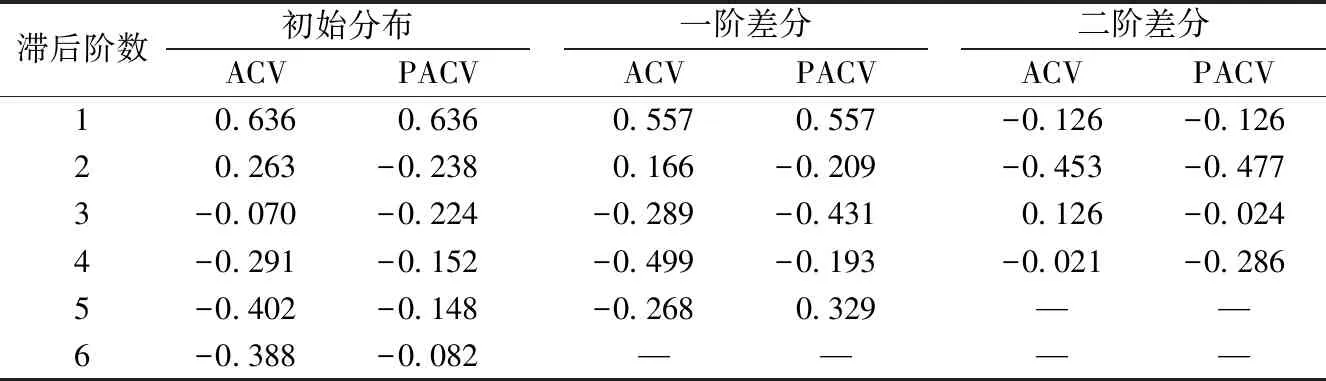
表 5 高职高专院校在校生数量数据的相关系数分布表

4 预测结果分析

通过ARIMA(0,1,0)模型对高职高专院校专任教师数量进行时序分析，其预测结果如表6所示，下限值指的是置信区间下限，上限值指的是置信区间上限.由表6可知，预测模型结果均在显著性水平0.05的置信区间内，预测结果具有较高的可信度.预测结果显示,2018年、2019年和2020年的专任教师数量分别为488 748人、499 613人和510 478人.从整体分布情况来看，高职高专院校专任教师数量在未来几年依然会保持持续增长的趋势.通过ARIMA(0,2,0)模型对高职高专院校在校生数量进行时序分析，其预测结果如表6所示，预测模型结果均在显著性水平0.05的置信区间内，具有较高的可信度。预测结果显示，2018年、2019年和2020年在校生数量分别为9 622 037人、9 997 531人和10 373 025人.从整体分布来看，高职高专院校在校生数量在未来几年依然保持持续增长态势.值得说明的是，为考察专任教师和在校生数量预测值的可信度，进行了相对误差百分比的评价计算，从数值上来看均不到5%，表明预测结果满足预测精度.

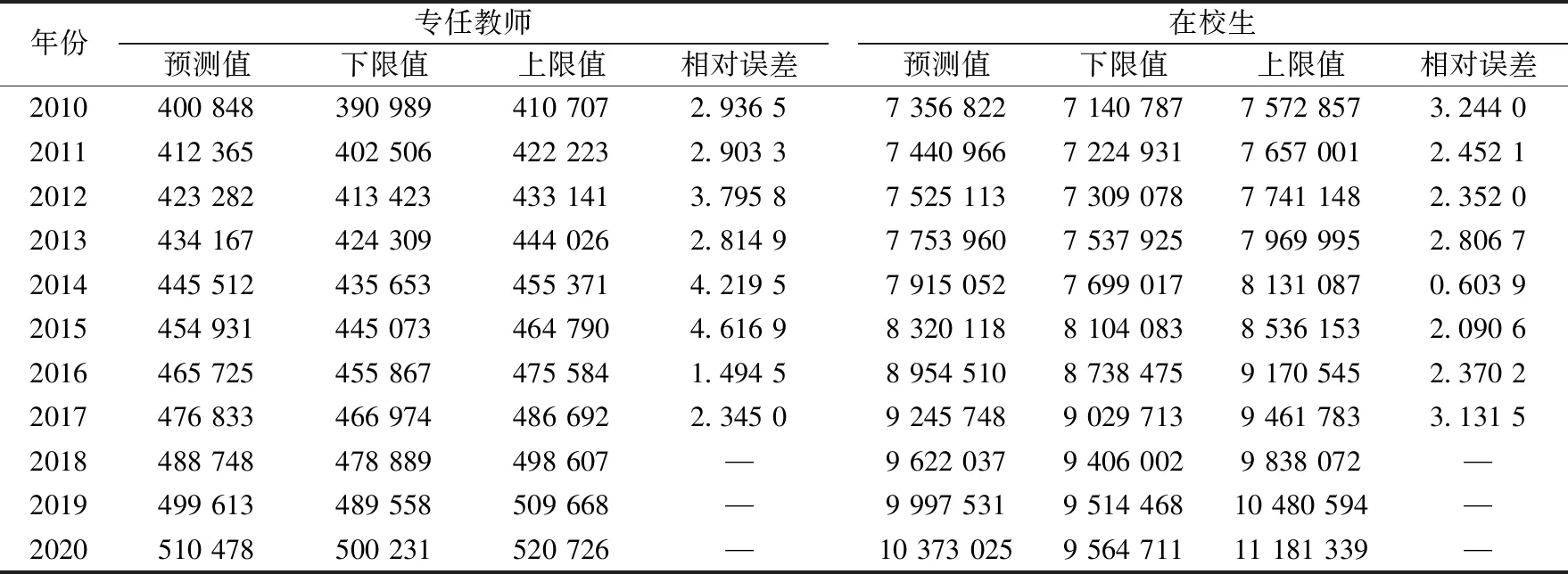
表 6 高职高专院校专任教师和在校生预测结果表

普通高校生师比定义为在校生数量与专任教师数量之比，教育部[2004]2号文件规定高等教育院校生师比的标准为18∶1，本文通过ARIMA模型预测结果计算了未来几年高职高专院校的生师比，如表7所示，给出了高等教育院校生师比预测值对照结果.由表7可以看出：本科院校的生师比一直低于16∶1；高职高专院校生师比在2013年以前基本上接近于18∶1，但从2014年开始增速加快，在2017年生师比达到19.18∶1.预测模型结果显示：2018年生师比为19.69∶1，2019年生师比为20.01∶1，2020年生师比位20.32∶1.生师比是判断世界顶尖大学的基本标准.泰晤士报上的大学排名，把生师比作为考量的重要指标.英国《独立报》编辑汤姆·门德尔松说过，“一所大学的学者越多，学生就会得到更多的关注，那么学生与教师的交流频率更多，他们在学习过程也会获得更有价值的内容”.创建一流的大学需要一流的师资力量，生师比数据就是一个需要考量的关键指标，教师越多，所营造的学术氛围和教学环境越好.英国《卫报》认为：生师比应考虑的是从事教学工作的教职员工，不包括从事少许教学工作的研究人员.生师比是反映大学教学质量的重要指标，良好的生师比是提升高职高专学生就业质量的基础保障.在未来的几年里，高职高专院校还需要保障良好的师资团队，控制生师比，为高职高专院校的可持续发展提供基本的保障.

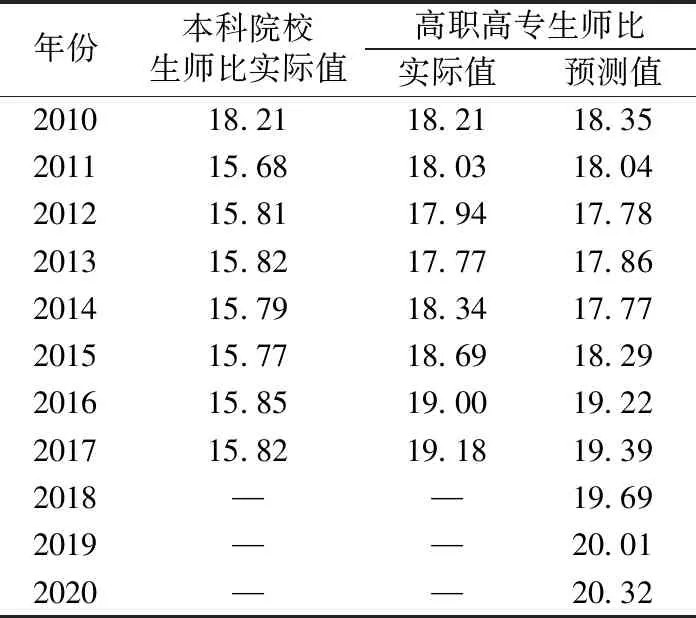
表 7 高等教育院校生师比预测值对照表

5 结论

高职高专院校的生师比指标关乎学校教育的质量，合格生师比指标为18∶1，限制招生生师比指标为22∶1.本文结合时间序列ARIMA模型对高职高专院校未来几年的生师比进行预测，得出结论如下：(1)就整体趋势而言，高职高专院校数量增幅较快，且其专任教师和在校生数量增比要高过于本科院校；(2)初始的高职高专院校教育统计数据是真实的，具有时间序列特征，但是多数为不稳定时间序列，需要进行一阶或二阶差分处理；(3)高职高专院校2018年生师比为19.69∶1，2019年生师比为20.01∶1，2020年生师比为20.32∶1.结果表明：未来几年内高职高专院校生师比呈上升趋势，将超过合格指标，为师资队伍建设及制定招生计划提供理论参考.