探寻解三角形中的最值问题,提升学生逻辑推理核心素养——从2019年一道解三角形题谈起

广东省佛山市顺德区均安中学(528329) 陈 锁

1 试题呈现

例1 (2019 全国Ⅲ卷理科数学第18 题) 已知ΔABC的内角A,B,C的对边分别为a,b,c,已知bsinA.

(1)求B;

(2)若ΔABC为锐角三角形,且c=1,求ΔABC面积的取值范围.

2 解法探究

本题第(1)问简单,通过正弦定理的边角互化即可解决.第(2)问思路也很清晰,正弦定理和余弦定理均可,但是问题是用哪个较为合适呢?从表面看,我们用余弦定理直观明了,得到方程a2－a+1－b2=0.从解析几何的角度来说,这是一个焦点在轴上,对称中心为图像范围在第一象限的部分双曲线.从函数的角度来说,这是一个关于a,b的函数三角形面积所以需要通过三边关系来确定的取值范围,从而求出面积的最值.由于正弦定理与余弦定理的等价性,我们也可以用正弦定理来解决此问题.由于由正弦定理得三角形面积再通过角的关系找出C的取值范围,从而求出面积的最值.

解法一(1)(过程略)

(2)由余弦定理b2=a2+c2－2accosB可得

由于ΔABC为锐角三角形,所以即

同理:

拓展延伸当三角形给定一个角度与其一邻边,如果我们从余弦定理入手的话,其实是研究一个二元二次方程的另外两边的变量关系.由于另外两边是一个函数关系式,当求其面积或者边长的取值范围的时候,可以利用导数研究函数的性质并求其范围.该题也可以变式为求三角形的边长关系.例如该三角形周长当a＞0 时,所以周长l在为增函数,所以周长l取值范围为也可以解决更一般的问题,比如的取值范围等.

解法二(1)(过程略)

(2)由正弦定理

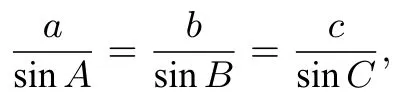
可得

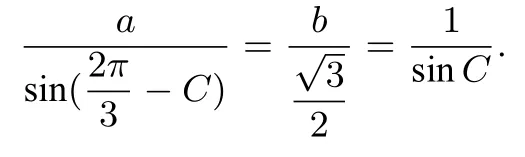
所以有

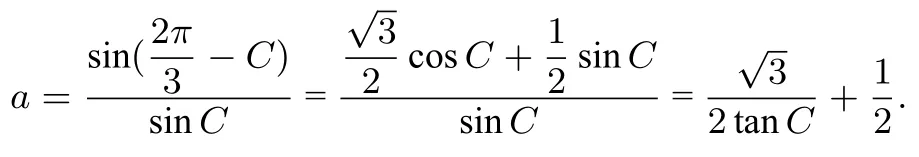
由于ΔABC为锐角三角形且则

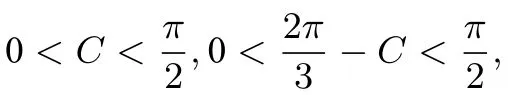
拓展延伸当三角形给定一个角度与其一邻边,如果我们从正弦定理入手的话,其实是研究一个分式型三角函数.当求面积或边长的取值范围的时候,我们可以从分式型三角函数的特点出发,利用导数求出取值范围,也可以利用两点的斜率公式求取值范围.例如该三角形的周长

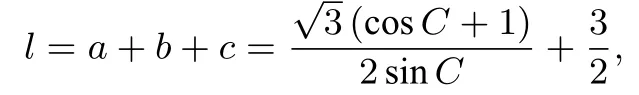
3 问题拓展

对于解三角形的最值问题,我们通过未知条件的变化,大体可以归结为三类:①已知一个角和其一条邻边的问题,②已知一个角和其对边的问题,③已知两条边的问题.从2007年的新高考以来,我们发现第一类问题在近两年有出现,分别是2018年江苏卷和2019年全国Ⅲ卷.第二类问题历年高考出现的频率较多,很多学生只是停留在用基本不等式求其最值,从正弦定理与余弦定理方面来探讨的较少.第三类问题全国卷暂时没有出现过,但值得去探讨.下面我们通过两个例题来探讨后面两种情况的最值问题.

例2已知a,b,c分别为锐角ΔABC的三个内角A,B,C的对边,a=2,且(2+b)(sinA－sinB)=(c－b)sinC,求ΔABC的周长l和面积SΔABC的取值范围.

试题分析本题化简后出现了2 sinA,bsinB,csinC,我们考虑可以用正弦定理把其转化为a2,b2,c2,然后用余弦定理得到又由于a=2,我们利用余弦定理得到二元二次方程b2+c2－bc=4.从解析几何的角度来看,这是一个焦点在直线c=b,对称中心在(0,0),图像范围在第一象限的部分椭圆;从函数的角度来说,这是一个关于b,c的函数而面积与周长均为关于b的函数.由于正弦定理与余弦定理的等价性,利用正弦定理得得到面积与周长均为关于C的函数.

解法一由已知条件及正弦定理得(a+b)(a－b)=(c－b)c,即b2+c2－a2=bc.又因为所以又因为b2+c2－bc－4=0,所以周长得,当l′=0 时,b=2,当b ∈(0,2),l′＞0,l为增函数;当l为减函数所以b=2 时,周长的最大值l=6.

又因为 ΔABC为锐角三角形,所以即所以

解法二同上由正弦定理得得到

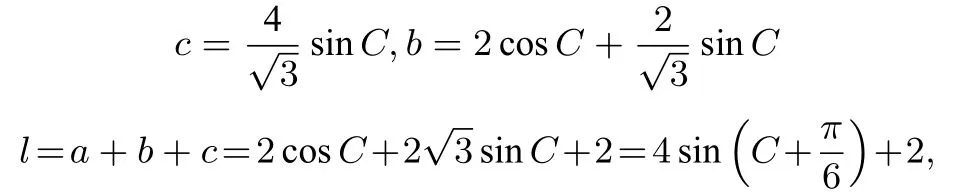
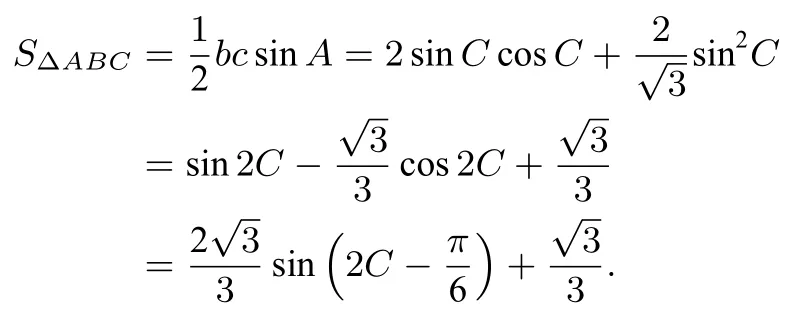
拓展延伸本题从正弦定理和余弦定理出发得到的函数类型是不一样的.如果该三角形有限定条件,则从余弦定理出发的等式需要从边的角度找到其限定范围,从正弦定理出发的等式需要从角的角度找到其范围.这两种方法均能解决一般的问题.比如2011年全国卷第16 题“ΔABC中,则AB+2BC的最大值为____”.如果从等式b2+c2=bc+4 的结构来看,利用基本不等b2+c2≥2bc求面积和周长的最值无疑是非常简洁的.因为4+bc=b2+c2≥2bc,所以bc≤4,等号成立时,b=c=2.SΔABC=所以当b=c=2时,面积的最大值

又因为(b+c)2－4=3bc≤所以b+c≤4,等号成立时,b=c=2.所以当b=c=2 时,周长的最大值l=6.但求锐角三角形的面积和周长的范围时,该方法就有所欠缺了,更不要说求AB+2BC取值范围了.

例3已知a,b,c分别为锐角ΔABC的三个内角A,B,C的对边,a=2,b=1,求ΔABC的周长l和面积SΔABC的取值范围.

试题分析利用余弦定理得到一个关于c的函数从而可以得到关于面积与周长的函数关系式.从正弦定理出发,我们能得到A,B,C的关系式,从而得到关于面积与周长的关系式.

解析由余弦定理得

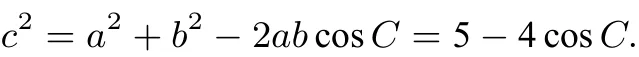
又因为ΔABC为锐角三角形,所以即即所

解法二由正弦定理得所以sinA=2 sinB,

又因为ΔABC为锐角三角形,所以 又所以所以又因为

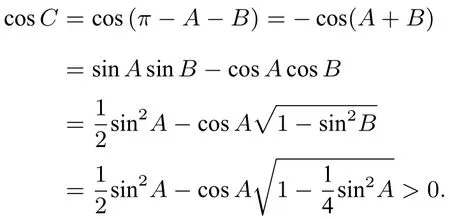
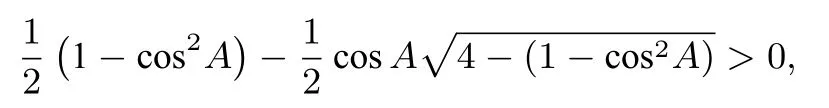
所以有

又因为

显然l是关于cosA的增函数.所以关于单调递增.所以

拓展延伸本题显然从余弦定理出发,从边的角度去寻找角度的范围要简洁得多;由于三个角度没有确定,如果从角A,B,C的关系去寻找角度范围要复杂得多.当然我们也可以从边角关系联立寻找角度范围也很简洁.由已知得即3＜c2＜5,即又因为得所以

4 方法总结

对于解三角形问题的最值问题,一般是通过对正弦定理与余弦定理为桥梁,通过知二求二的问题形式呈现,这类问题基本上都可以从函数的角度来考虑求解.如果题目限定了条件,比如三角形为锐角三角形,我们可以从边和角的关系分别去确定角度的取值范围,从而得到最值的范围.