人教社A版数学的一道B组习题之来龙去脉

安徽省安庆市第二中学东区(246003) 汪学思

命题已知0＜x＜1,0＜y＜1,求证:

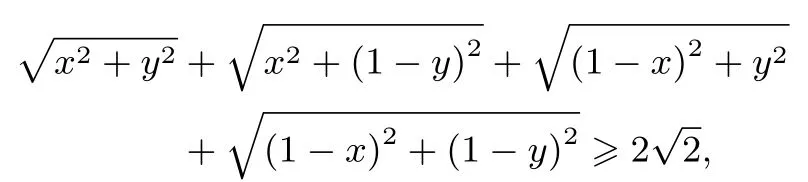
并求使等式成立的条件.该题是人教社A 版数学必修2 第三章习题3.3 的B 组第8 题[1].

本题来源于一道竞赛题:“已知a、b是小于1 的正数,求证

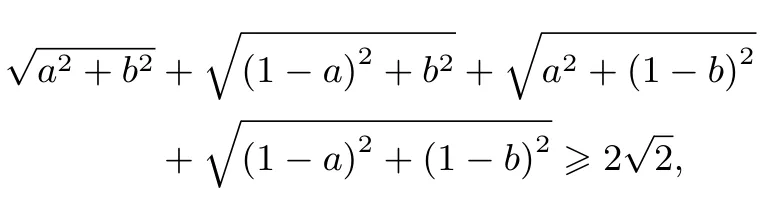
该命题我们很容易从不等式左边的结构上看出形似两点间的距离公式,令点P(x,y)、O(0,0)、A(1,0)、B(1,1)、C(0,1),利用两点间的距离公式,则将不等式的左边转化为与正方形顶点有关的线段和问题;即为正方形ABCO内部一点P到顶点A,B,C,O的距离和.如图1,得原题左边=|PO|+|PB|+|PA|+|PC|≥|OB|+|AC|=当且仅当P点位于线段OB与AC的交点时取等号,此时

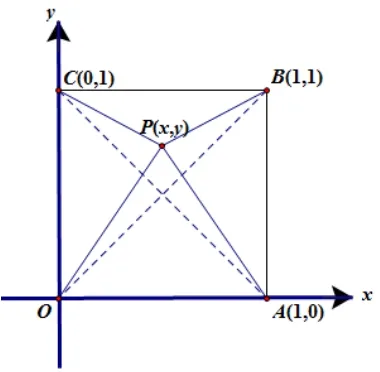
图1

而此时P点也正是四边形的费马点:数学上到四边形四个顶点距离之和最小的点为四边形的费马点.它是这样确定的:

(1)在凸四边形ABCD中,费马点为两对角线AC、BD交点P;

(2)在凹四边形ABCD中,费马点为凹顶点D(P).[3]

本题在这里既考查了两点距离公式,又让同学领悟到数形结合与转化的数学思想方法,既考查了距离的极值问题,又可以结合著名的费马点问题进行数学史的教育,激发学生在这方面的兴趣,可谓一题多得.

我们如果对该题的证明过程及几何意义进行琢磨和推敲,就不难发现这样的一个事实:

推论1在正方形的内接四边形(指四边形顶点分别在正方形的四条边上)中,凡是各边与正方形对角线分别垂直的四边形周长都相等且最小,等于两倍的正方形对角线长;反之亦成立.

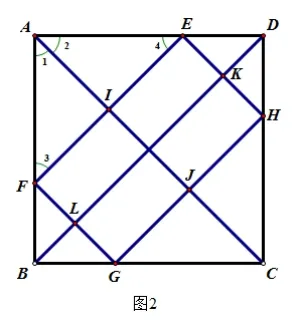
这个推论的证明如下:如图2,∵四边形EFGH各边分别与正方形ABCD的对角线AC、BD垂直,∴四边形EFGH为矩形.

设该矩形与对角线分别交于I、J、K、L,则EH=FG=IJ.

∵∠1=∠2=∠3=∠4=45°,∴EF=2AI.同理HG=2CJ;

∴四边形EFGH的周长=2AI+2IJ+2JC=2AC.

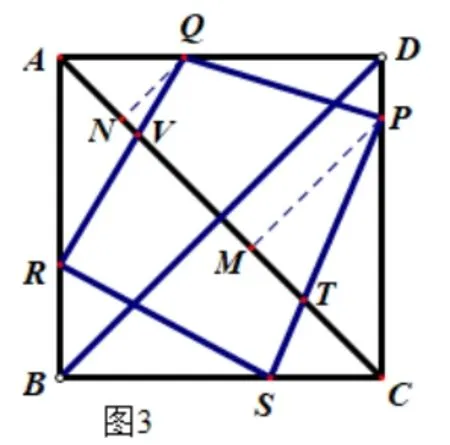
再设正方形ABCD另有一内接四边形PQRS,但PQ不垂直BD,如图3.

从P、Q分别向AC作垂线,垂足为M、N,则PQ＞MN.

设PS、QR分别交AC于T、V,则有PT≥PM=MC,QV≥QN=AN,

∴TP+PQ+QV＞MC+MN+AN=AC,同理可证TS+SR+RV＞AC;

∴四边形PQRS的周长＞2AC.

很明显,当正方形的内接四边形周长等于两倍的正方形对角线长时,其对边必与其中一条正方形对角线垂直,而另一组对边与该对角线平行.

综上所述,推论1 证毕.

该推论如果“翻译”成代数式,就可以得到一组系列不等式:

推论2若a、b、c、d为四个任意的非负数,且皆不大于另一任意正数L,则有:

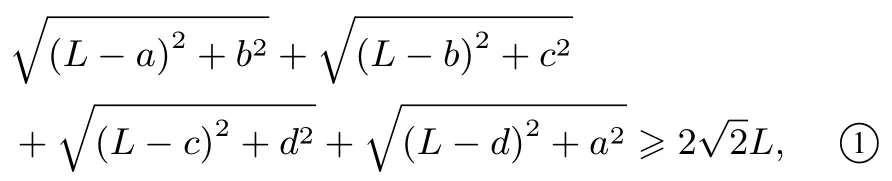
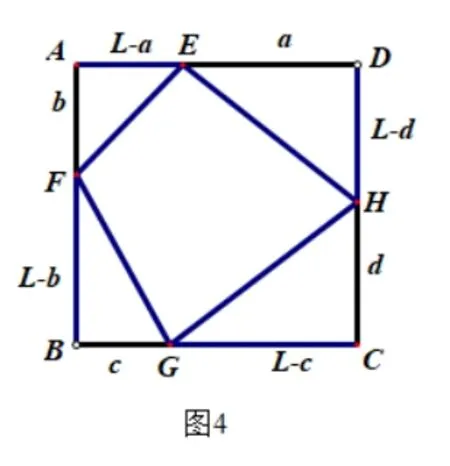
当且仅当b=d=L－a=L－c时,等号成立(参见图4);

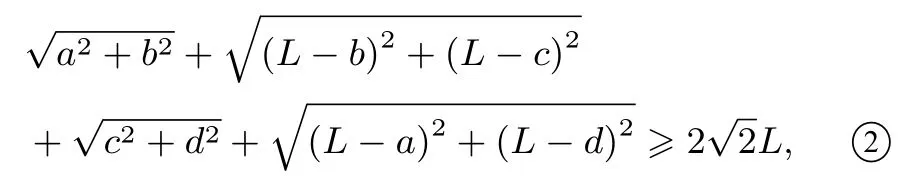
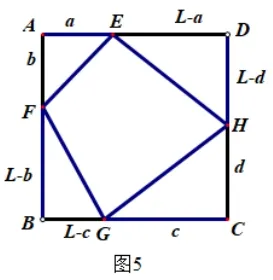
当且仅当a=b=c=d时,等号成立(参见图5);

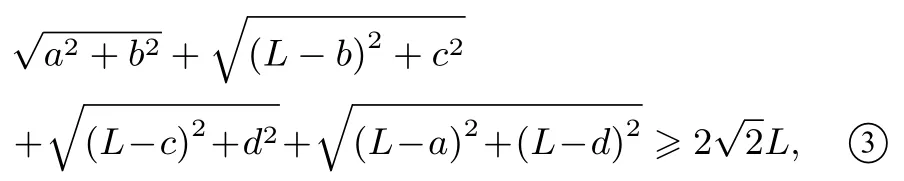
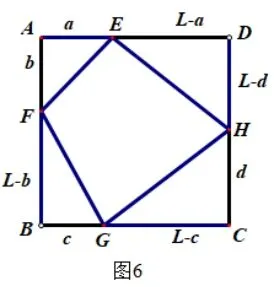
当且仅当a=b=L－c=d时,等号成立(参见图6);

······

由于推论1 中的内接四边行把正方形各边分成的各部分线段字母的设法不同(参见图4―图6,正方形边长为L),可造成推论2 中共有A12·A12·A12·A12=16 种不同形式的不等式.这16 个不同形式的不等式可以互化,如①式中的L－a与a、L－c与c互换,即可得②式.

可以看出,本文开头的命题,只不过是属于推论2中③式里的c=a、d=L－b且L=1 的这种情形而已.

我们若在推论2中令a=Lsin2α、b=Lsin2β、c=Lsin2γ、d=Lsin2δ,就不难得到用三角函数的形式表示推论2 相应各条的又一推论:

推论3对于任意角α、β、γ、δ,有下面一系列的关系式(共16 个)

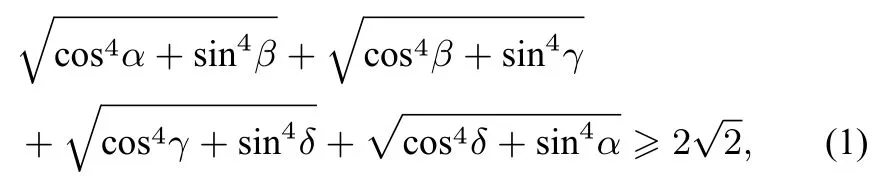
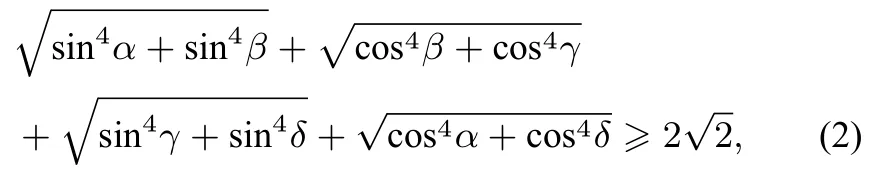
当且仅当α=kπ±β=lπ±γ=mπ±δ(k、l、m ∈Z)时,等号成立;

······
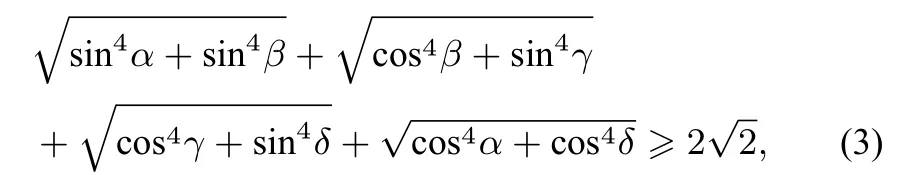