立足能力考查 凸显素养导向

山东省费县教育和体育局(273400) 吴士友

1 试题呈现

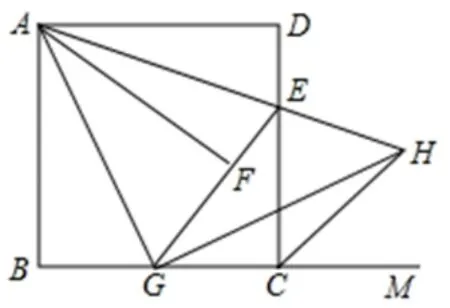
图1

(2019年临沂中考数学第25 题) 如图1,在正方形ABCD中,E是DC边上一点(与D,C不重合)连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于点G,连接AG,作GH ⊥AG,与AE的延长线交于点H,连接CH,显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察请逐一找出图中其他的角平分线(仅限小于180°的角的平分线),并说明理由.

2 核心素养视角下的特色解读

2.1 低起点宽入口体现面向全体

《义务教育课程标准(2011年版)》(以下简称《课标》)在“课程基本理念”中指出,数学课程应致力于实现义务教育阶段的培养目标,要面向全体学生,适应学生个性发展的需要,使得:人人都能获得良好的数学教育,不同的人在数学上得到不同的发展[1].试题中让考生寻找的角平分线共有四条:①AG是∠BAF的平分线;②GA是∠BGF的平分线;③CH是∠DCN的平分线;④GH是∠EGM的平分线.通过对题干内容的阅读理解和思考,大多数考生能较容易的找出角平分线AG和GA,并能很快写出AG、GA是角平分线的逻辑推理过程,找出并证明GH、CH是角平分线的台阶逐渐升高,难度逐步增大.从整体看,找出四条角平分线并一一证明,问题设置起点低,入口宽,有梯度,区分度好,它既能考查出学习水平一般的学生所具备的基本能力,又能考查出优秀学生的思维品质与综合素养,充分体现了题目面向全体的课程理念.120155 名考生的答题得分情况也吻合了这一设计理念,本题共11 分,其中有86938 名考生得分,约占72%,有58684 名考生得4 分以上(含4 分),约占49%,有3169 名考生得9 分以上(含9 分),约占2.6%.

2.2 立足能力考查培养创新意识

《课标》)在“课程内容”中指出,创新意识的培养是现代数学教育的基本任务,应体现在数学教与学的过程之中.学生自己发现和提出问题是创新的基础;独立思考、学会思考是创新的核心;归纳概括得到猜想和规律,并加以验证,是创新的重要方法.创新意识的培养应该从义务教育阶段做起,贯穿数学教育的始终[2].试题设问中未说有几条角平分线,考生需要经历观察、测量、探究、猜想等系列思维活动逐一找出角平分线,然后通过推理论证验证猜想,在逐一寻找和证明的过程中,充分考查了学生发现问题、提出问题、分析问题和解决问题的能力,逻辑推理论证的能力,较好的培养了学生的创新意识.

2.3 解题方法多样凸显素养导向

试题一方面考查了考生对角平分线的性质与判断、等腰三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质、轴对称的性质、正方形的性质等核心知识点的掌握与应用,另一方面考查考生的识图、作图能力;逻辑推理能力;运用数学活动经验综合解决问题的能力.证明GH是∠EGM的平分线是本题的难点,但题目设计思路开阔,解题方法多样,为不同思维层次的学生搭建了不同的平台,考生解答呈现百花齐放的局面,充分凸显了素养导向.下面重点展示证明GH是∠EGM平分线的部分证法,以供读者参考.

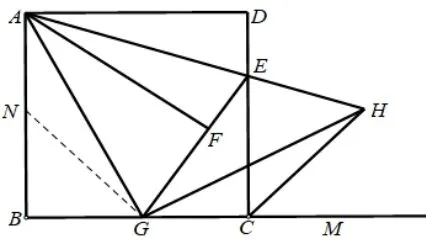
图2

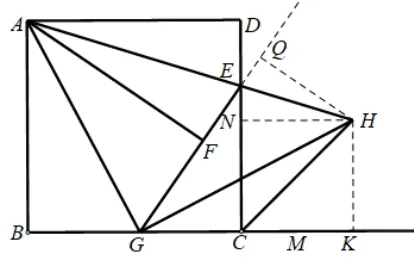
图3

做法一:如图2在AB上取点N,使BN=BG,连接NG.

证法1:易证△AGN～=△GHC,∠ANG=135°.

所以∠GCH=∠ANG=135°.∠HCM=45°=∠HCD.所以CH平分∠DCM.

做法二:如图3,过点H作GE延长线的垂线,垂足为点Q,作HN垂直CD于点N,HK垂直CM于点K.

证法2:易证∠QEH=∠NEH.HQ=HN.由CH是∠DCN的平分线(已证).知HN=HK,则HK=HN.CH平分∠DCM.

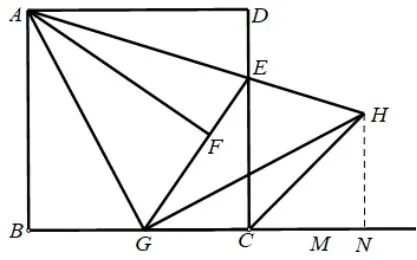
图4

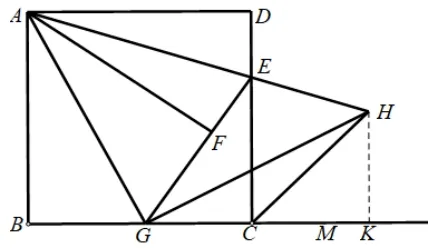
图5

做法三:如图4,过点H作HN ⊥CM,垂足为点N.

证法3:易证∠ABG～=△GNH(AAS).所以BG=NH,AB=GN,∠B=∠HNG=90°.则BC=GN.BG=CN.BC=GN.NH=CN.△HCN是等腰直角三角形.∠HCN=45°.∠HCN=∠DCM=45°.CH平分∠DCM.

证法4:如图5,截取GK=BC,连接HK.易证△ABG～=△GKH.所以BG=HK,∠GKH=∠ABG=90°.由做法知CK=BG,所以CK=HK.△CHK是等腰直角三角形.∠HCK=∠KHC=45°.CH平分∠DCM.

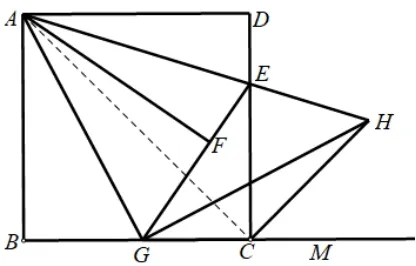
图6

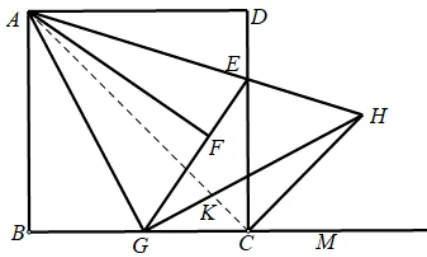
图7

做法五:如图6,连接AC.

证法5:易证∠AHG=45°.所以∠AHG=∠ACG=45°.A、G、C、H四点共圆.∠ACH=∠AGH=90°.∠HCM=180°－∠ACB－∠ACH=45°.CH平 分∠DCM.

证法6:如图6易证△AGH是等腰直角三角形.所以∠HAG=45°,因为△ABC是等腰直角三角形.∠BAC=45°,∠HAG－∠CAG=∠BAC－∠CAG.∠HAC=∠GAB.△ABG～△ACH.∠ACH=90°.∠ACB+∠HCM=90°.∠HAM=45°.CH平分∠DCM.

证法7:如图6,易证△AGH是等腰直角三角形.所以∠AHG=45°.因为△ADC是等腰直角三角形,∠ACD=45°.∠AHG=∠ACD.易证△EAC～△EGH.所以因为∠AEG=∠CEH.所以△EAG～△ECH.∠ECH=∠EAG=45°.CH平分∠DCM.

做法六:如图7,连接AC交GH于点K.

证法8:易证∠AHG=45°.因为∠ACB=45°.所以∠AHG=∠ACB.因为∠AKH=∠GKC.所以△AHK～△GCK.

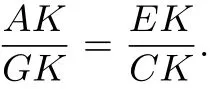
又因为∠AKG=∠HKC.所以△AKG～△HKC.∠ACH=∠AGH=90°.∠HCM=180°－∠ACB－∠ACH=45°.所以CH平分∠DCM.

做法七:如图8,截取GM=GE,连接HM,作HK垂直CD于点K,HN垂直BM于点N,

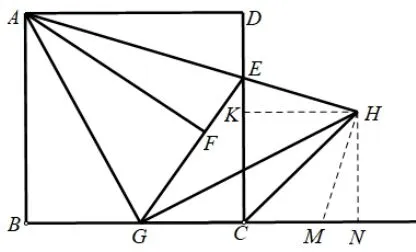
图8

证法9:易证△GEH～=△GMH.所以∠GHM=∠GHE=45°,HE=HM因为∠EHK+∠KHM=∠NHM+∠KHM=90°所 以∠EHK=∠NHMRt△EHK～=Rt△MHN,HK=HN,CH平分∠DCM.

3 教学导向分析

3.1 真正回归教材减轻学生负担

教材是《课程标准》的载体,是课程目标和课程内容的具体化,也是考试最公平化的素材,以教材中的问题为背景进行改编,创造性的开发利用教材资源,已成各地中考命题的主要方向.本题目是根据人教版八年级下册69页14 题改编,试题立足于教材而不拘泥于教材,命题意图清晰,既突出基础性,又体现选拔性,启示我们教师:“题海战术”练不出高分,以练代教,以练代学、以练代思的教学方式不可取,提高成绩的根本出路是要认真研究教材,创造性的使用教材,回归教学本源,减轻学生负担.

3.2 注重模型积累发展核心素养

“数学建模”是2017年新版高中课标所要求的数学学科素养之一,是学生应具备的关键能力.立足基本模型是解决图形问题的一个基本方法,在图形课学习过程中,要让学生充分认识和理解基本模型的本质,并不断积累模型.在解决具体问题时,善于调用和挖掘一些基本模型,有时需要添加辅助线构造出相关的基本模型,再利用其性质获取相应的结论,达到解决问题的目的.如本题中的证法一、证法三、证法四和证法九是添加辅助线构造全等形;证法六、证法七和证法八是添加辅助线构造相似形;证法五是添加辅助线构造四点共圆;证法二是添加辅助线构造角平分线模型.本题证法思路的探索都立足于常见的基本模型(全等形、相似形、辅助圆、角平分线).学生在观察、分析、构造和利用模型的过程中,提升了学科核心素养.

3.3 重视基础教学关注过程发展

重视新课教学,回归基础.新课紧紧围绕四个“点”下功夫:在情境中设置兴趣点,帮助基础较薄弱的学生建立数学学习的自信心,培养数学学习兴趣;在活动中抓住关键点,进入数学思考境地;提出质疑点,引领学生发现问题,提出问题;形成生成点,让学生经历数学基础知识形成过程,并掌握运用法则、公理、定理进行熟练运算、推理的基本技能,真正把基础知识和基本技能落实到位,而不能让基础知识和技能的学习走过场,死记硬背,导致缺乏对数学概念的真正理解.

重视思想方法引导,提高思维水平.数学思想方法的掌握是十分重要的,但思想方法的运用不是一蹴而就的,它不像知识点那样可以去直接传授,而应该是针对不同的数学学习内容、不同的情境给予不同方法的引导,从而提高学生的思维水平.如就合情推理、演绎推理的熟练应用;文字语言、符号语言、图形语言的熟练转化;类比与归纳、抽象与概括等思想方法的运用;都需要在逻辑推理教学中适时、适当、适度的引导和培养.