基于拓扑优化建立拉压杆模型的索塔锚固区环向预应力配束研究

罗芳

(湖南省湘西公路桥梁建设有限公司，湖南 吉首 416000)

斜拉桥索塔锚固区局部尺寸突变区域为典型D区，目前国内外尚无对D区预应力配筋设计的成熟方法，现有规范和设计方法建立在平截面假定的基础上，主要适用于B区，对于D区的受力分析则较粗略。常采用的索塔锚固区预应力配筋方法为根据经验对索塔环向预应力进行初步设计，结合有限元计算结果对预应力束进行适当调整。该方法存在耗时长、精度差、步骤繁琐及难以快速得到最优方案的缺陷。为解决上述问题，刘钊等通过索塔节段模型试验对润扬大桥北汊斜拉桥进行研究，验证了配束设计效果；沈璐等对索塔U形预应力束进行有限元仿真及足尺模型试验，对预应力束布置形式进行了探究；Schlaich J.提出了拉压杆模型理论、D区分析原则，该理论对简单几何结构具有很好的适用性，但对于索塔锚固区则很难找出准确的三维适用拉压杆模型。随着计算机技术的发展，通过拓扑优化建立拉压杆模型得以实现。在各类拓扑优化方法中，进化渐进优化法应用最广泛。该文以某特大斜拉桥为例，对锚固区索塔建立二维、三维模型进行拓扑优化，根据拓扑优化结果建立拉压杆模型，通过拉压杆模型指导预应力配束设计。

1 工程背景

某三跨连续半漂浮体系预应力砼斜拉桥，跨径布置为195 m+480 m+195 m，桥面标准宽度42 m，人行道净宽2 m，拉索区净宽1 m，非机动车道净宽2.5 m，边跨受立交闸道接入影响而加宽，索塔采用砼锚固齿块锚固斜拉索。主桥立面及索塔锚固区构造分别见图1、图2。

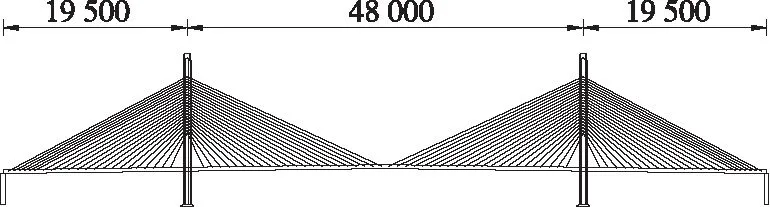
图1 桥型布置示意图(单位：cm)

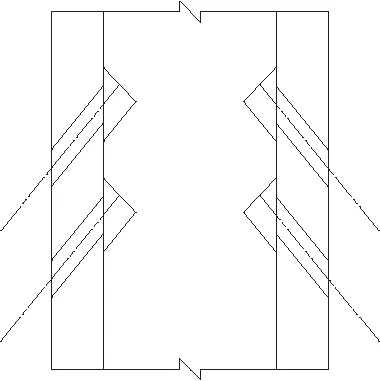
图2 锚固区构造示意图

2 拓扑优化分析

2.1 有限元模型建立

以索塔锚固区索力最大节段为控制节段，采用有限元软件Abaqus建立索塔横截面壳单元模型[见图3(a)]，将拉索水平分力荷载施加于齿块后进行计算，以计算所得应力结果作为拓扑优化分析的基础。根据设计文件，最大索力P=6 014.34 kN，对应拉索切线竖直倾角β=42.876°，水平分力PH=Psinβ=4 092.2 kN，将其作用于齿块上，得到第一主应力迹线[见图3(b)]。

图3 壳单元模型建立与计算结果

2.2 拓扑优化

拓扑优化是指通过在分析过程中不断改变初始状态模型中指定优化目标区域的材料性质参数或单元性质参数，从目标区域中增加或减少单元，在指定约束条件下迭代直至达到目标函数指定值或满足约束条件时停止，获得最优设计结果。设一个目标函数由n个设计响应(即优化分析的输入量)组成，最小化n个设计响应φi的目标函数可表示为：

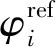
约束可表示为：

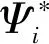
优化问题可表示为：

Ω=min[Φ(U(x),x)]

式中：Φ为以状态变量U与设计变量x为自变量的目标函数。

根据上述模型计算结果，采用一般算法建立拓扑优化任务：1) 冻结拉索水平分力荷载区域(齿块区域)，按法线更新密度，最小密度(系数)为0.001，最大为1，指定每个设计循环最大密度改变量不超过0.25。2) 创建基于刚度的拓扑优化设计响应，分别以优化区域应变能与体积为变量。3) 所有单元的应变能之和是结构柔度的度量，最小化柔度可使全局刚度最大化。以最小化应变能(柔度)为目标函数，指定约束(设计响应目标)为体积小于等于10%，即当体积减小到10%时停止优化。经过33次迭代循环，得到索塔在斜拉索水平分力作用下拓扑优化构型(见图4)。

图4 拓扑优化构型

2.3 拉压杆模型

根据上述拓扑优化构型，可明确荷载传递的主要路径，这与壳单元建立的横截面上第一主应力迹线的大致趋势一致。通过主应力分布对应力进行积分，使拉压杆轴线位于应力图合力的中心处，各杆件交点即为拉压杆模型各节点的位置。各杆件尺寸见图5(对称结构，仅显示1/2拉压杆模型)，其中 OA、AB、BE杆件为拉杆，其余为压杆。

图5 拉压杆模型尺寸(单位：mm)

将最大拉索水平分力作用于F、F′上，得到各杆件内力。根据所需钢束面积As(As=F/θσcon，其中F为杆件轴力，θ为安全系数，σcon为张拉控制应力)求得各拉杆对应的钢束面积(见表1，因DF及D′F′位于齿块区域，其拉压杆模型内力不作为预应力束设计的参考；轴力正值表示受拉，负值表示受压)。

按BE、B′E′杆件轴力计算所得钢束面积选配φs15.2-17钢束，设置U形环向预应力束u1、u2及直线预应力束l，按图6所示进行布置，各束预应力有效面积为2 380 mm2。

表1 各杆件轴力及所需钢束面积

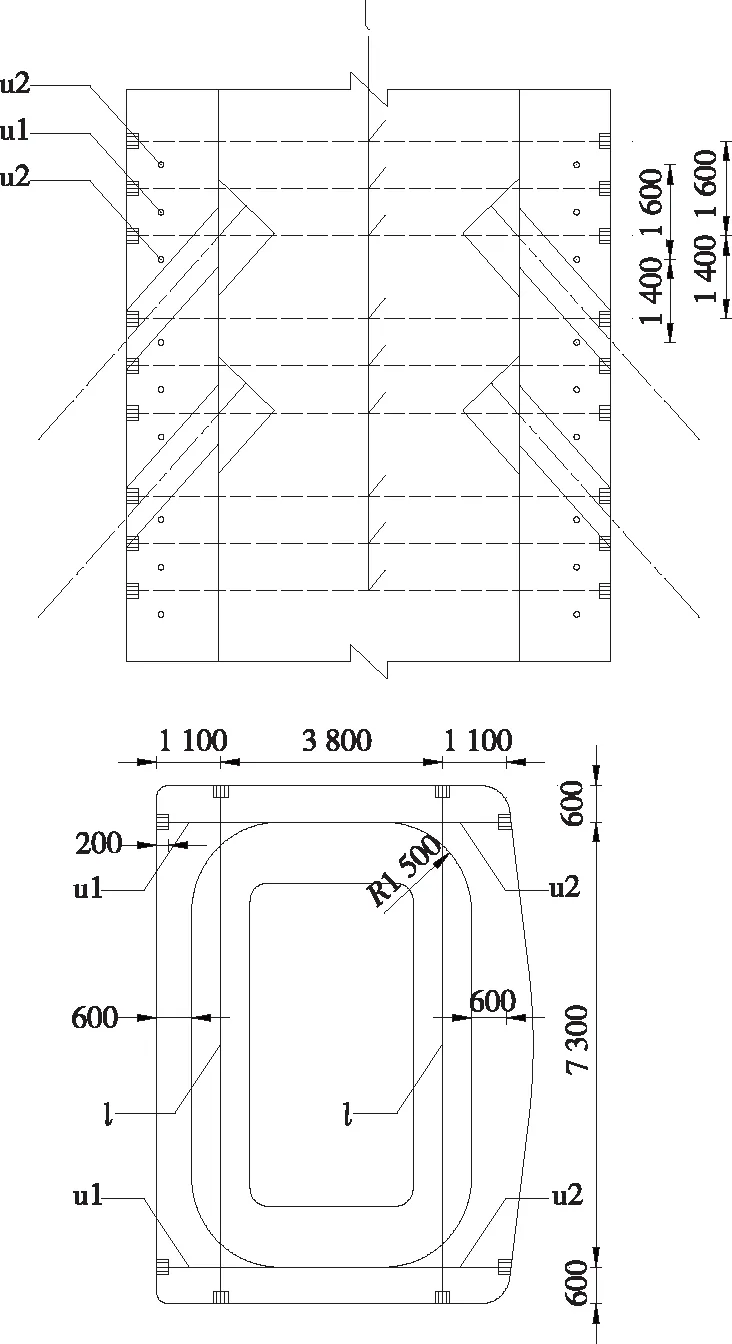
图6 预应力束布置示意图(单位：mm)

3 配束方案验证

3.1 实体模型建立

建立三维实体模型，索塔节段采用C3D20R单元模拟[见图7(a)]，C3D20R能在一定程度上减弱预应力束引起的索塔节段应力集中的影响；预应力束采用T3D2桁架单元模拟[见图7(b)]。两类单元采用内置区域方式耦合，实现预应力束与砼索塔的相互作用。根据沈璐等的研究成果，对于小半径预应力 U形钢束，双端张拉时，钢束中间直线段处的剩余应力为初始应力值的75%。若取张拉控制应力为1 395 MPa，则钢束直线段的剩余应力为1 046.25 MPa。再计入砼弹性压缩损失，得出各计算位置的有效预应力值。采用降温法对预应力束施加预应力，按下式计算模拟预应力的等效温度：

ΔT=σ/Eα

式中：σ为有效预应力；E为预应力束弹性模量；α为预应力束的线膨胀系数，取1.2×10-5。

将斜拉索索力换算成均布荷载施加于锚固齿块锚固面上，使荷载合力与拉索索力的大小、方向一致。材料参数见表2，未考虑普通钢筋与劲性骨架的作用。

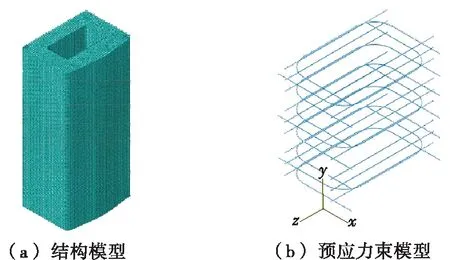
图7 索塔三维实体模型

表2 材料参数

3.2 实体模型计算结果分析

对实体模型进行静力分析，得到索塔砼部分第一、三主应力(见图8，正值为拉应力，负值为压应力)。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》，C55砼的抗拉强度标准值为2.74 MPa。

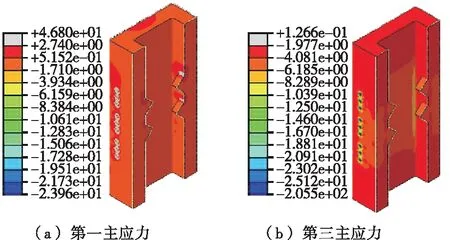
图8 索塔三维实体应力云图(单位：MPa)

由图8可知：1) 第一主应力存在部分超限的情况。超限较多的部分主要集中在预应力束锚固处以预应力束锚固点为中心的半径250 mm的圆内(图8中塔壁外侧灰白色部分)，最大达46.8 MPa。这是由于模型中未建立锚垫板等结构，预应力束与索塔采用内置区域形式建立相互作用，导致在预应力束端部引起应力集中情况。而实际构造中并不会产生如此大的拉应力，故该处应力超限现象可予以忽略。超限较少的部分处于锚固齿块与塔壁内侧相交处，最大拉应力为5.2 MPa。这一方面是由于模型中两构件相交为一钝角，几何上存在突变现象，产生应力集中；另一方面实际构造中主要通过普通钢筋解决齿块开裂问题，该模型未考虑普通钢筋的作用，实际结构中添加普通钢筋予以补强可解决齿块受力问题。除上述两部分应力超限外，索塔其余绝大部分第一主应力均低于0.5 MPa，最小值为-24.0 MPa，均满足C55砼抗拉、压强度要求。2) 第三主应力最大值约为-0.1 MPa，最小值为-205.5 MPa，主压应力偏大的原因同样在于预应力束锚固处产生应力集中，超限较多的部分主要集中在预应力束锚固处以预应力束锚固点为中心的半径250 mm的圆内。实际结构中由于锚垫板的存在不会出现如此大的压应力。除预应力束锚固处外，索塔其他砼部分第三主应力均为-0.1～-25.1 MPa，满足C55砼抗压强度要求。

对于索导管导致的预应力束盲区，可采取增加预应力短束的方式加以补强。增加短束前后塔壁外侧中心轴线应力沿高度方向的分布见图9，以第一个齿块顶部为x坐标轴原点，向下为负方向。

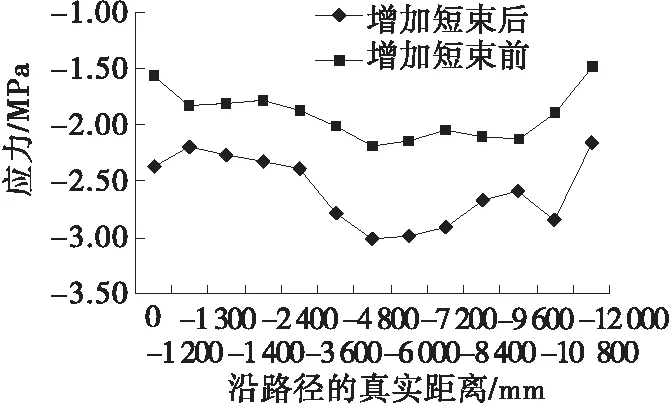
图9 塔壁外侧中心轴线应力沿高度方向的分布

由图9可知：增加短束后，塔壁外侧压应力相较于增加短束前大幅提高，增加了索塔应力储备，最大压应力储备提高0.86 MPa左右，最小提高0.37 MPa左右，应力分布较均匀，提高了结构抗拉能力。

综上，采用拓扑优化明确荷载路径，建立拉压杆模型换算预应力配筋面积进行索塔锚固区预应力配束的方法可行。

4 结论

(1) 对于给定结构与给定设计响应目标、约束，采用渐进拓扑优化方法能实现结构的拓扑优化，产生明确荷载传递路径的拓扑构型，指导拉压杆模型建立。

(2) 拉压杆模型与结构应力迹线较一致，说明拓扑优化构型指导拉压杆模型建立的方法适用。

(3) 采用由上述方法得出的配束方案，索塔砼节段第一主应力与第三主应力基本满足砼抗拉、压强度要求，部分应力集中区域与锚固齿块区域采用锚垫板、普通钢筋等构造方法可避免应力集中，减小结构主拉应力、主压应力偏大的情况。总体而言，采用文中方法对预应力束进行设计可行。