-超曲面的一个积分等式

李云川, 刘 燕 , 魏国新

(1. 河南交通职业技术学院商务旅游系, 郑州 451460; 2. 郑州航空工业管理学院数学学院, 郑州 450046;3. 华南师范大学数学科学学院, 广州 510631)

令X:M→n+1是(n+1)-维欧氏空间中的n-维光滑超曲面. 2018年，CHENG和WEI[1]引入了保加权体积的平均曲率流，具体为：称一类满足X(·,0)=X(·)的光滑浸入X(·,t):M→n+1为保加权体积的平均曲率流，若满足下面的方程

(1)

其中

H(t)=H(·,t)、N(t)、H(t)分别表示超曲面Mt=X(Mn,t)在点X(·,t)处的平均曲率向量、单位内法向量、平均曲率，N是X:M→n+1的单位法向量. 可以证明方程(1)保持如下定义的加权体积V(t)：

加权面积泛函A:(-ε,ε)→定义为

其中,dμt是X(t)诱导度量下M的面积元. 令X(t):M→n+1是X的变分，其中X(0)=X. 若V(t)是常数，称X(t):M→n+1是X的保加权体积的变分.

CHENG和WEI[1]证明了:对所有的保持加权体积的变分来说，X:M→n+1是加权面积泛函A(t)的临界点的充分必要条件是存在常数满足

〈X,N〉+H=,

(2)

其中，H为M的平均曲率;并给出-超曲面的定义：如果一个浸入超曲面X:M→n+1满足方程(2)，则称之为-超曲面. 随后，学者们得到了若干有关-超曲面的刚性定理和分类定理[2-12].

关于0-超曲面的研究，已有很多好的结果. 如，LE 和 SESUM[13]证明了:若M是 (n+1)-维欧氏空间中的n-维完备的具有多项式面积增长的嵌入自收缩子并且满足S<1，则S=0且M就是超平面n，其中S表示第二基本形式的模长平方；CAO和LI[14]研究了更广泛的情形并证明了：

定理A若M是(n+1)-维欧氏空间中的n-维完备的具有多项式面积增长的自收缩子并且满足S≤1，则M要么是超平面n，要么是圆球面要么是柱面n-m，1≤m≤n-1.

n-维欧氏空间n、n-维球面Sn(r)和n-维柱面Sk(r)×n-k都是-超曲面，其的值分别为0、n/r-r和k/r-r. CHENG和WEI[1]证明了：若M是n-维完备的具有多项式面积增长的嵌入-超曲面，且满足H-≥0和(f3(H-)-S)≥0，则M只能是Sk(r)×n-k(0≤k≤n)，其中j是M的主曲率. CHENG等[2]分类了具有多项式面积增长的且平均曲率H和第二基本形式长度平方S满足一个不等式的完备-超曲面，并得到了没有多项式面积增长这一条件的刚性结果.

1 预备知识

首先，介绍文中所用的基本公式. 令X:Mn→n+1是(n+1)-维欧氏空间n+1中的n-维连通的超曲面. 取局部标准正交标架场其对偶为要求限制在Mn上时，e1,…,en是Mn的切平面的基底. 则

限制在Mn上有

其中，hij表示X:Mn→n+1的第二基本形式的分量，是平均曲率.是X:Mn→n+1的第二基本形式，N=en+1是单位法向量. 令hijk=khij,hijkl=lkhij,其中,j是协变微分算子. Gauss 方程、 Codazzi 方程和 Ricci 方程分别为

Rijkl=hikhjl-hilhjk,

(3)

hijk=hikj,

(4)

(5)

其中,Rijkl是曲率张量的分量. 一个函数F的协变导数可以表示为F,i=iF,F,ij=jiF. 对于-超曲面，我们定义一个椭圆算子如下：

(6)

其次，给出本文定理证明需用的引理.

引理1[15]令X:M→n+1是完备的超曲面. 若u和v是C2函数,且满足

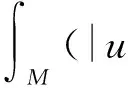
(7)

则

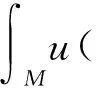
(8)

引理2[1]若X:M→n+1是-超曲面，则

(9)

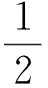
(10)

2 主要结论及其证明

定理1若X:M→n+1是n-维完备的具有多项式面积增长的-超曲面且满足S有界，则

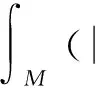
其中,H是M的平均曲率，S是M的第二基本形式模长平方.

证明因为 〈X,N〉+H=，则

(11)

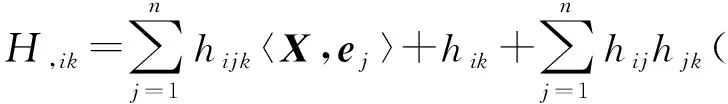
(12)

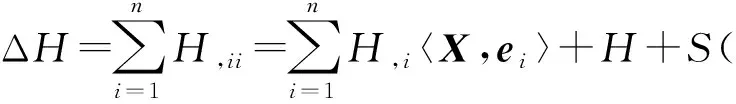
(13)

由引理2可知

(14)

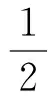
(15)

因为S有界，则H2和S(-H)H有界. 因为M具有多项式面积增长，则由-超曲面的定义以及式(11)，有

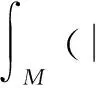
(16)

有界. 由引理 1、式(15)得到：

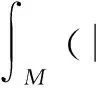
(17)

推论1若X:M→n+1是n-维完备的具有多项式面积增长的-超曲面且满足S有界和

(H-)2S≤H(H-),

(18)

则M要么是超平面n，要么是圆球面Sn(r)，要么是柱面Sk(r)×n-k(1≤k≤n-1).

证明由定理 1 以及已知条件 (H-)2S≤H(H-)，可得

(H-)(H+S(-H))≡0

(19)

和H为常数. 若H-≡0，由式(9)得到H=≡0，则M是超平面[14]. 若H≢，由式(19)可知S=H/(H-). 此时，式(12)变为

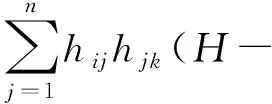
(20)

式(20)两端同乘hik，并对i和k求和，可以得到

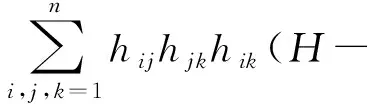
(21)

即

(22)

由引理2和式(22)可知

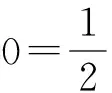
(23)

由此知道M是等参超曲面且M要么是圆球Sn(r)，要么是柱面Sk(r)×n-k.

注记1本文仅以定理1和推论1为例来说明如何得到-超曲面的积分等式和刚性定理. 事实上，用类似的方法可以得到一些类似的积分等式和刚性定理.