大整数除法器硬件电路研究与实现
2020-08-08王德明骆开庆
王德明,骆开庆
(华南师范大学物理与电信工程学院∥广东省心脑血管个体化医疗大数据工程技术研究中心,广州 510006)
公钥密码算法已被广泛应用于区块链、安全芯片、智能卡以及NFC等技术中以增强安全性,其中一个必不可少的算法是大整数除法[1-3]. 与模加、模乘和模幂运算相比,除法的使用频率较低,主要用于CRT中国剩余定理、素数产生以及蒙哥马利预处理等.
传统的大整数除法是通过软件迭代的形式反复调用处理器内部的8/16/32位通用短整数硬件除法器[4-5],继而实现大整数的运算,当整数的位数达到2 048位甚至4 096位时,这种做法需要耗费大量的时钟周期[6]. 由于公钥协处理器的主频较低,如在智能卡片内的工作频率不超过30 MHz,因此,使用软件实现大整数除法将耗费过长的计算时间,不利于即时通信,有必要将该算法硬件化,以缩短计算时间. 现有关于硬件除法器的研究主要是基于短整数的算法和电路,例如数字递归[7]、浮点除法[8]和函数迭代[9],此类方法适用于通用处理器内部的除法电路,其位宽可以是8、16、32、64位,随着位宽的增加,电路时延和面积也在增大,以至于难以直接使用上述方法实现大整数硬件电路.
为加快大整数除法的运算速度,本文提出一种适合硬件实现的低功耗大整数除法快速算法及其硬件电路,将2个大整数分别存储在SRAM随机访问存储器中,结合内部控制器和状态机,以期实现高速数据读取和除法计算.
1 大整数除法快速算法
1.1 传统的不恢复余数除法算法
大整数除法算法可以表示为:
X=D×Q+R,
(1)
其中,X是n位的被除数,D是m位的除数,Q和R分别是商和余数. 为避免使用硬件资源消耗多且计算时间长的除法运算,可采用不恢复余数除法算法(算法1),该算法只需加减法和移位操作即可求出商和余数[10].

算法1运行时需要在循环内判断X是正数还是负数,并作出相应的减法或者加法,每次移位相减后得到一位商,循环结束后应根据符号调整X的值,从而得到最终的商和余数. 可以看出,完成一次除法需要用到3个存储器,分别存放X、Q和R,电路面积较大. 此外,由于X是大整数,使用寄存器存放将导致较大的功耗和面积. 目前普遍的做法是采用SRAM随机存取存储器存放较大的数据,而这种做法的弊端是数据只能按字读取,速度较慢. 假设存储器的字长为w位,那么仅仅完成一次移位最少都要耗费n/w个时钟周期,当循环次数较大时不利于除法的快速计算.
1.2 适合硬件实现的低功耗大整数除法快速算法
为降低电路面积,提高算法计算效率,本文提出适合硬件实现的低功耗大整数除法快速算法(算法2),运用该算法,可以有效地提高并行度、降低移位操作所需时间,且除了最终处理需要使用2个存储器之外,被除数每一次循环产生的商和余数均存放在同一个存储器中,特别适合硬件实现. 计算时在被除数X的最高位添加1位的0,并将其分成2个部分,分别是X′和X″,其中X′的长度和除数D一致. 此时,移位运算的长度不再是原来的n位,而是除数D的长度,因此,每次移位时,可先读取X″[n-m-j]并将其移进X′中. 与算法1相比,算法2可以降低一半的移位时间,并且移位时可同时执行加减操作,大幅提高并行度,即移位和加减法可以在同一个时钟内完成. 执行完一次循环后,根据X′的符号决定商为1或0,并将商写进X″[n-m-j],从而节省硬件资源. 全部循环完成后,X″就是商,余数则存放到D,全部计算过程只需1个n位的存储器和1个m位的存储器.

完成移位后需要做大整数加减法运算,当数据长度较大时很难在一个时钟完成,为降低加减法电路的面积和延时,可考虑以字为单位进行计算. 假设w为存储器的字长,且n和m均能被w整除,则被除数、除数、商和余数可以表示为:
(2)
(3)
那么,完成一次大整数加减法需要m/w个时钟周期,完成一次除法的时间数量级为(n-m+1)·m/w. 假设被除数是1 024位,除数是512位,存储器字长为32位,则一次除法大约需要8 208个时钟周期,对于13.56 MHz主频的时钟来说,需要花费0.6 ms的计算时间. 若采用软件计算,数据的读写、移位和加减法需要经过多个时钟周期,花费时间将是硬件的几十倍,对片内工作频率较低的芯片来说难以接受.
图1显示了被除数、除数、商和余数的存放位置. 其中,存储器的字长为w,被除数X一共有n/w个字,存放在RAMX存储器中;除数D一共有m/w个字,存放在RAMD存储器中. 在除法运算的过程中,RAMX存储器的高位存放每一轮循环产生的临时余数,低位存放商. 完成除法运算后,余数R存放在RAMD中;原被除数的高位清零,低位存放商Q,一共有(n-m)/w个字. 可以看到,利用算法2可以高效利用存储器实现分时复用,大幅降低了存储电路面积.
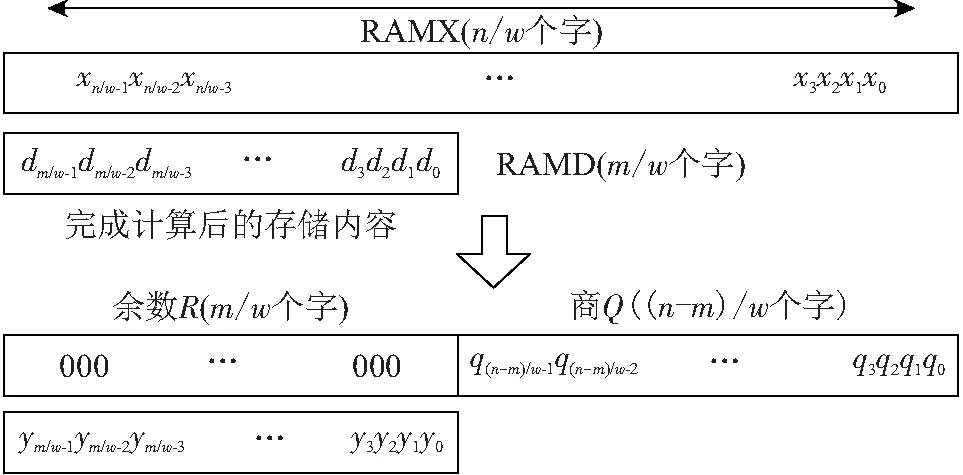
图1 变量与存储器的对应关系
1.3 适合硬件实现的低功耗大整数除法快速算法性能分析
当除法器硬件电路的频率确定后,运算时间可以用时钟周期来表示. 除法器运算时间与存储器字长有关,由图2可知:存储器的字长越长,完成一次除法所需的运算时间越短. 例如,当存储器的字长为8位时,完成一次1 024位除以512位的操作需要3万多个时钟周期,而采用32位存储器时需要8 000多个时钟周期,采用64位时只需要4 000多个时钟周期.
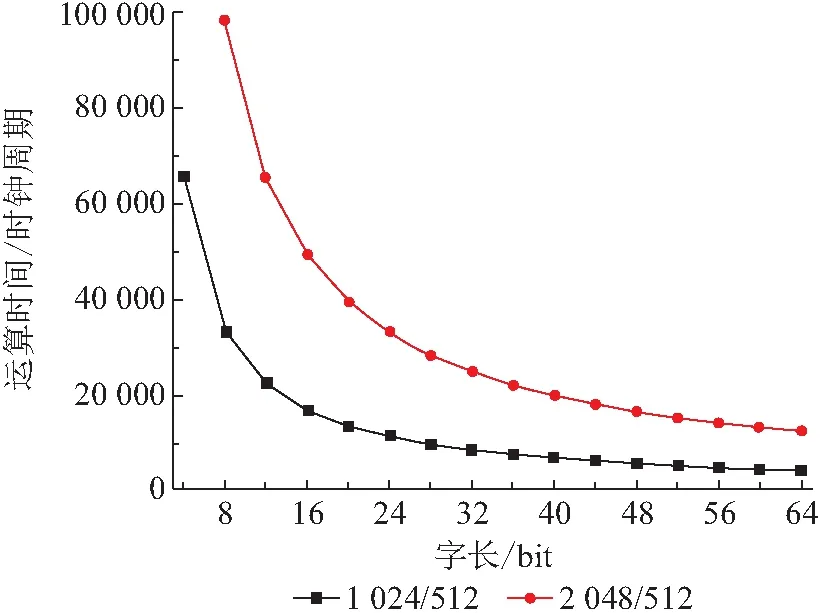
图2 除法器运算时间与字长的关系
由图3可以看出:存储器消耗的电流随着存储器大小和字长的增加而增加. 例如,对于4 096位的存储器,采用8位字长,电流大约73 μA;采用32位字长则上升到110 μA;采用64位字长的电流更大,高达153 μA. 此外,字长增大将导致存储器的面积增加,因此,不能通过无限制增加存储字长w来缩小单次除法的运算时间.
基于上述分析,本文拟采用32位字长来设计存储器.
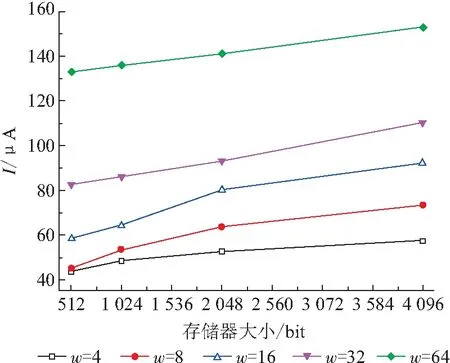
图3 存储器大小与电流的关系
2 低功耗大整数除法器硬件电路
基于算法2,设计了大整数除法器硬件电路(图4),其中,clk为大整数除法器硬件电路的时钟信号,控制存储器的读写时序以及寄存器的工作;rst为复位信号,用于寄存器的清零操作;en为除法器使能信号,该值为高电平时,除法器开始工作;func为功能选择信号,有8种不同的计算功能,包括不同位宽的除法和求模功能. 通过datain可以从外部接口电路写数据到RAMX和RAMD存储器中,当除法器运算完毕,可以从dataout获取存储器存放的商或余数.
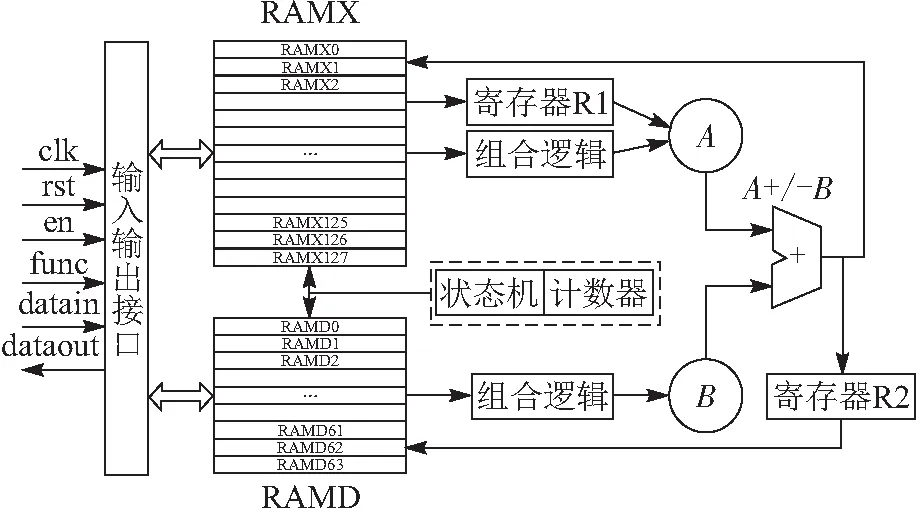
图4 大整数除法器硬件电路结构
如图4所示:(1)外部电路与除法器之间传输数据需要通过输入输出接口,除法运算前需要将被除数和除数写进存储器RAMX和存储器RAMD中,其中,存储器RAMX是一个字长为32位、深度为128的随机存储器,存储器RAMD则是一个字长为32位、深度为64的存储器. 为了获得更高的吞吐率,存储器均采用双端口结构,可以在上升沿的时候读取数据,下降沿的时候写入数据,1个时钟周期内就可以完成1次读写操作. 此外,为了同时读写2个存储器,应单独设计2套接口电路,同时提供地址和数据. (2)为了获得除法或者求模结果,电路在状态机和计数器的控制下,将存储器RAMX中的数据取出,经过处理后存放到寄存器R1,该值用来形成加法器的输入参数A. 存储器RAMD中的数据取出后,经过逻辑电路处理后直接形成加法器的输入参数B. 加法器将根据上一轮加减法的结果,判断X是正数还是负数. 如果是正数,则执行减法操作;如果是负数,则执行加法操作. 加法器的结果将写回存储器RAMX中,作为临时保存的数据. 全部计算完毕后,存储器RAMX将存放商,存储器RAMD将存放余数.
下面给出除法计算过程举例,以理解算法2的计算过程. 假设X是16位的被除数,D是8位的除数,在计算时,将X分成2个部分(X′和X″),其中,X′是8位的临时寄存器,X″用来存放每一轮计算产生的商,每轮计算后均需要左移一次,将X″的最高位移位到X′的最低位,经过9轮计算后,最终得到商和余数,分别写到X和D中(图5).
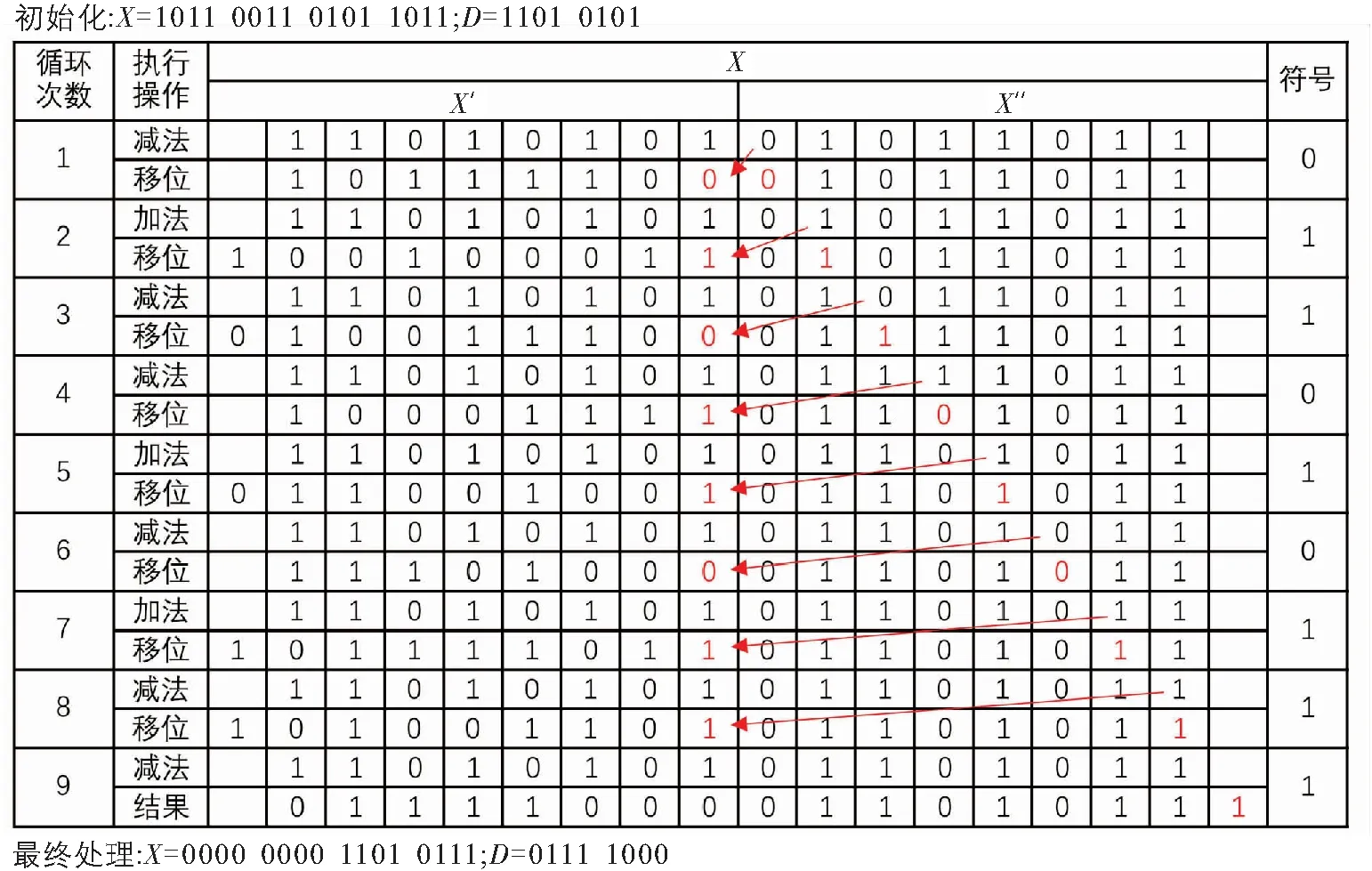
图5 除法计算过程举例
除法电路需要用到32位的加法运算单元,从而实现移位相减或相加的计算. 加法器分为行波进位加法器、CSA加法器和超前进位加法器. 其中,行波进位加法器原理较为简单,设计复杂度小,具有面积小和功耗低的优势,但延时太大;CSA加法器可以将3个数相加的和用2个数来表示,但实际上并没有真正解决2个数相加产生1个输出的问题,因此不能用在大整数除法器硬件电路中;而超前进位加法器的进位是各自独立且同时产生的,虽然逻辑复杂度较高,但高一位的进位不依赖低位的进位产生与传送,运算速度快,延时小,因此,本文拟采用超前进位加法器降低电路延时.
3 大整数除法器硬件电路的功能和性能分析
本文提出的大整数除法器硬件电路具有8种大整数除法和求模功能(表1),当功能选择信号(func)从000到011时,可以实现除法和求模运算,其中,X代表被除数,D代表除数,在计算之前,应将输入数据写入存储器RAMX和RAMD中,激活硬件加速器,完成除法后,商和余数均存放到存储器RAMX中. 本文提出的大整数除法器硬件电路最高可支持4 096位的被除数和2 048位的除数. 当除数较小时,可以选择合适的位宽,减少计算时间. 除法运算可用于1 024位或2 048位 的RSA-CRT,模运算可用于模乘或素数生成的预计算. 这些运算可广泛应用于RSA公钥密码算法和ECC椭圆曲线密码算法.
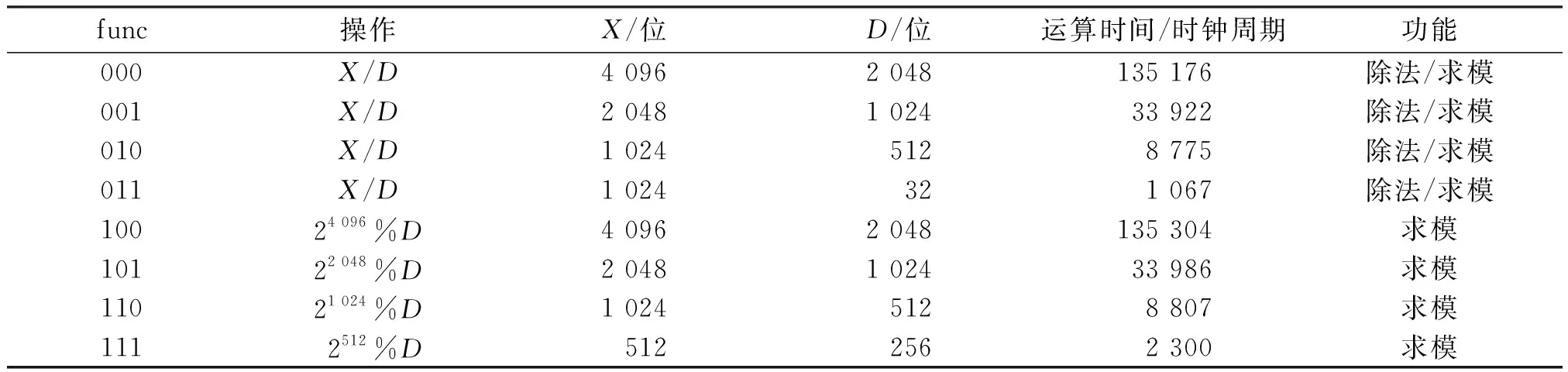
表1 大整数除法和求模功能Table 1 The division and modulus function for big integers
下面采用0.13 μm CMOS工艺,对大整数除法器硬件电路进行评估. 由于除法器主要针对智能卡或NFC设备设计,因此,本文使用了3种不同的频率来分析:13.56 MHz(非接触式智能卡)、30 MHz(接触式智能卡的最大频率)和125 MHz(电路可工作的最大频率). 由功耗和面积的评估结果(表2)可知:(1)功耗随着频率的增加而增加. (2)在3种频率(13.56、30、125 MHz)下,总功耗分别约为117、201、715 μW,远远低于智能卡或NFC设备提供的总功率(3~50 mA)[11]. (3)除法电路面积最大的是RAM存储器,这是由于需要存放较大的整数,所以这部分面积是难以节省的,即使采用软件计算,也需要将被除数和除数存放在内存中;除了存储器以外,除法器的逻辑控制电路面积并不大.

表2 大整数除法器硬件电路的频率、功耗和面积之间的关系Table 2 The relationship among frequency, power consumption and area
通过使用自动布局布线和版图设计工具,可以得到大整数除法器硬件电路的版图(图6). 利用版图工具可知大整数除法器硬件电路的总面积为0.12 mm2. 由图可知:与控制电路的小面积相比,存储器占据了大部分版图,这意味着该算法具有相对较低的逻辑复杂度.
为了体现本文的低功耗大整数除法快速算法及其硬件电路在面积和功耗方面的优势,把本文的大整数除法器与Iterative除法器[1]、Radix-16除法器[4]、Binary64除法器[12]及Radix-8除法器[13]进行对比. 为了公平比较,在功耗方面,采用每兆赫的功
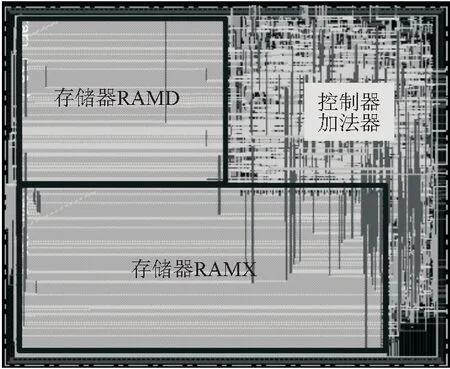
图6 大整数除法器硬件电路版图
耗来评估大整数除法器硬件电路是否具有低功耗的优势;在除法器硬件电路的面积方面,使用每位占用的面积进行评估. 由比较结果(表3)可知:大整数除法器的硬件电路占用极低的功耗和面积,每兆赫兹消耗的功耗为10 μW,总面积为0.12 mm2,其中每位占用的面积为120 μm2.

表3 不同除法器的性能对比Table 3 The comparison of power consumption and area between the proposed hardware circuit and others
4 结论
本文提出了一种基于不恢复余数除法算法的低功耗除法器硬件电路,该电路可广泛应用于公钥密码算法的计算中. 所提出的低功耗大整数除法快速算法及其硬件电路支持多种位宽的除数和被除数,可为公钥协处理器提供除法和求模运算功能,最高可支持4 096位的被除数以及2 048位的除数. 使用0.13 μm CMOS工艺,对该大整数除法器硬件电路进行评估和验证,结果表明:该电路的主频最高可达125 MHz,总面积为0.12 mm2,每兆赫兹消耗的功耗为10 μW.
