“多题一解”在教学中的应用

张 岭

（广东省深圳市新华中学 广东深圳 518109）

所谓“多题一解”，就是指从一个角度思考，用同一种方式来解答不同的问题[1]，即探究问题的本质，归纳、总结它们的相同点，从而提炼出解决多道同类题目的方法，形成“多题一解”。

“多题一解”有助于培养学生的归纳总结能力，可以帮助他们找到不同问题的本质、核心，做到融会贯通[2]。这样，在思考、讨论、解答问题的过程中，学生学习的积极性被充分调动起来，既开阔了他们的思路，又培养了其数学思维能力，能有效地激发学生的学习兴趣，让学生感受到数学的乐趣。

在解答题目的过程中，学生利用“多题一解”的数学思想，对题目进行了充分比较，发现了题目的本质。这有利于加深学生对知识的理解，也培养了他们的归纳、总结能力。下面用一个例子来说明。

北师大版七年级下第二章“相交线与平行线”中有一类比较典型的题目，如下所示。

例1 如图，已知直线l1∥l2，点P在直线l3上，且不与点A、B重合，记∠AEP=∠1，∠PFB=∠2，∠EPF=∠3。

（1）当P点在图1位置时，试说明∠3=∠1+∠2。

（2）当P点移动到图2位置时，请写出∠1、∠2、∠3之间的关系，并说明理由。

（3）当P点移动到图3位置时，请写出∠1、∠2、∠3之间的关系，并说明理由。

图2

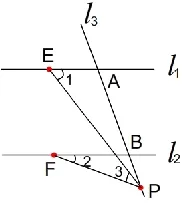
图3

分析：两条平行线被一个拐角联系在一起，可称为拐角问题。此题三个小题的解题思路是一致的，都是过拐点作平行线，再利用平行线的性质和判定，结合∠1、∠2、∠3的位置关系，得出∠1、∠2、∠3之间的数量关系。下面是具体的解法。

（1）下面是图1问题的证明。

证明：如图4，过P点作直线PQ∥l1

∴∠EPQ=∠1(两直线平行，内错角相等)

∵l1∥l2（已知）

∴PQ∥l2（平行于同一条直线的两条直线平行）

∴∠QPF=∠2（两直线平行，内错角相等）

∵∠3=∠EPQ+∠QPF

∴∠3=∠1+∠2

总结：通过过P点作直线PQ∥l1，把两条平行直线l1和l2联系起来。

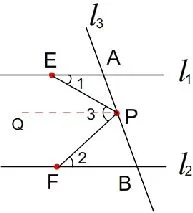
图4

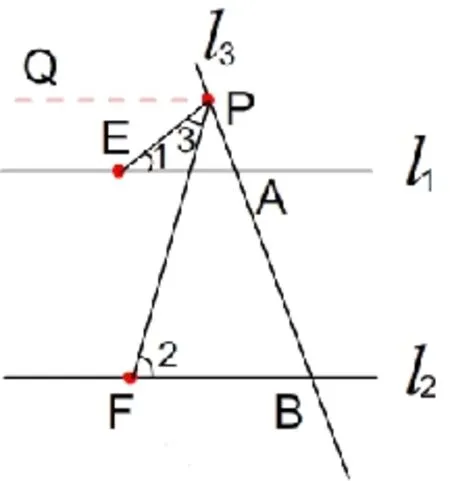
图5

（2）下面来看图2问题的证明。

解：∠2=∠1+∠3

理由是：

如图5，过P点作直线PQ∥l2

∴∠FPQ=∠2(两直线平行，内错角相等)

∵l1∥l2（已知）

∴PQ∥l1（平行于同一条直线的两条直线平行）

∴∠EPQ=∠1（两直线平行，内错角相等）

∵∠FPQ=∠EPQ+∠3

∴∠FPQ=∠1+∠3

∴∠2=∠1+∠3

通过上面两个小题的证明，我们可以发现：类似的题目，都可以通过拐点作与已知平行线相平行的辅助线的方法来解决。

对图3问题的证明，可以用与图1、2类似的方法，由学生自己完成，组内讲解、订正。

接下来，教师要提问：请考虑，作辅助线可不可以写作“过点P作PQ∥l1∥l2”？

在多年的教学过程中，笔者发现，很多学生像上面这样作辅助线，原因是不知道这与“过直线外一点有且只有一条直线与已知直线平行”相矛盾。

这样一题三问初步加深了学生对此类问题的理解。下面，我们把这个角拉到外面来，看这种方法是否仍然可行。

例2 如图6，已知AB∥CD，探究∠A、∠APC和∠C之间的数量关系。

分析：这道题与例1形式不同，也有多种题法。能用上面的方法来解决这道题目吗？此题也是两条平行线被一个拐角联系在一起，我们试着用上题的方法来解一解。

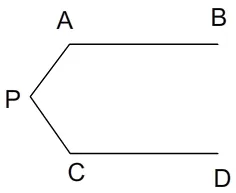
图6

解：如图7，过点P作PE∥AB

∴∠A+∠1=180°（两直线平行，同旁内角互补）

∵AB∥CD（已知）

∴PE∥CD（平行于同一条直线的两直线平行）

∴∠C+∠2=180°（两直线平行，同旁内角互补）

∴∠A+∠1+∠2+∠C=360°

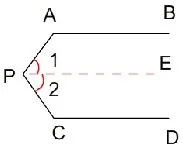
图7

即∠A+∠APC+∠C=360°

可以看出，例2的解法与例1的解法是一致的。在日常教学中，教师应教会学生掌握基本的解题模式和方法，形成必要的解题技能，掌握一定的探索数学问题的工具，升华为“多题一解”。

我们再来看与三角尺有关的题目是不是也和上面的题目有关。

例3 如图8，直线a∥b，直角三角形ABC的顶点B在直线a上，∠C=90°，∠β=55°。求∠α的度数。

分析：这道题只要过点C作CD∥b，就能转化为前面的题型了。

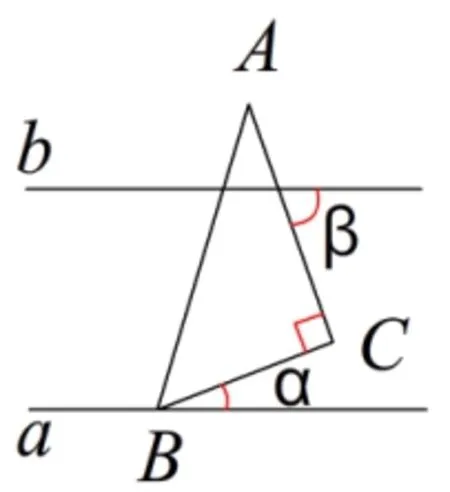
图8

通过上面的讨论，我们可以看到，很多题目虽然形式不同，但可以用同一种方法解答，也就是“多题一解”。“多题一解”思想的作用是培养学生分析题目内在联系的能力，让学生学会看到一道题就想到一类题、想到相应解法[3]。这种方法可以帮助学生进行归类、总结，深入分析此类题目的解法，不至于一道题目一种解法，搞得学生无从下手。

“多题一解”是培养学生创新思维能力的有效途径之一。要想达到数学上的“多题一解”，学生必须在平日多下功夫，先尽可能地积累“多题一解”的技巧，最终对数学融会贯通，加深对问题本质的理解。