集对分析阴阳平衡方程在皮肤病诊治中的应用

卢怡 蒯仂 茹意 罗月 许逊哲 徐蓉 李欣 赵克勤 李斌

摘要  目的：為依据阴阳学说开展皮肤病中医辨证论治提供一种决策支持用数学模型，以期促进中医皮肤病辨证论治理论的现代化。方法：把集对分析理论中的八元联系数对应于太阳经、阳明经、少阳经、太阴经、少阴经、厥阴经以及任督二脉，根据“阴阳平衡”机体正常运行原理，设定八元联系数各联系分量值各在1/8，建立集对分析的阴阳平衡方程。结果：从临床案例发现，患者皮疹疾患主要归于足太阳经和足阳明经，应用阴阳平衡方程得出失衡还处在“量变”的“+++”阶段，若辨证用药得当，可在短期内获得显著效果，和实际情况一致。结论：集对分析的阴阳平衡方程可作为辨证论治皮肤病的辅助模型，其他疾病的辨证论治过程中亦可借鉴应用该方程。

关键词  阴阳理论;皮肤病;辨证论治;六经学说;数学模型;阴阳平衡方程;集对分析;联系数

Preliminary Study on the Application of Yin and Yang Balance Equation Based on Set Pair Analysis in the Diagnosis and Treatment of Skin Diseases

LU Yi1，KUAI Le1，RU Yi1，LUO Yue1，XU Xunzhe1，XU Rong1，LI Xin1，ZHAO Keqin2，LI Bin1

（1 Yueyang Integrated Chinese and Western Medicine Hospital Affiliated to Shanghai University of TCM，Shanghai 200437，China; 2 Zhuji Institute of Contact Mathematics，Zhuji 311811，China）

Abstract Objective： To provide a mathematical model for decision support based on yin and yang theory，in order to promote the modernization of syndrome differentiation theory for TCM dermatopathy. Methods： First，as for the eight-element connection number in the set pair analysis theory corresponded to the Taiyang meridian，Yangming meridians，Shaoyang meridians，Taiyin meridians，Shaoyin meridians，Jueyin meridians and RenDu two meridians，according to the “Yin and Yang Balance” body normal operating principal，the value of each contact component of the eight-element contact number was about 1/8.When the patient was sick，the value of some contact components changes.The medication of syndrome differentiation and treatment was to restore these small or significant changes to normal physiological state; for this reason，the octal connection number was written as the equation of the left yin and right yang，called the yin and yang equilibrium equation based on set pair analysis.Combined the medical case in the literature，the clinical application of the equation was explained. Results： The solution to the yin-yang balance equation was appropriate to the yin-yang theory-based dermatological diagnosis and treatment method summarized in a literature.It was an intuitive mathematical model for decision-making support for TCM syndrome differentiation of dermatology. Conclusion： The yin and yang balance equation based on set pair analysis can be applied in the clinical diagnosis and treatment of skin diseases in TCM，and can be used as a decision support model for syndrome differentiation and treatment of skin diseases.The TCM clinical practice of other diseases can also learn from this equation.

Keywords  Yin and yang theory; Skin disease; Syndrome differentiation; The six classics; Mathematical model; Yin and yang balance equation; Set pair analysis; Number of contacts

中图分类号：R241;R242 文献标识码：A  doi： 10.3969/j.issn.1673-7202.2020.14.032

阴阳理论是中医辨证论治的一个基础性理论，历代中医医家在辨证论治各种疾病时创立的各种学说，说到底都是以阴阳理论为基础[1]。另一方面，从现代医学角度看，中医临床实践中面临的大量病患病例，离不开基于数学的统计分析和建立相应的数学模型[2-4]，以提高抽象思辨能力和辨证论治水平，最终提高临床疗效。数据挖掘涉及的学科领域和方法众多，基于此思考，我们在皮肤病中医用药选优研究中采用集对分析理论和方法取得若干成果的基础上，提出基于集对分析的阴阳平衡方程，结合我们的临床经验和相关文献，阐述该模型的创新思路和临床应用。

1 引言

阴阳属于中国古代哲学范畴中的一个概念：认为世间万物皆可分阴阳且阴阳互根。用现代哲学观点看，阴阳是关于对立统一事物的一种朴素指称。运用到中医中，有阴阳辨证之说，且为“八纲辨证”即“阴阳、寒热、表里、虚实”辨证之首，阴阳辨证统率其后的六辨，且一般把“热、表、实”归属阳，“寒、里、虚”归属阴;具体到中医诊治皮肤病，需要进一步通过症状、主诉、局部病变特征以及生化检查指标来辨证是阳证还是阴证，还是阴阳兼有，还是阳中有阴、阴中有阳等等;大致上，阳证多实多热，病程短，症状显著，相应的治则为清热、泻实;阴证多寒多虚，病程相应较长，宜温、宜托、宜补;此外还有“气为阳，血为阴”之说。临床上见到的银屑病，在南方，多呈现血热证，以凉血活血多能见效。把阴阳与十二经相联系，则得到阳经和阴经的概念。根据阴阳虚衰程度的不同，又分为太阳经、阳明经、少阳经、太阴经、少阴经、厥阴经，简称六经。加上主全身阴阳的任督二脈，可称为四阴四阳。据文献报道，我国当代中医皮肤性病学泰斗赵炳南先生擅长在皮肤病中医诊治中运用阴阳理论，为现代中医皮肤科的创建作出巨大贡献[5-7]。在临床中对一些疑难皮肤病辨阴阳脏腑后处方下药，收到卓著成效[8-10]。但迄今为止，难以检索到皮肤病临床应用阴阳理论方面的数学模型。

2 方法

2.1 集对分析 集对分析是我国学者赵克勤先生于1989年提出的一种处理事物确定性与不确定性关系的系统数学理论[11-15]，已在包括医药卫生统计和中医药优选和临床疗效评估等多方面得到广泛应用[16-18]。所谓集对，就是由2个集合组成的一个对子，这一思想与中医阴阳理论不谋而合，例如把3条阳经加上督脉组成一个集合A，把3条阴经加上任脉组成一个集合B，则由集A与集B组成的集对H=（A，B）就包含了六经和任督两脉。

2.2 八元联系数

联系数由我国学者赵克勤在创建集对分析理论时提出的数学概念[19-21]，是由二个或二个以上联系分量组成的结构函数，也是集对的特征函数，当把2个集合的全部关系分成确定和不确定两大类时，用方程

μ=A+Bi 1）

表示2个集合的全部关系，其中A是确定的关系数，B是不确定的关系数，i表示B的不确定性，在[-1，1]区间视不同情况的值，以说明B在多大程度上是正面倾向于A还是负面作用于A。

当B中的某些不确定关系存在极端负面作用时，改用三元联系数

μ=A+Bi+Cj 2）

作为集对的特征函数，这时，μ（2）中的j=-1，表示C代表的关系对于A具有极端负面作用，但又与A在同一个集对系统内;i仍在[-1，1]区间视不同情况取值，以说明B在多大程度上正面倾向于A，还是负面于倾向C，或以不同的比例分解B，以说明B中有一部分倾向于A，另一部分倾向于C。

对式2）中的Bi和Cj作进一步细分，可得到以下的四元、五元、六元、七元、八元等多元联系数：

μ=A+Bi+Cj+Dk 3）

μ=A+Bi+Cj+Dk+El 4）

μ=A+Bi+Cj+Dk+El+Fm 5）

μ=A+Bi+Cj+Dk+El+Fm+Gn 6）

μ=A+Bi+Cj+Dk+El+Fm+Gn+Ho 7）

式3）中的k=-1，j在[-1，0]区间取值，i在[0，1]区间取值，

式4）中的l=-1，k在[-1，-0.333]区间取值，j在[-0.333，0.333]区间取值，i在[0.333，1]区间取值

……

式7）中的o=-1，n在[-1，-0.666]区间取值，m在[-0.666，-0.333]区间取值，l在[-0.333，0]区间取值，k在[0，0.333]区间取值，j在[，0.333，0.666]区间取值，i在[0.666，1]区间取值。

由此可见，式1）到式7）中的联系数，第一项的系数始终是1，最末项的系数始终是-1，中间各项的系数i、j、k、l、m、n各自的取值区间依次是[-1，1]的均分子区间。对于式1）到式7），可以根据需要作归一化处理。以式（7）对应的八元联系数为例，可令A+B+C+D+E+F+G+H=N，称N为μ的联系范数，表示论域的大小（也就是所论2个集合在给定范围中的全部关系数）。

令a=A/N，b=B/N，c=C/N，d=D/N，e=E/N，f=F/N，g=G/N，h=H/N，则得归一化的八元联系数：

μ=a+bi+cj+dk+el+fm+gn+ho 8）

式8）中a+b+c+d+e+f+g+h=1，统称为联系数μ的联系分量，各联系分量的系数i、j、k、l、m、n、o取值同7）式，注意到a的系数是1，i、j、k都取正值，m、n、o都取负值，o=-1且a优先于（正于）bi，bi优先于（正于）cj，cj优先于（正于）dk，dk优先于（正于）el，el优先于（正于）fm，fm优先于（正于）gn，gn优先于（正于）ho，因此，若把式7）式8）放到阴阳学说的语境中，立即可以把A（a）看成是“太阳”（阳最强）的测度，B（b）看成是“阳明”（逊于“太阳”）的测度，C（c）代表“少阳”（阳气又略逊于“阳明”）的测度，D（d）则看成督脉（诸阳所汇）的测度，把dk看成是“少阴”的测度，把el看成是“太阴”的测度，把fm看成是“厥阴”的测度，若再借用数学集合论中的包含符号“”，就得到如下“阴阳矩阵”：

a+bi+cjD el+fm+gnH

a+b+c=d e+f+g=h  9）

式9）中的D代表督脉，统帅“太阳”“阳明”“少阳”三阳经，记为a+bi+cjD;用H代表任脉，统帅“少阴”“太阴”“厥阴”三阴经，记为el+fm+gnH。 令式（9）所属的六经加任督二脉之测度和为0（阴平阳秘）则有方程

a+bi+cjD el+fm+gnH

a+b+c=d e+f+g=h =0 10）

根据阴阳互根和阴阳平衡机体正常无病的观点，进一步由式10）提出机体无病症时的标准阴阳平衡方程：

a+bi+cjD el+fm+gnH

a+b+c=d= 1 2  e+f+g=h= 1 2  =0 11）

称式11）为基于集对分析联系数的三阴三阳加任督二脉的标准阴阳平衡方程，也简称阴阳平衡方程或平衡方程。其中的i、j在[0，1]区间的值待定，l、m、n在[-1，0]区间的值待定。也就是当a+b+c=d= 1 2 ，e+f+g=h= 1 2 时，i、j和l、m、n的值仍在各自的定义域作自适应、自变动、自调正，不难认同，上述假设性定义在整体上符合健康人体系统在正常情况下的实际运行状况。

在以上假定基础上，再进一步假定“太阳”“阳明”“少阳”“少阴”“太阴”“厥阴”，与任督二脈在病理状态下的变化可以分为自适应调整失控（微观层次上i、j和l、m、n的变化超出定义的范围）和病理上的宏观显现（各1/6的变大和变小）这样2个层次。

根据中医的“表里”理论和哲学上的量变质变原理，以及现代医学在生化检验时采用的符号表示法，这里再进一步约定式11）在机体病态情况下的2种表示方法：

1）在没有实质性的病变时，约定在六经二脉上的微小变化测度用加（+）号与减（-）号表示其程度。

如太阳病，若初起，则用一个加（+）号放置在代表太阳经的a=1/6的右上角，这时的平衡方程如下：

1 6 ++ 1 6 i+ 1 6 jD，el+fm+gnH

a+b+c=d= 1 2 ，e+f+g=h= 1 2  =0 12）

2）随着病情在太阳、阳明经上加重发展，则在相应的经脉测度上依次放2个加号“++”，3个加号“+++”，4个加号“++++”，5个加号“+++++”，最多用6个加号“++++++”表示;与此同时，用1～6个减号“-”表示在六经二脉上的衰退性病理变化。再根据各经脉上的加减号多少与用药理学知识，选用相应的中药，所用药物的量对应于i、j、k、l、m的数值和联系分量上的加减号多少，原则是要同时根据阴阳在含义和形式上的平衡。

2.3 阴阳平衡方程在皮肤病临床应用时的指证体系和综合计量

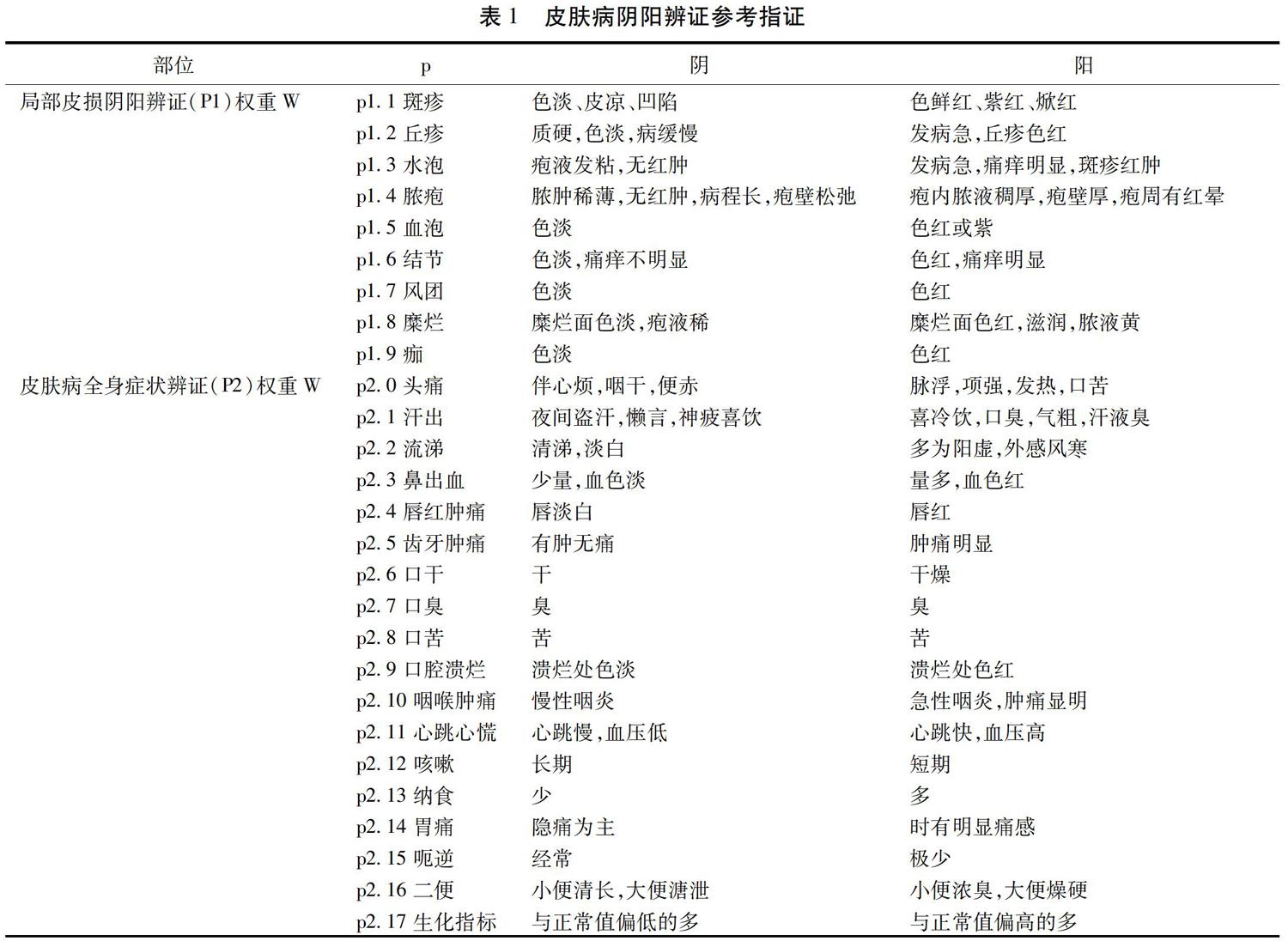
2.3.1 皮肤病阴阳辨证指证体系

2.3.2 阴阳辨证在阴阳平衡方程上的表示

由表1可见，皮肤病在局部皮损和全身症状2个大项指标上的阴阳辨证共有32个子项目，临床诊疗时，不仅需要借助望闻问切对这32个子项目作出阴阳辨证，并把结果定量地归结为1～6个“+”号，或直接在轻分量上作加减，而且还需要落实到某条阳经或阴经上，这前后两步称作为“定量归经加减”才能写出对应皮肤病患者某一皮肤病的阴阳平衡方程。这里，仅根据我们课题组的讨论给出以下建议。1）对P1和P2 2个一级指证的权重W1与W2设为区间值，以便于根据不同的辨证结果赋予具体的权重值。根据我们的临床经验，建议设为W1=[0.4，0.6]，W2=[0.6，0.4]，取值的约束条件W1+W2=1。2）设二级指证Pst（s=1，2，t=1，2）的权重为一级指证权重的均值，例如：对指证P1的权重取W1（P1）=0.4时，则W（P1）-W（P9）均为 0.6 9 ，与此同时有W2（P2）=0.6，则W（ρ2.0-ρ2.17）均为 0.6 18 ，等等。2）二级指证Pst中的各指证每出现一个，记为一个“+”号。3）归经原则，皮损原则：皮损在哪一条经络走行线上，则归于该经络;皮损在不同的经络线上时，平均分配“+”号数于这些经络。全身原则：按伤寒论所著落实归经。

3 案例

某，男，24岁，1997年10月9日初诊，病史，一周前去海边时咳嗽，过量食入海虾螃蟹等腥发食物。第2天夜间突然觉得双下肢轻度肿胀体痛，出现许多小红点，有的红点隆起，自服氯苯那敏3 d，红疹未退，色泽渐暗，稍加口干，便溏，3次/d，心烦躁。体检，双下肢自足至大腿可见密集状红色隆起 的丘疹，压之不褪色，小的有绿豆大小，以伸侧面为明显，双下肢轻度肿胀，舌质红，苔薄黄，脉滑数。血常规检查正常，尿常规检查正常，西医诊断：过敏性紫癜。中医诊断：葡萄疫。中医辨证：血热灼络，迫血妄行。治法：清热凉血，活血消斑。处方：紫草根16 g、茜草15 g、牡丹皮15 g、车前子15 g、泽泻15 g、半夏10 g、木瓜10 g、羚羊角粉0.6 g（冲服）。局部外用炉甘石洗剂。二诊，服上方14剂，下肢紫斑大部分色淡，肿胀明显消退，大便仍稀，痛有轻微加重。前方加白术，茯苓，白鲜皮，苦参续服。三诊，服前28剂，双下肢大部分皮损已基本消退，肿胀已无，便调，少许色素沉着伴轻度瘙痒，舌红苔白，脉弦滑。

此例过敏性紫癜是一种皮肤血管急性炎性反应，中医临床上分为“阳斑”和“阴斑”两大類，本例发病急，斑疹色红，心烦，口干，舌黄，脉数，为血热壅留，迫血妄行，血溢脉外，瘀滞凝结为斑，辨为阳斑。治以清热凉血，活血消斑而得效。

以上是文献[1-2]中对案例1的叙述，以下用给出的阴阳平衡方程加以梳理。

把临床诊疗中提到的症状与表1对照，确定量化值。见表2。

根据表2和临床诊断可知，其+++应放在足太阳经和足阳明经上，为此，由式12）得李某紫癜为阳斑的平衡方程为

1 6 ++++ 1 6 +++i+ 1 6 +++jD el+fm+gnH =0 13）

由式13）可见，患者皮疹疾患的阴阳失衡还处在“量变”阶段，且只有3个“+++”号，辨证用药得当，可在短期内获得显著效果，实际处方用药和临床效果如前。

4 讨论

《黄帝内经》曰：“诊者察色按脉，先别阴阳”。即临床辨证首辨阴阳，阴阳是纲，纲举目张，只有辨明阴阳，治疗上就不会犯原则性错误。阴阳有“度”，如何认识和刻画这个“度”？本研究，我们首次尝试使用相应的数学模型表述这个问题;但另一方面，每一首处方中的药都得有具体的用量，如何将“度”具体地落实在辨证论治的处方用药上，是未来我们研究方向之一。在中医阴阳理论与临证实践彼此尚有一些难以完全解释的模糊地带，我们提出的阴阳平衡方程试图为二者架起一座“桥梁”，这是我们的出发点，是我们的创新所在，也是一项难度极大的探索性工作，是否可以在中医临床实践中进一步推行？既有待积累临床资料，也有待模型本身的改进和完善，更有待众多行家与中医临床医生在实践中作进一步的摸索。

参考文献

[1] 徐晓楠，方钰发，王妍.中医阴阳与免疫的关系初探[J].四川中医，2019，37（2）：25-27.

[2]孙喜灵，郑秋生，林霞，等.中医证候结构表征研究及其前景展望[J].世界中医药，2015，10（2）：272-275，279.

[3]王益成，王萍，贾琼.基于中医临床理论的内容智能分发平台“信息茧房”系统量化模型研究[J].现代情报，2018，38（9）：36-40.

[4]邱瑞瑾，陈静，雷翔，等.引入核心指标集概念构建中医临床疗效模糊综合评价方法[J].中药新药与临床药理，2018，29（4）：528-534.

[5]赵炳南，张志礼.简明中医皮肤病学[M].北京：中国中医药出版社，2014：256-270.

[6]张志礼.跟名师学临床系列丛书[M].北京：中国中医药出版社，2010：321-322.

[7]李京玉.论皮肤病阴阳辩证[D].哈尔滨：黑龙江中医药大学，2012：143-146.

[8]胡雪晴，田野，屈双擎，等.基于文献数据挖掘分析寻常型银屑病血瘀证的方药证治规律[J].世界中医药，2019，14（10）：2655-2659.

[9]史宝娜.寻常型银屑病中医体质与中医证型的分布规律[J].中国药物经济学，2017，12（8）：146-148.

[10] 杨艳平.基于数据挖掘的治疗银屑病处方用药规律研究[J].世界中医药，2015，10（10）：1611-1613，1617.

[11]赵克勤.集对分析及其初步应用[M].杭州：浙江科技出版社，2000：9-42.

[12]赵克勤，偏联系数[M].北京：北京邮电大学出版社，2005：884-886.

[13]赵克勤，赵森烽.奇妙的联系数[M].北京：知识产权出版社，2014：28-30.

[14]蒋云良，赵克勤，刘以安，等.信息处理集对分析[M].北京：清华大学出版社，2014：23-25.

[15]刘秀梅，赵克勤.区间数决策集对分析[M].北京：科学出版社，2014：46-48.

[16]王欣，岳毅蒙.基于多元联系数集对分析的医疗设备供应商评价[J].甘肃科学学报，2019，31（5）：41-44.

[17]叶飞，李韬伟，杨琳，等.基于集对分析的职业健康风险评估应用[J].职业与健康，2019，35（13）：1742-1746.

[18]王亚鹏，王运斗，李雅平，等.基于集对势的卫生装备效能评估与优化方法[J].兵工自动化，2016，35（12）：60-63，71.

[19]覃杰，赵克勤.联系数在医院医疗质量发展趋势分析中的应用[J].中国卫生统计，2006，23（6）：502-504.

[20]覃杰，赵克勤.四元联系数态势排序在疗效整体评价中的应用[J].数理医药学杂志，2006，19（4）：419-421.

[21]覃杰，赵克勤.基于联系数的医院综合评价加权求和模型失效机理剖析与对策[J].中国医院统计，2006，13（1）：4-7.

（2019-03-04收稿 责任编辑：杨觉雄）

基金项目：国家重点研发计划“中医药现代化研究”重点专项（2018YFC1705301）;国家自然科学基金项目（81973860，81904214，81874470）;中华中医药学会2017-2019年度青年人才托举工程项目（QNRC2-B05）;上海市卫健委项目[ZY（2018-2020）-FWTX-1008，-4010，-CCCX-2004-08];上海科学技术委员会项目（18401932300）;上海人才发展基金（2017047）;上海市临床重点专科建设项目—中医皮肤病科（shslczdzk05001）;上海中医药大学预算内项目（18LK049）;研究生创新培养项目（Y2019027）

作者简介：卢怡（1992.06—），女，硕士，硕士研究生，研究方向：中医药防治皮肤病，E-mail：18621831967@163.com

通信作者：李斌（1968.08—），男，博士，主任医师，研究方向：中医药防治皮肤病，E-mail：18930568129@163.com