基于比值线性化的高适应性光栅细分方法研究

赵国博, 叶国永, 史永胜, 尹 磊, 刘红忠

(西安交通大学 机械工程学院,陕西 西安 710049)

1 引 言

光栅位移传感器因其良好的环境适应性、紧凑的系统结构、较低的价格成本等优势,已成为超精密工程中颇具活力和备受关注的跨尺度纳米测量技术[1～4]。电子细分是基于对光栅系统的正弦电信号的内插,是微米级栅距的反射式光栅实现亚微米级精度、纳米级分辨率测量的有效途径。近年来,随着电子技术和细分方法的发展,细分技术日益成熟,理论上已可实现最高达16 380倍的细分。在细分倍数低于100倍的细分方法中,应用比较广泛的主要有移相电阻链细分法和矢量运算法;在高倍细分方法中,应用比较广泛的主要有闭环跟踪细分法[5～8]、反正切细分法[9～12]、幅值线性化细分法[13～17]等。细分倍数、细分精度和适应性是评价电子细分方法性能的主要指标。细分误差是指一个栅距内细分间隔的不均匀性误差,其作为信号周期内误差,在早期的研究中一直没有给予足够的重视。随着反射式光栅测量系统向亚微米级精度迈进,细分误差在测量误差中的比重已不容忽略,且细分误差是非线性误差,难以补偿,已成为制约反射式光栅测量系统实现亚微米级精度、纳米级分辨率测量的关键因素,是国内外高精度光栅测量系统设计中面临的共同难题。

细分误差是由细分方法和信号质量决定。实际应用中,有效电子细分倍数受光栅信号质量的限制,不考虑细分误差而一味地提高电子细分倍数是没有实际意义的[18]。为减小细分误差,目前常规方法是通过电信号的实时修正来改善信号质量[19～22]。在这些信号修正方法中,以Heydemann椭圆[21]修正算法应用最广。信号实时修正原理,是通过计算前几个周期信号的特征参数来对后面的信号进行修正。在小步距测量等场合,会由于信号特征参数不足而无法进行信号修正,且修正误差不可避免。针对反射式光栅测量系统,由其敞开式机械结构决定,反射式光栅表面易受灰尘、油污等污染,读数头与反射式光栅之间的位姿亦会产生随机的微小波动,这均会引起光栅信号的随机波动,此种情况下的光栅信号随机波动亦难以通过信号实时修正电路进行完美修正。

从另外一个角度考虑,提高细分方法对非理想光栅信号的适应性,是减小细分误差的另一条途径。因此,设计新型的电子细分方法,使其在可以实现高倍细分的前提下,对非理想光栅信号具有可靠的调整功能和良好的适应性,是实现亚微米级精度、纳米级分辨率反射式光栅测量系统设计的关键技术。

2 线性化细分原理

结合反正切细分法和信号线性化细分法的优点,本文提出一种对非理想光栅信号具有良好适应性的高精度电子细分新方法。所提细分方法的原理如图1所示,其对光栅信号的处理过程主要包括:对光栅正余弦信号VS(θ)和VC(θ)进行预线性化处理,将高度非线性的正、余弦信号转换为近似三角波信号V1(θ);构建实时补偿信号,对近似三角波信号V1(θ)进行补偿,得到近似理想三角波信号V1-n(θ);对近似理想三角波信号V1-n(θ)进行辨向、细分运算。

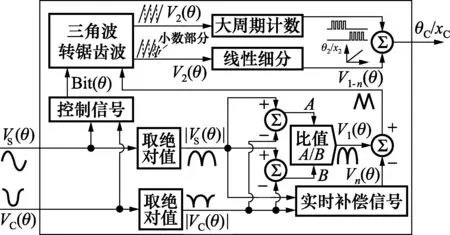
图1 所提方法的基本原理Fig.1 Basic principle of proposed scheme

2.1 正弦信号的预线性化方法

如图1所示,通过对原始信号VS(θ)、VC(θ)进行求绝对值和比值运算,可得到初步线性信号V1(θ):

(1)

式(1)表明,由于V1(θ)是基于比值运算,其波形不受VS(θ)和VC(θ)幅值波动的影响。如图2所示,V1(θ)为近似三角波信号,因此可以利用其幅值来线性计算位移。

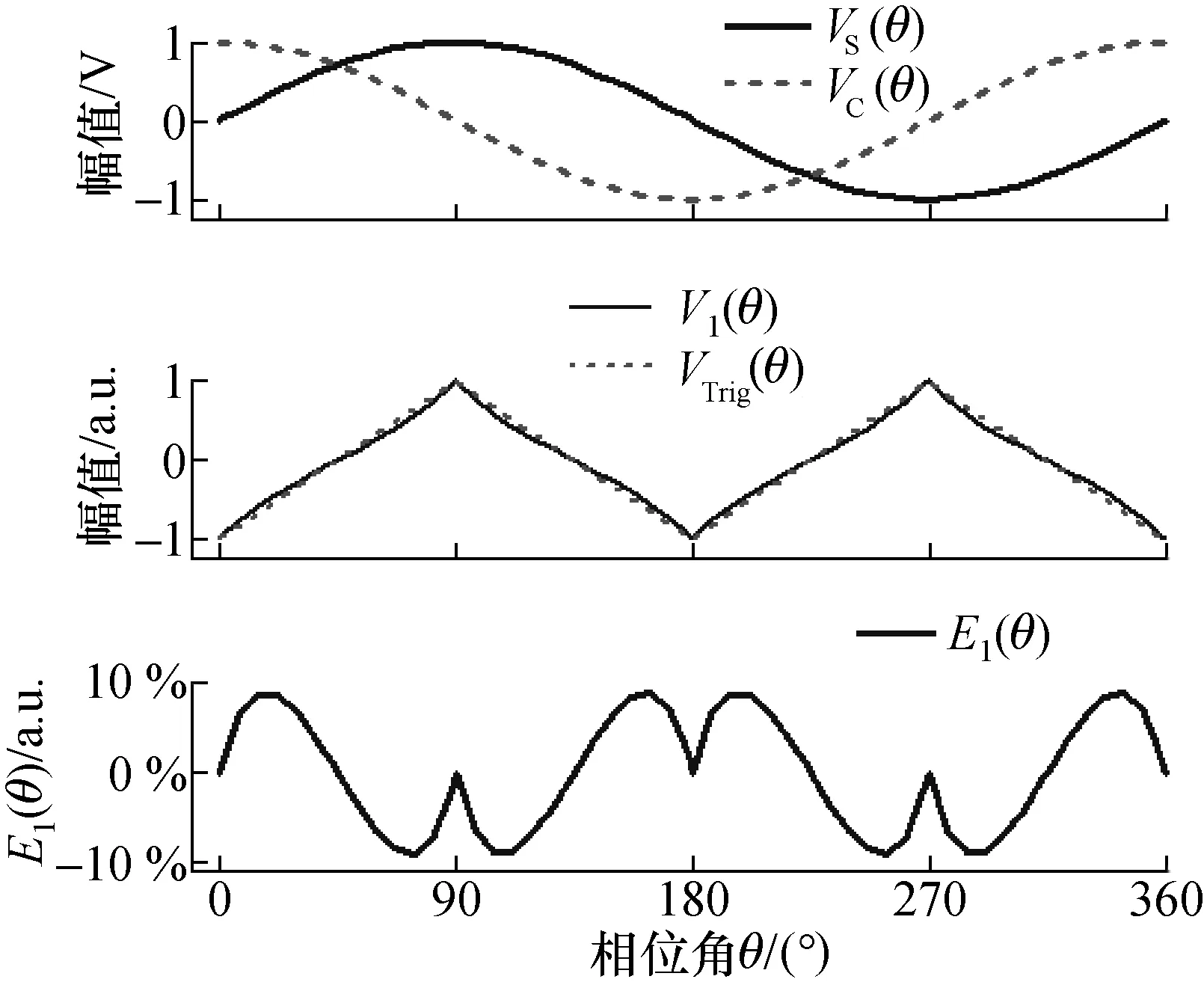
图2 V1(θ)与VTrig(θ)之间的波形偏差Fig.2 Waveform deviation between V1(θ) and VTrig(θ)

V1(θ)的线性度决定了位移计算的非线性误差。理想三角波的表达式为:

(2)

V1(θ)与VTrig(θ)之间的波形偏差为:

E1(θ)=V1(θ)-VTrig(θ)

(3)

由图2可得,偏差E1(θ)为周期函数且最大偏差max[E1(θ)]=9.05%。

2.2 实时补偿信号的构建

为了进一步减小位移计算时的非线性误差,需构造一实时补偿信号来进一步提高V1(θ)的线性度。实时补偿信号波形应与E1(θ)相同。因此,首先应分析E1(θ)的波形特征。由图2可知,E1(θ)具有以下特征:(a)周期为 π ;(b)周期内关于对称轴对称;(c)具有零点θ=nπ /4,其中n为整数。此外,为满足补偿信号的实时性,补偿信号应由光栅信号VS(θ)和VC(θ)来构造。经分析,|VS(θ)|×|VC(θ)|满足条件(a)和(b),然而只有零点θ=(2n) π/4;而|VS(θ)|-|VC(θ)|具有零点θ=(2n+1)π/4。因此,|VS(θ)|×|VC(θ)|×(|VS(θ)|-|VC(θ)|)和|VS(θ)|×|VC(θ)|×V1(θ) 都可满足补偿信号的条件(a)～(c),二者之间的差别在于后者含有分母|VS(θ)|+|VC(θ)|。因此,补偿信号的一般表达式可以写为:

Cn(θ)=kn×

(4)

式中:kn为系数;n为整数,n=0,1,2,3。

式(4)中需要确定的参数为n和kn,其中n决定Cn(θ)的形状,kn决定Cn(θ)的幅值。

补偿后的信号V1-n(θ)为:

V1-n(θ)=V1(θ)-Cn(θ)

(5)

V1-n(θ)与理想三角波函数VTrig(θ)之间的波形偏差为:

E1-n(θ)=V1-n(θ)-VTrig(θ)=

E1(θ)-Cn(θ)

(6)

式(6)表明,为了使V1-n(θ)的波形更加接近理想三角波,应使补偿信号Cn(θ)的波形接近E1(θ)。显而易见,波形形状相近是Cn(θ)与E1(θ)波形相近的前提。基于此认识,首先确定n值,使Cn(θ)的形状尽量接近E1(θ)形状;再确定kn值,使Cn(θ)的幅值接近E1(θ)的幅值。因此,计算归一化的E1(θ)与归一化的Cn(θ)之间的偏差,以忽略kn值的影响:

E1-n,N(θ)=norm[E1(θ)]-norm[Cn(θ)]

(7)

如图3所示,n=2时,E1-2,N的值最小,即C2(θ)与E1(θ)的波形形状最相近;n=3时,偏差E1-3,N的值虽然大于E1-2,N,但由式(4)可知n=3时,补偿信号C3(θ)不受光栅信号VS(θ)和VC(θ)幅值波动的影响。因此,相比之下,C2(θ)的补偿精度最高,而C3(θ)的对光栅信号幅值波动的适应性较好,各有其优势。

图3 不同n值下E1-n,N的波形Fig.3 Waveform of E1-n,N under different values of n

2.2.1 实时补偿信号C2(θ)的构建及补偿效果

实时补偿信号C2(θ)的参数k2的值可由式(6)确定,偏差E1-2(θ)的最大值为k2的函数。如图4所示,当k2=-0.757 9时,E1-2(θ)取得最小值且此时max[E1-2(θ)]=0.12%。此时,补偿后的信号V1-2(θ)为:

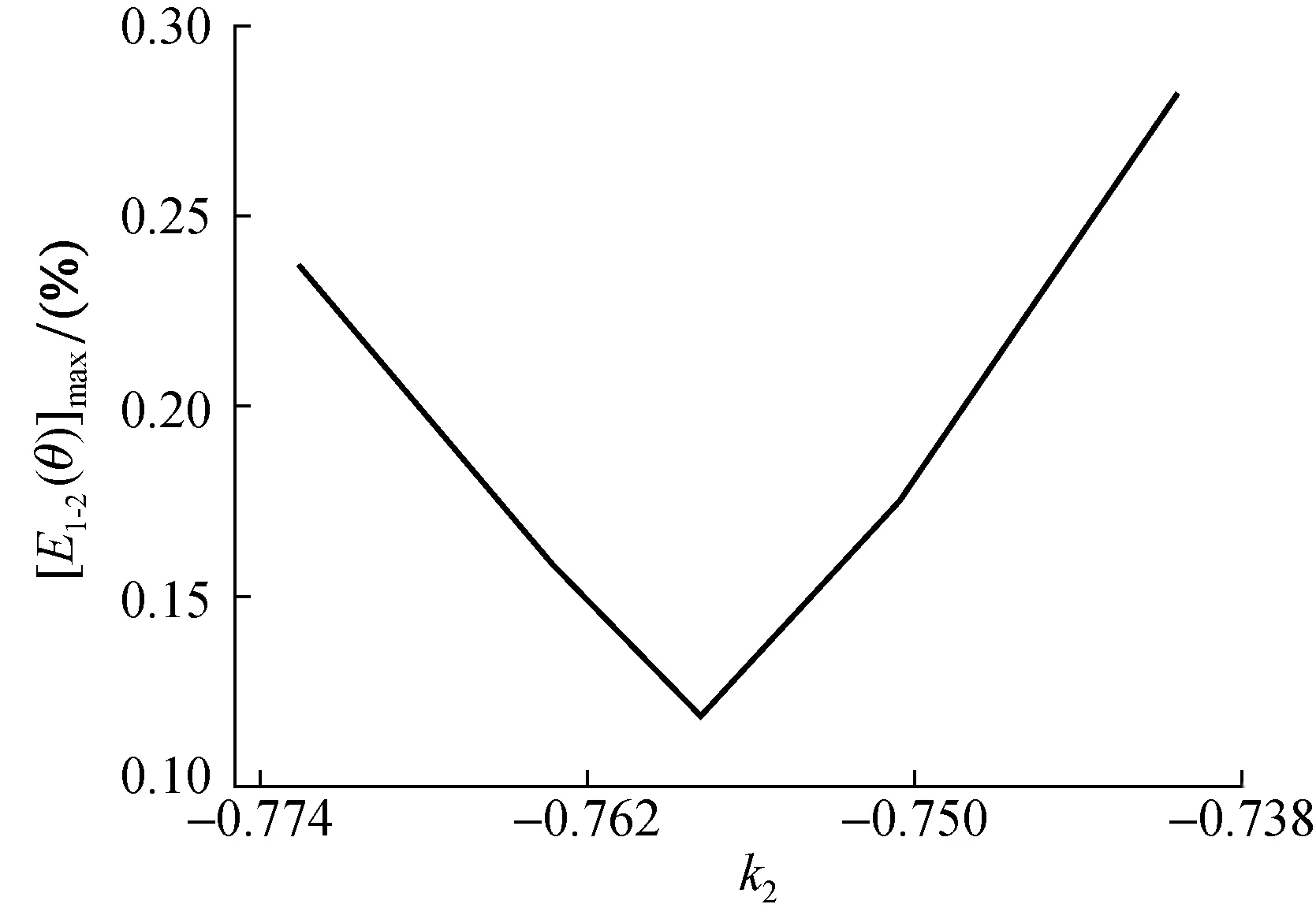
图4 E1-2(θ)的最大值与k2的关系Fig.4 The relationship between the maximum value of E1-2(θ) and k2

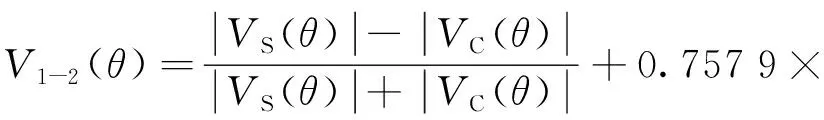
(8)

V1-2(θ)与理想三角波函数VTrig(θ)之间的波形偏差E1-2(θ)的波形如图5所示。相比于图2,补偿信号C2(θ)使得输出信号的线性度得到明显改善,V1-2(θ)与理想三角波信号VTrig(θ)的偏差小于0.12%。

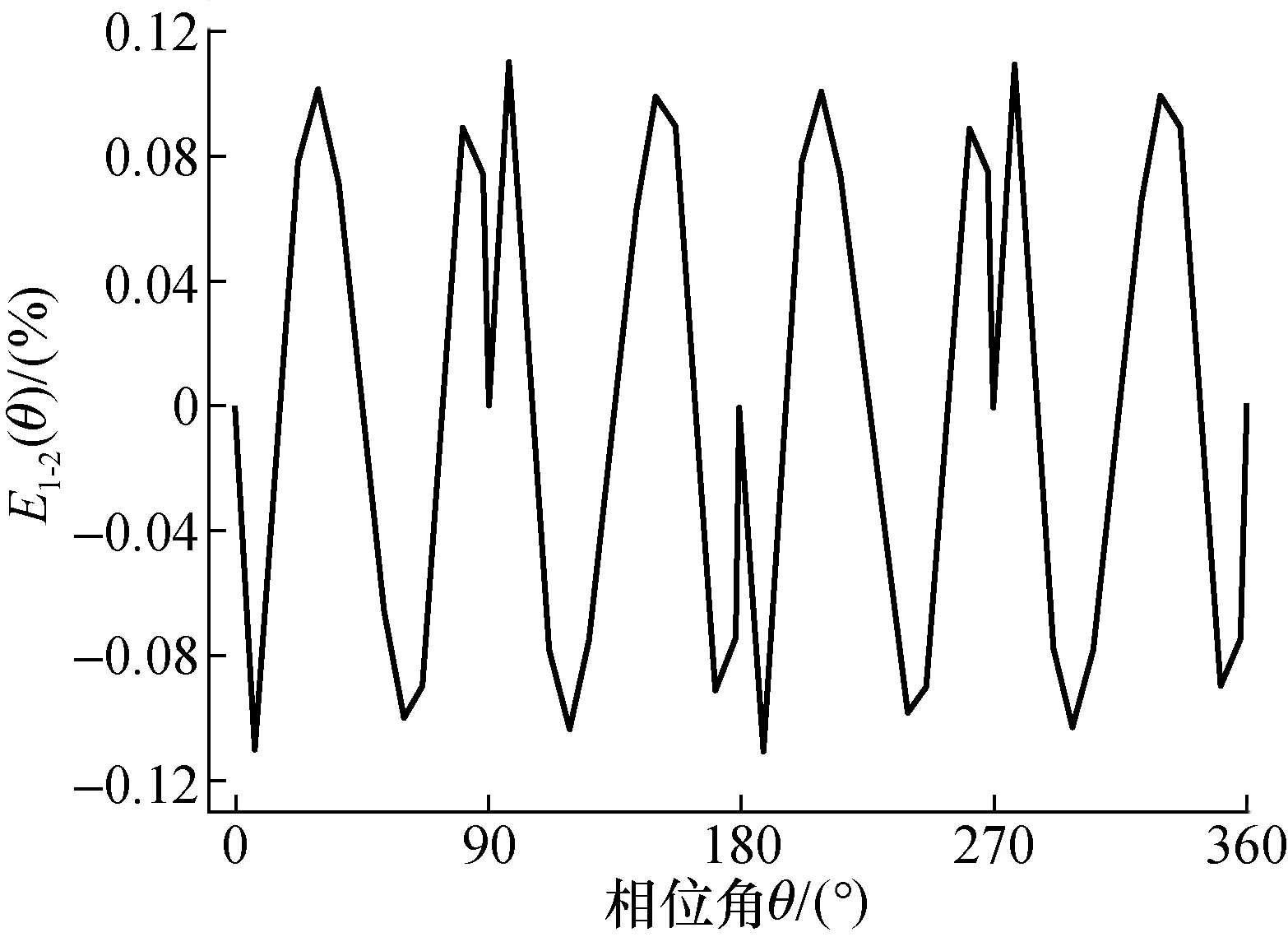
图5 V1-2(θ)与VTrig(θ)之间的偏差Fig.5 Deviation between V1-2(θ) and VTrig(θ)

相对于补偿信号C2(θ),虽然补偿C3(θ)精度相对较低,但其不受光栅信号幅值波动的影响。特别适用于工况较差、信号幅值波动较大的场合。k3的值与E1-3(θ)的关系如图6所示,当k3取值-0.927时,E1-3(θ)取得最小值且此时max[E1-3(θ)]=0.78%。此时,补偿后的信号V1-3(θ)为:

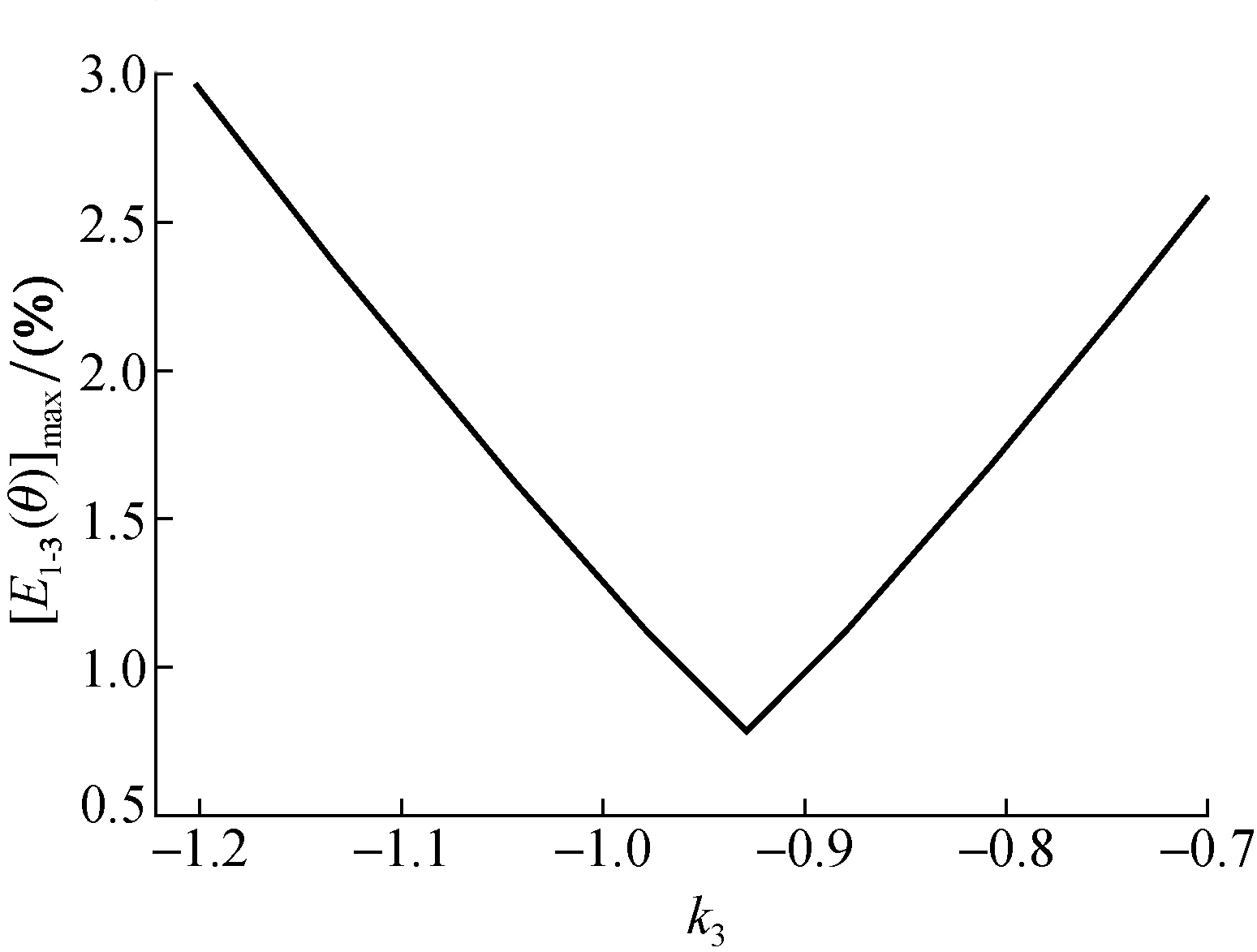
图6 E1-3(θ)的最大值与k3的关系Fig.6 The relationship between the maximum value of E1-3(θ) and k3

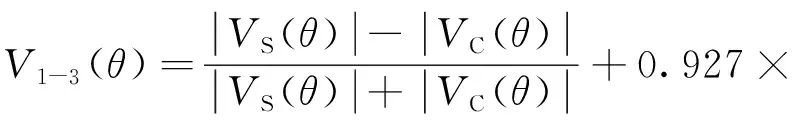
(9)

V1-3(θ)与理想三角波函数VTrig(θ)之间的波形偏差E1-3(θ)的波形如图7所示,V1-3(θ)与理想三角波信号VTrig(θ)的偏差小于0.78%。

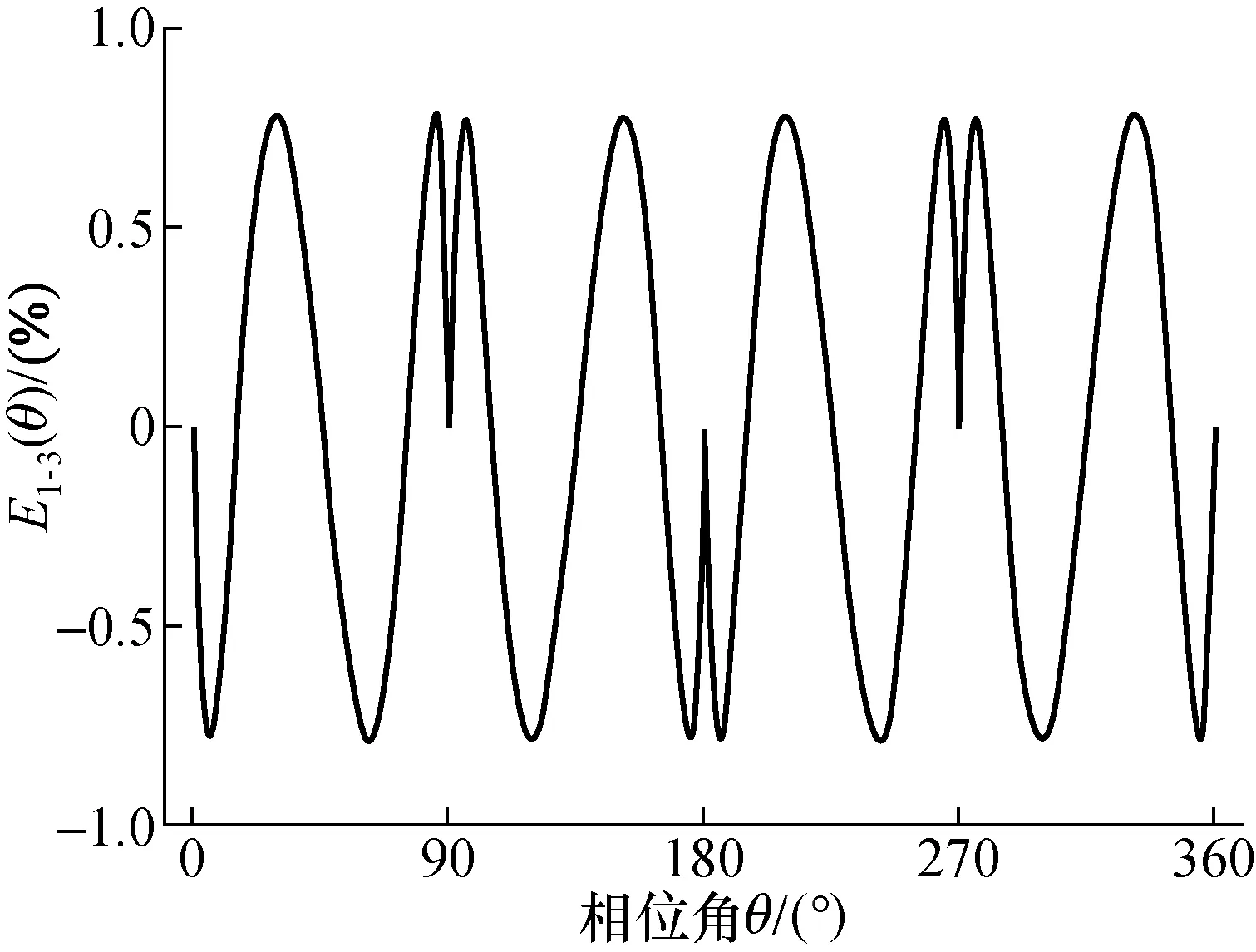
图7 V1-3(θ)与VTrig(θ)之间的偏差Fig.7 Deviation between V1-3(θ) and VTrig(θ)

2.3 细分及辨向计数原理

为了辨别读数头相对光栅尺的运动方向,引入鉴向信号Bit(θ),其表达式为:

Bit(θ)=fS(θ)⊕fC(θ)

(10)

式中:fi(θ)为判别光栅信号Vi(θ)正负产生的控制信号。其定义如下:

(11)

在鉴向信号Bit(θ)的控制下,近似理想三角波信号V1-2(θ)或V1-3(θ)转换为带有方向信息的锯齿波信号V2(θ):

(12)

图8所示为光栅正反向运动时,V2(θ)和Bit(θ)的波形图。正向运动时,V1-n(θ)转换为具有正斜率的锯齿波;反向运动时,V1-n(θ)转换为具有负斜率的锯齿波。

“非遗”传承保护的关键因素是人的因素，这是物质文化遗产与“非遗”传承保护的根本区别所在。就“非遗”而言，人在技在，人亡技亡，培养“人才”与“非遗”传承保护同等重要。江苏既要加大“非遗”传承人的培养力度，提高他们传承“非遗”的尊严感和幸福感，又要加强“非遗”管理人才的培养，指导他们用专业的思路、专业的眼光、专业的技能从事“非遗”管理工作。“非遗”人才培养要注重理论和实践相结合，注重国际交流与国内研讨相结合，注重高校培养和专业培训相结合，以先进的文化理论培养适应新时代江苏文化发展的专业化“非遗”传承保护人才。

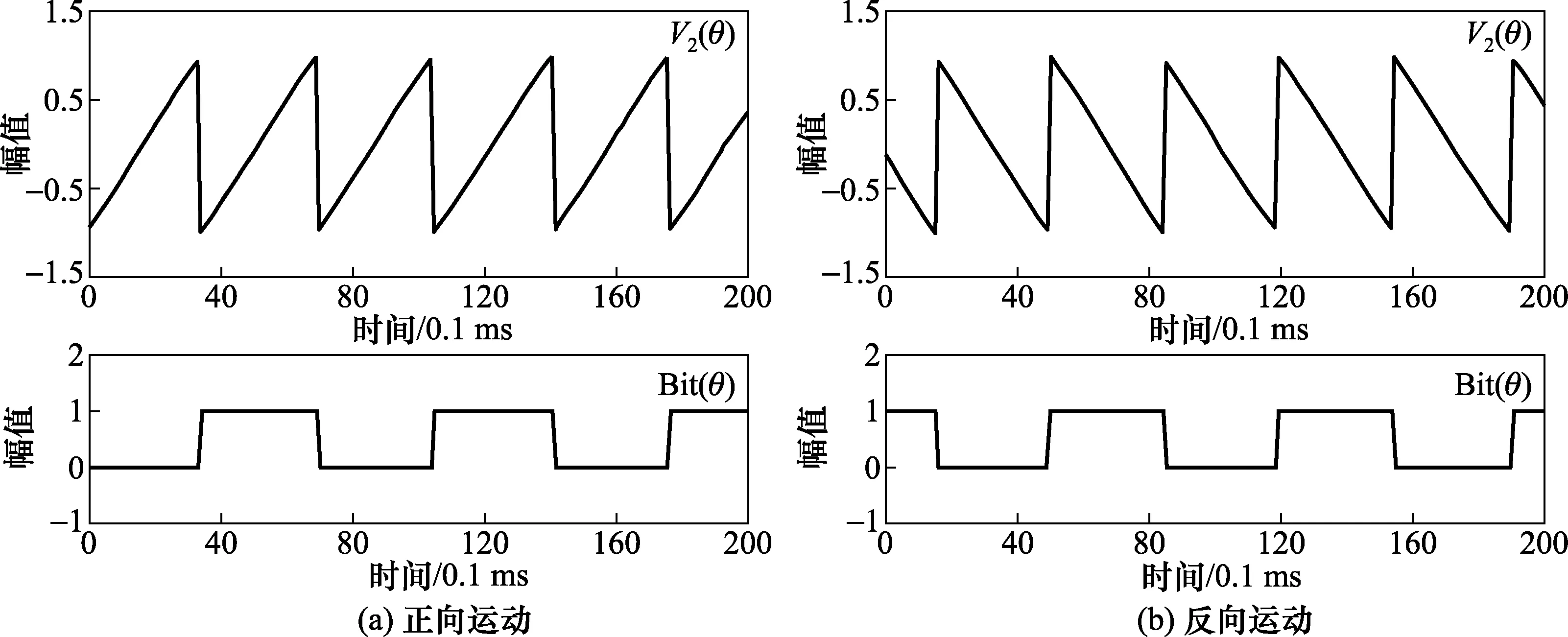
图8 光栅正反向运动时V2(θ)和Bit(θ)的波形图Fig.8 Waveforms of V2(θ) and Bit(θ) when the grating is moving in forward and reverse directions

对于大于p/4(p为光栅尺栅距)的位移,采用整周期计数的方法计算位移。如图9所示,当正向运动且在V2(θ)的下降沿处,生成正向计数脉冲UP, 当反向运动且在V2(θ)的上升沿处,生成反向计数脉冲DOWN。

图9 整周期计数原理Fig.9 Principle of period counting

由于V2(θ)的幅值与位移值呈线性关系,小于p/4的位移可以线性计算为:

(13)

式(13)表明,可以通过对V2(θ)的幅值细分来提高θ2的分辨率;θ2的分辨率取决于V2(θ)的幅值分辨率,即细分倍数取决于A/D转换器位数。采用12位的A/D转换器(AD9 226),针对20 μm栅距的反射式光栅测量系统,理论上分辨率优于1 nm;然而受噪声及信号质量所限,一味地提高细分倍数并无太大实际意义,实际应用中分辨率取为10 nm。最终,角位移θC计算为:

(14)

式中:NU为正向计数脉冲个数/个;ND为反向计数脉冲个数/个。

对应的位移xC为:

(15)

3 细分精度及适应性分析

3.1 细分方法的理论细分精度

由于V1-n(θ)并非完美的三角波信号,其与标准三角波VTrig(θ)的偏差如图5和图7所示,当利用式(13)来线性计算位移时,会产生非线性误差。利用V1-2(θ)来计算位移时,理论细分精度如图10(a)所示,最大细分误差为0.053°,针对20 μm的反射式光栅测量系统,对应的细分误差为0.003 μm;当利用V1-3(θ)来计算位移时,理论精度如图10(b)所示,最大误差为0.352 8°,针对20 μm的反射式光栅测量系统,对应的细分误差为0.019 6 μm。

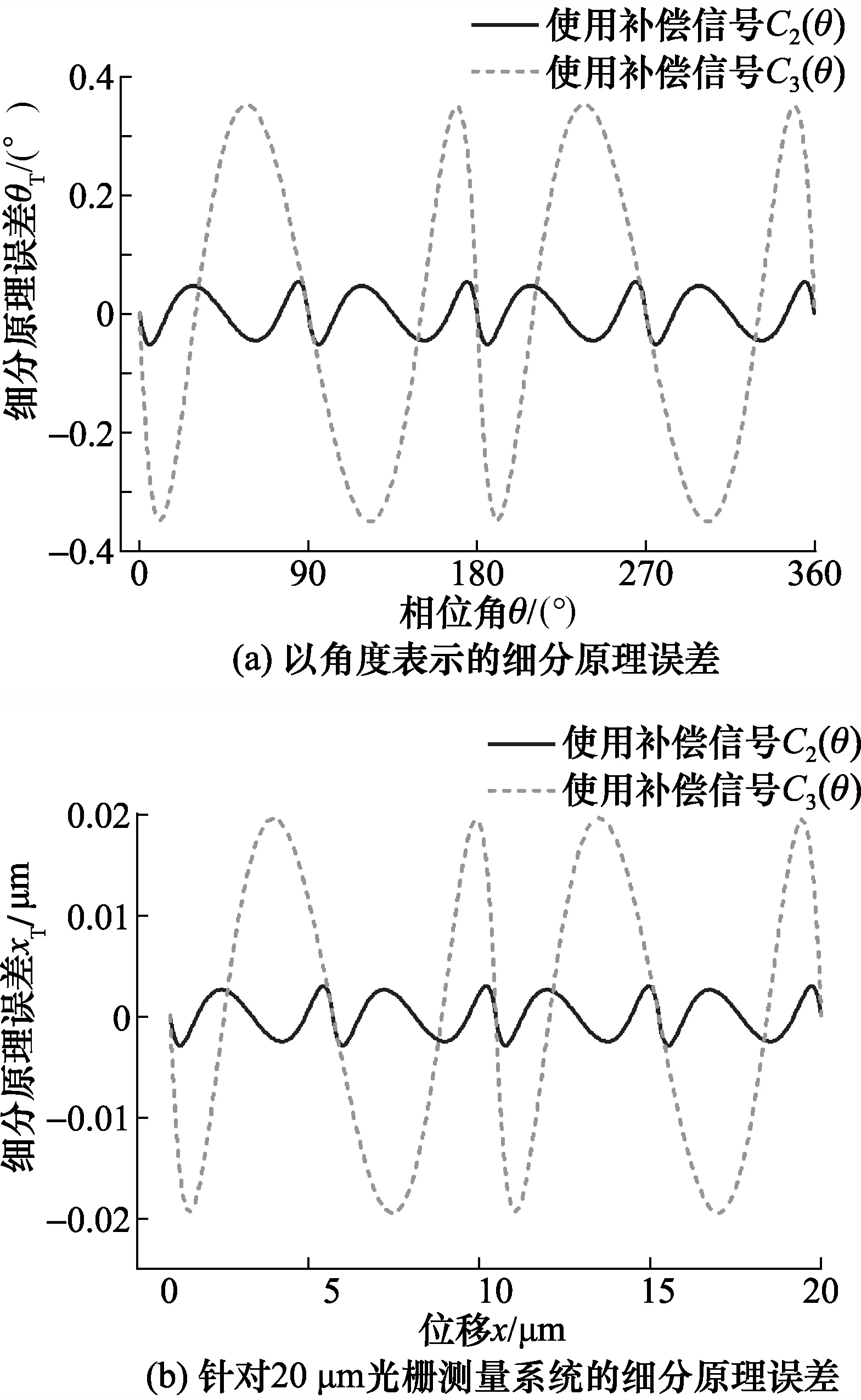
图10 所提细分方法的细分原理误差Fig.10 Principle error of the proposed method

3.2 细分方法对非理想信号的适应性分析

细分方法的适应性是指细分误差对非理想光栅信号的敏感程度。实际应用中,受各种因素的影响,光栅信号主要表现为以下5种误差形式:幅值波动、幅值不等、直流偏置、相位不正交误差和高次谐波失真。实际光栅信号可以表示为:

(16)

式中:A1、A2为信号幅值,V;F1、F2为表征信号波形的函数,min(Fα) = -1,max(Fα) = 1;θ为与光栅位移x成正比的电信号相位角,rad;φ1、φ2为信号初始相位角,rad;B1、B2为信号直流偏置,V。

A3sin (3θ)+ΔB

(17)

式中:β为信号幅值波动系数;ΔA1为信号幅值的偏离量,V;Δφ为信号相位偏离量,rad;A3为3次谐波信号的幅值,V;ΔB为信号直流偏置量,V。

将式(17)所表达的非理想光栅信号代入式(8)或式(9)得到线性化信号,再代入式(14)即可得位移值θC。光栅信号各参量的偏离值g引入的细分误差为:

eg(θ)=θC-θ-θT

(18)

式中:θ为实际位移值,rad;θT为细分方法的理论误差值,rad。

为了评估所提细分方法对非理想光栅信号的适应性,在非理想光栅信号情况下,将所提细分方法的细分误差,与反正切细分方法、绝对值加减法的细分方法进行对比。针对20μm的反射式光栅测量系统,细分误差的对比结果如图11所示。

图11 细分方法对非理想光栅信号的适应性的对比Fig.11 Comparison of the adaptability of subdivision methods to non-ideal grating signals

图11表明,在相同信号误差含量下,正余弦相减法对信号幅值波动和幅值不等误差比较敏感;反正切细分法对信号直流偏置、相位偏离及高次谐波比较敏感。相比之下,本文所提细分方法对信号的这五项误差都具有较高的抗干扰能力,因此工况条件下的适应性更强。进一步比较所提细分方法使用补偿信号C2(θ)和C3(θ)时的细分误差,亦会发现:当使用补偿信号C3(θ)时,虽然细分误差稍大,但抗干扰性强,因此适用于要求高精度、工作环境较差的环境;当使用补偿信号C2(θ)时,虽然抗干扰性稍差,但细分原理误差接近于0,因此适用于要求超高精度、工作环境适中的场合。

4 性能测试实验

4.1 细分方法的软硬件实现

实验采用12位模数转换器AD9226芯片将光栅信号VS(θ)和VC(θ)转化为数字信号。为提高所提细分方法的实时性,采用FPGA实现所提细分方法的线性化、实时补偿信号构建、辨向、计数和细分运算,得到位移值xC。所选用FPGA型号为Altera 公司的Cyclone Ⅳ系列的EP4CE30F23C8N,所使用开发软件为QuartusⅡ 13.1,所使用开发语言为Verilog 硬件描述语言。

4.2 实验结果

测试实验中,采用实验室现有高精度一维测量机实验台作为光栅测量系统的支撑平台。采用Renishaw公司的XL-80激光干涉仪作为测量基准,对光栅测量系统进行误差标定。实验中,所用光栅尺为20 μm栅距的钢带光栅。细分误差测试如图12(a)所示,采用压电驱动器(MTp-200/30, Core Tomorrow Co, China)产生微小步距位移,其最大输出位移量为30 μm,产生的最大驱动力为1 800 N。压电驱动定位平台,其主要参数为:实测位移放大倍数为1.943倍;整个压电驱动平台的实测量程为48 μm,实测运动步距/分辨率为3 nm。20 μm栅距的钢带光栅通过其背胶粘于压电驱动定位平台,随压电驱动定位平台移动。

测试结果如图12(b)和12(c)所示,当使用实时补偿信号C2(θ)时,所提细分方法的细分误差小于0.08 μm;当使用实时补偿信号C3(θ)时,所提细分方法的细分误差小于0.25 μm。

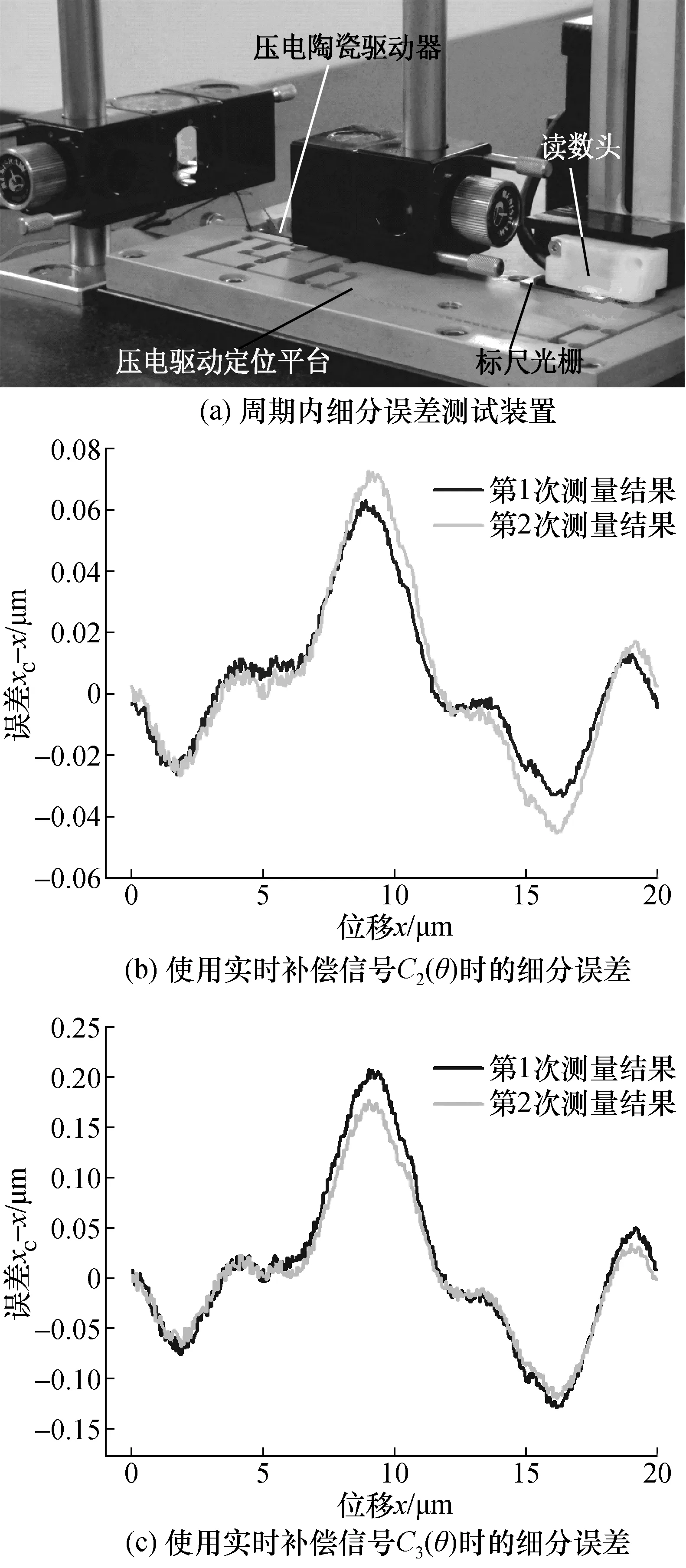
图12 周期内细分误差测量实验装置与结果Fig.12 Experiment setup and results of error measurement in a period

5 结 论

针对信号实时修正方法在小步距测量和一些复杂工况环境下的局限性,从提高细分方法对非理想光栅信号的适应性的角度出发,提出了基于比值法和信号线性化法相结合的新型电子细分方法,构建了2种实时补偿信号以进一步提高信号的线性度;详细阐述了所提细分方法的细分原理,分析了其在非理想光栅信号输入情况下的细分误差;设计了基于高速AD和FPGA的细分计数模块,实现了对光栅信号的2 000倍电子细分。通过实验对所提细分方法的细分精度和适应性进行了测试,最终得出以下结论:

(1)所提细分方法对非理想光栅信号的适应性明显优于常用的反正切细分法和正余弦绝对值相减细分法;(2)针对20 μm栅距的光栅测量系统,根据所使用的实时补偿信号的不同,所提细分方法的理论细分误差分别为0.003 μm和0.019 6 μm;(3)实际光栅信号输入情况下,根据所使用的实时补偿信号的不同,所设计的细分计数模块的细分误差分别为0.08 μm和0.25 μm。