高一数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分.在每小题的四个选项中，只有一项是符合题目要求的)

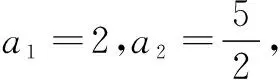
(A)49 (B)50 (C)51 (D)52

2.若直线l∥平面α，直线a⊂α，则l与a的位置关系是( )

(A)l∥a(B)l与a异面

(C)l与a相交 (D)l与a没有公共点

3.等比数列{an}的前n项和为Sn,已知S3=a2+10a1,a5=9,则a1=( )

4.若a,b为异面直线，a⊂α,b⊂β,α∩β=l，则( )

(A)l与a,b分别相交

(B)l至少与a,b中的一条相交

(C)l与a,b都不相交

(D)l至多与a,b中一条相交

(A)120° (B)90° (C)60° (D)45°

6.在数列{an}中,已知Sn=1-4+7-10+13-16+…+(-1)n-1(3n-2),则S15+S22-S31的值( )

(A)57 (B)46 (C)13 (D)-57

7.如图,在∆ABC中,∠ACB=90°，直线l过点A且垂直于平面ABC,动点P∈l，当点P逐渐远离点A时,∠PCB的大小 ( )

(A)不变 (B)变小

(C)变大 (D)有时变大有时变小

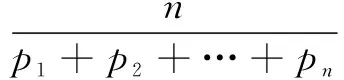
二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题的四个选项中,有多项符合题目要求．全部选对得5分,部分选对得3分,有选错的得0分)

9.已知α,β是两个平面,m,n是两条直线,有下列四个结论,正确的是( )

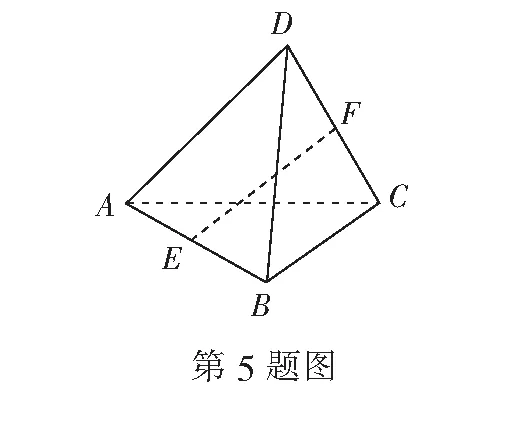
(A)如果m∥α,m∥n,那么n∥α

(B)如果m⊥α,n∥α,那么m⊥n

(C)若直线m垂直于平面α内的任意一条直线,则m⊥α

(D)如果m⊥α,n⊥α,那么m∥n

10.定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an}，数列{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(-∞,0)∪(0,+∞)上的四个函数中,是“保等比数列函数”的为( )

(A)f(x)=x2(B)f(x)=2x

11.已知数列{an}不是常数列,其前n项和为Sn,则下列选项正确的是( )

(A)若数列{an}为等差数列,Sn>0恒成立,则{an}为递增数列

(B)若数列{an}为等差数列,a1>0,S3=S10,则Sn的最大值在n=6或7时取得

(C)若数列{an}为等比数列,则S2 021a2 021>0恒成立

(D)若数列{an}为等比数列,则{2an}也为等比数列

12.正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点,则( )

(A)直线D1D与直线AF平行

(B)直线A1G与平面AEF平行

(D) 点C与点G到平面AEF的距离相等

三、填空题(本大题共4小题,每小题5分,计20分)

13.等差数列{an}中,已知前15项的和S15=90,则a8=______.

14.已知面α∥面β,点P是面α,β外一点(如图所示),且直线PAB,PCD分别与α,β相交于点A,B,C,D,若PA=4,PB=5,PC=3,则PD=______.

15.下列结论中,正确的序号是______.

① 如果一个平面内有两条直线平行于另一个平面,那么这两个平面平行;

② 如果一个平面内有无数条直线平行于另一个平面,那么这两个平面平行;

③ 如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行;

④ 如果一个平面内的一个角(锐角或钝角)的两边分别平行于另一个平面内的一个角的两边,那么这两个平面平行.

四、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)四棱锥P-ABCD中,PA⊥底面正方形ABCD,且PA=AB=a,,E,F是侧棱PD,PC的中点,

(1)求证:EF∥平面PAB;

(2)求直线PC与底面ABCD所成角θ的正切值.

18.(本小题满分12分)已知等差数列{an}的前n项和为Sn,满足a6+a8=-10，S10=-35.

(1)求数列{an}的通项公式;

19.(本小题满分12分)如图,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.

(1)求证:MN⊥CD;

(2)若∠PDA=45°,求证:MN⊥平面PCD.

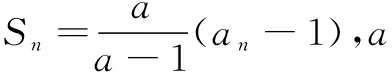
(1)求数列{an}的通项公式;

21.(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,B1C⊥AB,侧面BCC1B1为菱形.

(1)求证:B1C⊥平面ABC1；

(2)如果点D,E分别为A1C1,BB1的中点,求证:DE∥平面ABC1.

22.(本小题满分12分)已知{an}是以a为首项,q为公比的等比数列,Sn为它的前n项和.

(1)当S1,S3,S4成等差数列时,求q的值;

(2)当Sm,Sn,Sl成等差数列时,求证:对任意自然数k,am+k,an+k,al+k也成等差数列.

参考答案

一、单项选择题

1.D；2.D;3.C;4.B;5.C;

6.D;7.A;8.C.

二、多项选择题

9.BCD；10.AC;11.BC;12.BC.

三、填空题

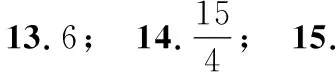
四、解答题

17.(1)∵EF是∆PCD的中位线,∴EF∥CD；又CD∥AB,∴EF∥AB.

又AB⊂面PAB,∴EF∥面PAB.

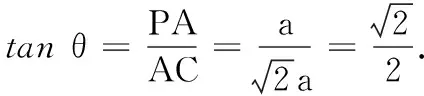
18.(1)依题意，有

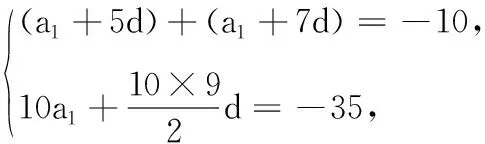
故an=2-n.

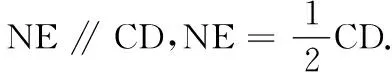
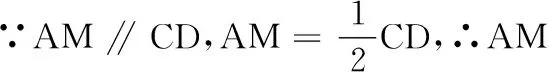
∵PA⊥平面ABCD,CD⊂平面ABCD,∴CD⊥PA.又∵CD⊥AD,PA∩AD=A,∴CD⊥平面ADP.

∵AE⊂平面ADP,∴CD⊥AE,∴MN⊥CD.

(2)当∠PDA=45°时,Rt∆PAD为等腰直角三角形,则AE⊥PD.又MN∥AE,故MN⊥PD,PD∩CD=D.

由(1)知MN⊥CD,∴MN⊥平面PCD.

20.(1)由S1=a1,可得a1=a.

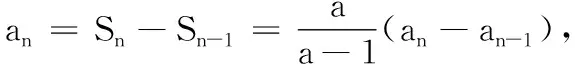
(2)由(1)及条件,易知

(*)

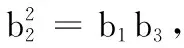
21.(1)因三棱柱ABC-A1B1C1的侧面BCC1B1为菱形,故B1C⊥BC1.

又B1C⊥AB,且AB,BC1为平面ABC1内的两条相交直线,故B1C⊥平面ABC1.

(2)如图,取AA1的中点F,连结DF,FE.

因D为A1C1的中点,故DF∥AC1,EF∥AB.

因DF⊄平面ABC1,AC1⊄平面ABC1,故DF∥面ABC1. 同理,EF∥面ABC1.

因DF,EF为平面DEF内的两条相交直线,故平面DEF∥面ABC1.因DE⊂平面DEF,故DE∥面ABC1.

(2)若q=1,则{an}的每项an=a,此时am+k,an+k,al+k显然成等差数列.