再谈三角形面积最值问题*

王 义 毛晓伟

(安徽省宿州市砀山中学，235300)

三角形面积问题是解三角形专题中的重要题型,尤其是有关三角形面积的最值题,极能考查学生综合解决问题的能力,备受命题者的青睐.本文从五种类型面积最值问题入手,举例说明解题的不同策略,并推广总结,以期抛砖引玉.

为叙述方便,在下列问题中按常规约定,a，b，c分别为∆ABC的内角A，B，C所对边长.

类型1已知一角及其对边,求三角形面积的最大值

例1在∆ABC中,已知(2a-c)cosB=bcosC.

(1)求角B的大小;

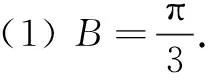
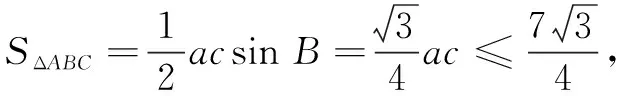
类似问题(2)的求解过程,不难得到如下推广形式.

类型2已知一角及邻边,求∆ABC面积的取值范围.

(1)求角B的大小;

(2)若∆ABC为锐角三角形,且c=1,求∆ABC面积的取值范围.

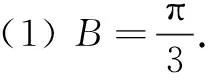
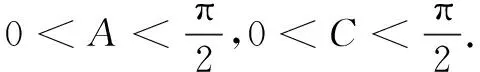
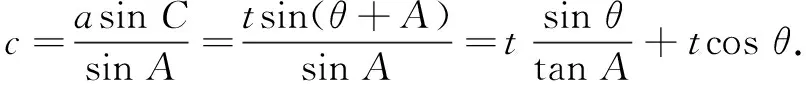
类型3已知一角及该角所对边的中线,求三角形面积的最大值

(1)求角C的大小;

(2)若D为AB的中点,且CD=1,求∆ABC面积的最大值.

完全类似地,推广到一般,可得

类型4已知一边及两边和,求三角形面积的最大值

例4在∆ABC中,已知2sinA=sinB+sinC,a=2,求∆ABC面积的最大值.

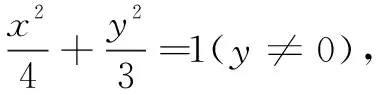
循此,推广到一般,可得

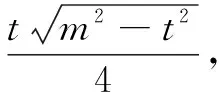
类型5已知一边及另两边之比,求三角形面积的最大值.

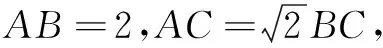
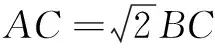
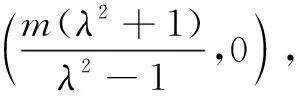
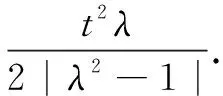
上述五种类型是求三角形面积最值的常见题型,其求解方法看似多种多样,但实质上各种解题方法也是相通的.具体说可从以下几个视角分析:(1)转角化边,利用正余弦定理及基本不等式求解;(2)转边化角,利用正余弦定理及三角函数求解;(3)建立适当的坐标系,利用坐标法求解;(4)转化为向量问题,利用向量求解;(5)几何思想,借助图形的几何性质求解.