关注生成 超越预设——对一道教材例题追问引发的思维探究

樊 蓉

(江苏省扬州中学，225002)

布鲁姆曾说:“没有预料不到的成果,教学也就不成为一种艺术了.”学生的创造力、想象力、差异性也会使课堂教学充满复杂性、丰富性和多变性.现行课程标准期望老师打破不折不扣按教学预设“照章办事”的观念,重视教学的生成.如果教师能够关注课堂生成,把握预设之外的“新情况”、“新事件”,在学生思维碰撞的过程中,创造生成性资源,就能让课堂变得灵动而富有生命力.笔者在课堂上讲解教材中一道例题时,就遇到了一次预设之外的“惊喜”,现与大家分享.

一、情境再现

题目(苏教版《数学》(必修5)第19页例4)如图1,半圆O的直径为2,C为直径AB延长线上的一点,OC=2,P为半圆上任意一点,以PC为一边作等边三角形PCD,问:点P在什么位置时,四边形OPDC的面积最大?

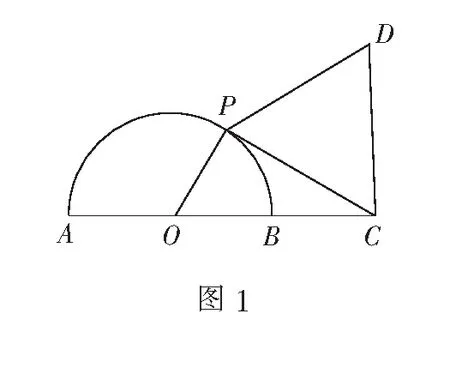
1. 达成既定性目标

此题是在学生已系统学习了正弦定理和余弦定理有关基本内容后,检查学生是否具备“边”与“角”的转化能力的典型应用例题.问题呈现后,笔者并没有急于引导学生解题,而是发挥学生在课堂的主体作用,先让他们自己动手做.

很快,大部分学生给出了答案.思路基本上都是先设∠POC=θ,利用余弦定理建立起PC关于θ的函数关系式,再利用S四边形POCD=S∆PCD+S∆POC,将四边形POCD的面积转化为关于θ函数,最后化简成求三角函数的最值问题.学生的解题思路和教材中的解题思路一致,教学既定目标已经达成.

2. 创设生成性资源

设定的教学目标虽已完成,笔者却意犹未尽,借此机会顺流而下.

师:(提问学生1)你为什么会想到将面积转化为关于∠POC的函数?

生1:面积的变化与点P的位置有关,而点P的位置与∠POC一一对应.

师:(追问)本题中还有什么量的变化与∠POC有关呢?

生2:(抢答)还有线段的长度.

师:那你觉得可以研究哪个线段的长度变化呢?

生2不假思索回答是线段PC.

笔者没有表态,这时旁边的学生3说道:“PC的变化范围一眼就看出来了,没有研究的意义.”

师:(追问生3)那你觉得哪些线段长度的变化更值得我们去研究呢?

生3:(想了一想)线段OD的长度变化.

师:为什么呢?

生3:点P位置的变化决定了点D的位置变化,那点D的位置一定与∠POC相关,由此想到研究OD长度的取值范围.

经历了上述师生互动,课堂气氛立刻活跃了起来.

笔者对全班同学抛出一个新的问题:“既然大家已经意识到线段OD的变化随∠POC的变化而变化,那就请大家尝试从不同的视角出发合理建模,探究一下OD长度的变化范围.”课堂迅速安静了下来,十分钟的思索后,精彩纷呈…

3. 展示精彩思维

课堂讨论中生成的问题获得许多有趣的求解思路.

思路1从解三角形角度建立模型

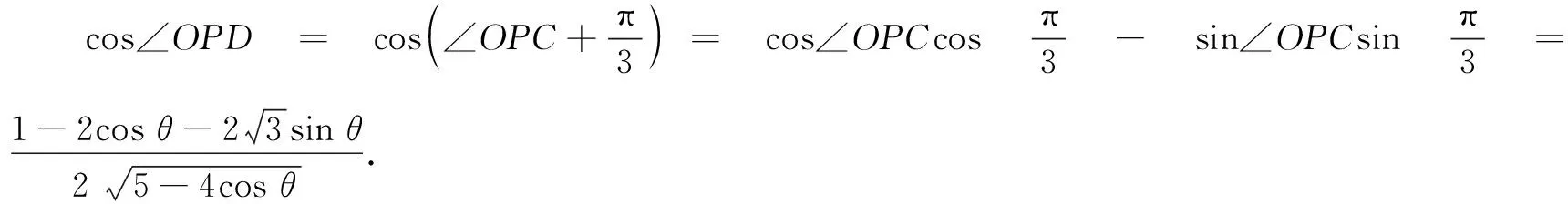
评注从现阶段学习的解三角形内容入手,利用正余弦定理解决问题,契合教材例题编写的出发点,属于常规方法.运用此法的同学已能对本章知识熟练进行运用.

思路2从解析几何角度建立模型

评注此解法利用坐标将问题进行代数化求解,对点D的坐标表示的处理具有一定的能力要求.

思路3从几何性质出发建立模型

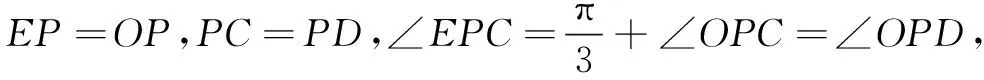
评注通过相似形简化运算,体现了数学化繁为简的真谛.运用此法的学生充分考虑了图象的几何特征,构思巧妙.

思路4从图象变换角度建立模型

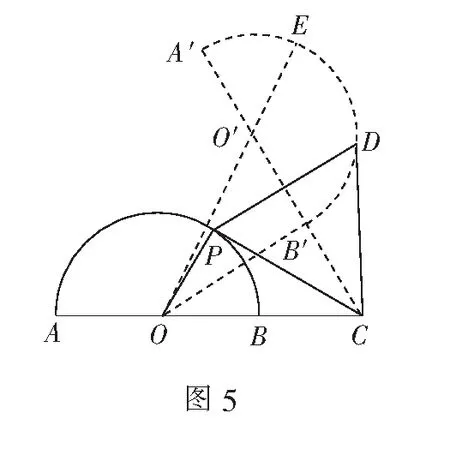
评注从图象变换的角度考虑问题,不仅让初中数学知识在高中阶段发挥威力,还能使学生用动态的眼光观察图形,达成直观想象能力的飞跃.

二、教学启示

教学预设能使课堂教学的开展有章可循；而教学生成,则使得课堂活动的开展充满惊喜.从本节课教学过程看,立足教材,利用教材中的例题,引导学生解决有价值的数学问题是笔者的预设.把握课堂教学的节奏,顺势而为引发的追问,是预设之外的生成.而被激活的学生思维,从不同角度进行建模、探究则是“意外的惊喜”.不同的解题思路恰好体现了学生对“数学知识”、“思想方法”的“再创造”；同时也反映出学生在数学建模、数学运算、直观想象、逻辑推理等数学核心素养能力的差别.

课堂教学的生成不可“预设”,也不可“预约”,它具有随机性和突发性.但老师备课时可以在课堂预设时适当“宏观”,扩大生成空间;课堂教学中适当关注生成,随机调整预设;教学反思时,研究预设与生成的协调改进措施.叶澜教授曾所说过:“课堂应是向未知方向挺进的旅程,随时都有可能发现意外的通道和美丽的图景，而不是一切都必须遵循固定而没有激情的行程.”作为一线教师应根据实际情况,把握课堂教学的自然生成,不拘泥于教材,大胆创新.