基于抗非线性SVM的几何整形可见光通信系统
2020-08-06牛文清贾俊连哈依那尔
迟 楠,牛文清,贾俊连,哈依那尔
复旦大学电磁波信息科学教育部重点实验室,上海200433
近年来,随着互联网时代多样化应用与终端用户数量的爆炸式增长,前所未有的数据量传输的需求成为通信系统性能提升面临的巨大挑战. 面对无线频谱资源日益紧张的现状,研究者们开始将目光聚焦于一种拓宽频谱资源的新兴通信方式——可见光通信(visible light communication, VLC)技术. 可见光通信将发光二极管(light emitting diode, LED)作为发射光源,在380~790 nm 的可见光波段传输,凭借其传输容量大、安全性高、绿色节能、抗电磁干扰等优点在未来移动通信室内接入和水下无线通信等方面显示出巨大潜力[1-3].
为了逼近可见光通信系统容量极限,通过重新设计高阶QAM 发射信号的星座点分布以最大化最小欧氏距离的几何整形(geometrically shaping, GS)技术得到了广泛研究[4-5]. 然而,由于可见光信道的特殊性,可见光通信系统的性能受到了线性和非线性效应的影响,尤其在复杂信道和高发射功率的情况下,非线性效应将成为限制系统性能的主要因素[6],它会使信号产生严重的失真现象. 对于QAM 信号来说,表现为星座点的移位和变形. 在这种情况下,传统的基于欧氏距离的星座点分类判决方法的误码率会大大增加,以致严重恶化系统性能.
支持向量机(support vector machine, SVM)作为一种经典的有监督的机器学习算法,在非线性条件下可以根据少量的训练数据学习接收信号星座点的分布特性,并相应调整分类判决边界,从而降低误判率. 文献[7]将SVM 用于毫米波无线传输中信号的分类判决,文献[8]将SVM 用于多带无载波幅度相位调制的VLC 系统,解决了采用恒模均衡算法后信号的星座点相偏仍然存在的残留问题.
本文提出使用SVM 对星座点进行分类,以对抗几何整形可见光通信中的非线性效应. 首先介绍几何整形技术和抗非线性SVM 算法的基本原理;然后仿真SVM 在GS-16QAM 系统中的性能,并搭建实验平台进行1.2 Gbit/s 可见光通信高速传输实验. 实验结果验证了SVM在几何整形可见光通信系统中的抗非线性效果——系统误码性能得到了显著提升. 在非线性条件下,圆-169 的GS 星座设计具有最优的符号误码性能;在3.8×10−3的7%FEC 门限条件下,采用SVM 能使系统正常工作的幅度范围提升0.1 V.
1 几何整形技术
在可见光通信系统中,高阶QAM 调制可以带来更高的频谱效率,同时符号间的干扰也随之增加. 因此,为了保证系统的可靠传输就需要更高的信噪比. 然而,由于路径损耗和发散角的影响,接收端信号的信噪比是受限的. 为了降低符号间干扰,提升系统对噪声的容忍度,几何整形技术应运而生. 这项技术可以通过重新设计发射信号星座点分布来提升星座点间的最小欧氏距离,从而降低噪声的影响.
以16QAM 为例,文献[10-11] 从最常用的格型星座设计出发,分别研究了以圆形向外扩展的圆-169 和圆-1555 星座点设计的性能;文献[4]在此基础上提出了具有更大的最小欧氏距离的六角型等设计方案,如图1 所示. 选取了4 种GS-16QAM 星座点:格型、六角型、圆-169 以及圆-1555,其基本参数如表1 所示. 若以最小欧氏距离来衡量,则六角型、圆-169 和圆-1555 相对于格型具有明显的优势,其中六角型具有最大的最小欧氏距离,因此可以预计六角型的抗噪声性能更优.
值得注意的是:根据几何整形星座点排布得到的欧氏距离增益从理论上来说可以降低符号间干扰,进而降低加性高斯白噪声(additive white Gaussian noise, AWGN)信道下的误符号率,但是由于编码映射不同,系统比特误码率也不一定随之降低. 因为格型16QAM 采用了相同错误符号下误码率最小的格雷编码[12],即使错误符号数目一样,格雷编码的错误比特数也是最少的. 这一点不仅在之后的仿真和实验结果中都有所体现,而且圆-169 和圆-1555 在峰均功率比(peak to average power ratio, PAPR)和功率归一化下信号的电压峰峰值Vpp方面明显低于另外两种设计方案. 可见光通信系统通常是功率限制的,这意味着在相同的平均功率条件下,圆-169 和圆-1555 出现高电平的概率低,受到非线性效应的影响小. 此外,信号的同向分量I和正交分量Q的峰值功率和平均功率也已在表1 中给出.

图1 GS-16QAM 星座图设计Figure 1 Constellation designs of GS-16QAM

表1 GS-16QAM 星座图设计的基本参数Table 1 Essential parameters of GS-16QAM constellation designs
图2 展示了4 种GS-16QAM 的互补累积分布函数(complementary cumulative distribution function, CCDF)曲线,CCDF 表示峰均值超过某一门限值PAPR0的概率. 可以看出,格型的CCDF 处于最上面,意味着其高电平出现概率大于其余几种GS星座设计的高电平出现概率,也就是更容易受到非线性效应的影响.
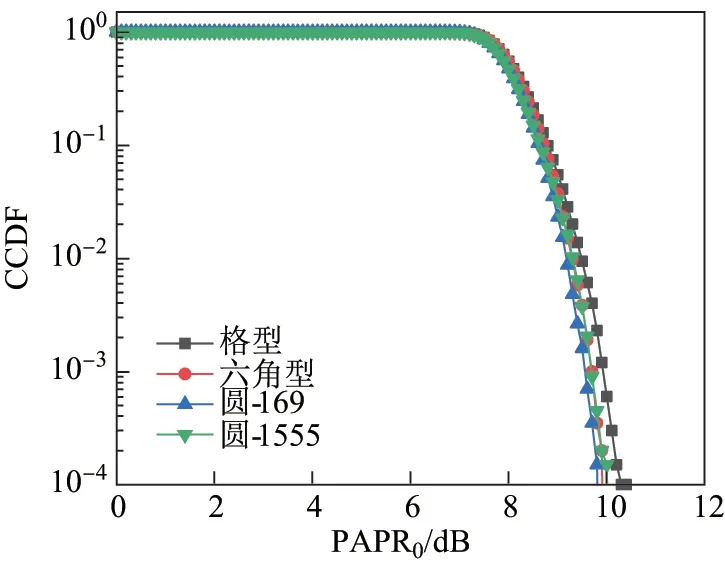
图2 GS-16QAM 星座图设计的CCDF 曲线Figure 2 CCDF curves of GS-16QAM constellation designs
2 抗非线性SVM算法
在可见光通信系统中,由于可见光信道的特殊性以及发射器件LED、接收器件、电路放大器等本身的特性[13-15],信号在传输过程中会受到严重的非线性效应影响,这将使得系统有效工作的电压范围受到极大的限制. 以格型16QAM 信号为例,经过传输后的星座图因噪声的影响而使星座点分布变得分散. 由于非线性的影响,星座点出现移位、变形等失真现象,这对于高电平星座点的影响尤其明显.
传统基于欧氏距离的星座点分类判决方法根据最小欧氏距离,将目标星座点划分到距离最近的标准星座点所属的类别. 这种方法并未考虑信号传输特性,得到的分界平面只与标准星座点分布有关,因此在非线性条件下会造成大量的星座点误判,使误码率大幅度升高,如图3所示. 于是,本文提出使用一种经典的有监督的机器学习算法——SVM,用以找到最优的分类界面. 如图3 右侧所示,SVM 根据少量的训练数据学习接收星座点的分布情况,调整分类判决界面,从而降低误判以提升误码性能. SVM 最初提出时用于二分类,其基本原理如图4所示. 给定一个包含n点的训练数据集(xi,yi),i=1,··· ,n,其中xi为p维的特征向量,yi为标签. SVM 的主要任务是找到能够将两组数据分开的p −1 维的最优超平面,图4中显示了p=2 的情况. 在特征空间中,任意一个超平面可以表示为
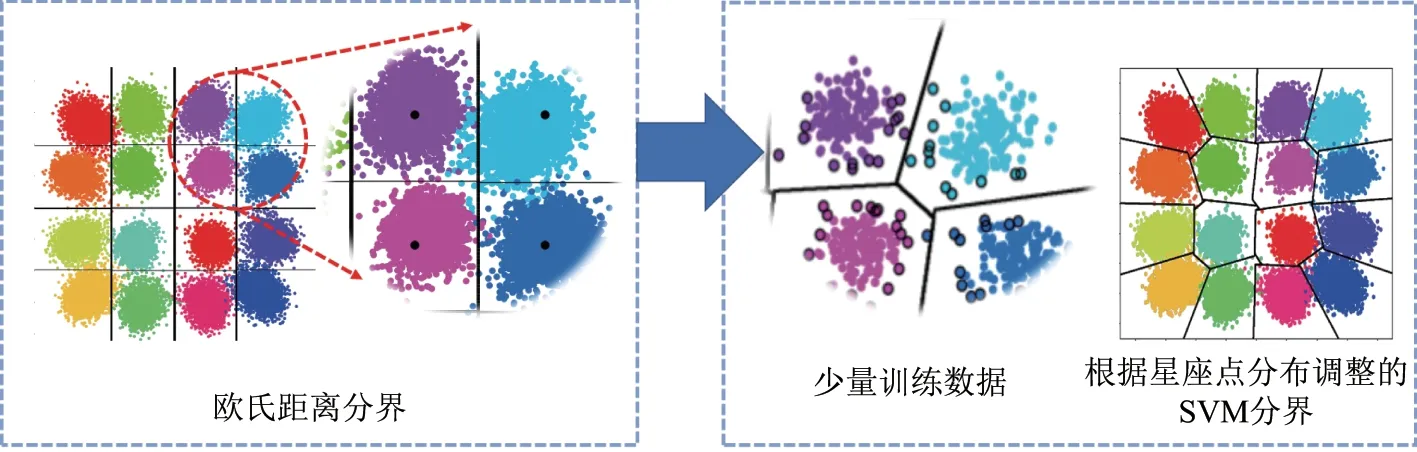
图3 非线性情况下的欧氏距离分界与SVM 分界Figure 3 Classification boundary based on Euclidean-distance and SVM under nonlinearity

式中,ω为平面的法向向量,b为常数项. 如图4 所示,如果给定的训练集是线性可分的,就能找到两组数据的平行边界,可以表示为
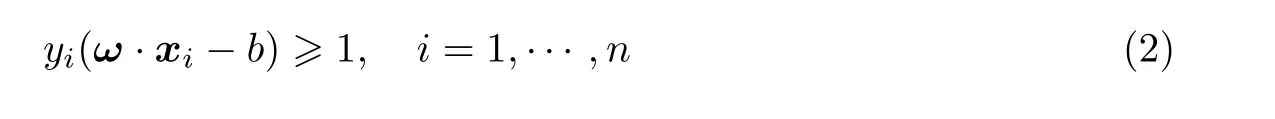
在这两个平行边界之间的超平面则为分类界面,而最优的分类界面应该满足到每个边界的最小距离最大的条件. 两个平行边界之间的距离被称为间隔(margin),其值为2/ ω.为了使间隔最大化,就需要最小化ω. 两组数据中距最优分界面最近的点被称为支持向量(support vectors),可见SVM 得到的分界面只与支持向量有关.
对于无法完全线性可分的情况,为了在错误最少的情况下进行分类,可以设定一些非负的松弛变量ξi,则引入软间隔(soft-margin)的超平面可以表示为
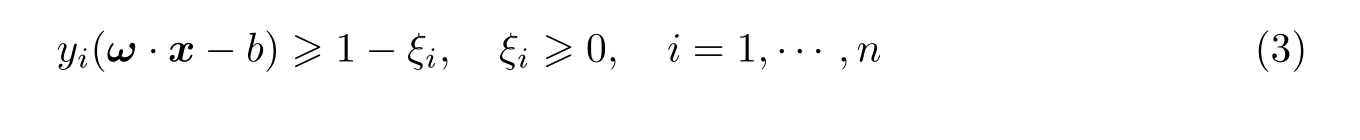
为了得到最优分界超平面的ω和b,需要求解下面的问题[16]:
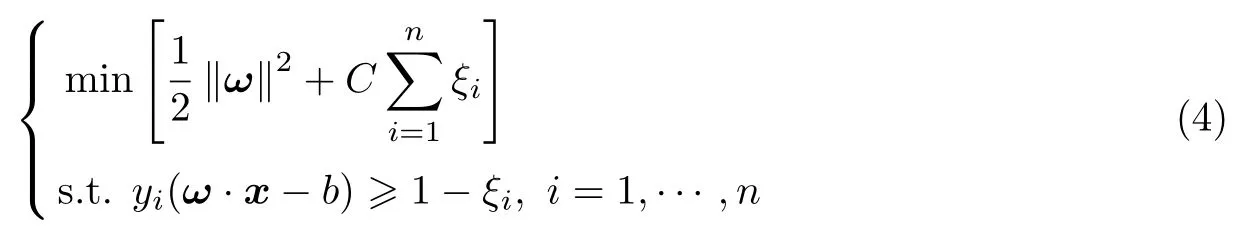
式中,C为惩罚因子. 值得一提的是:软间隔SVM 中松弛变量和惩罚因子的引入起初是为了适应训练集非完全线性可分情况,但是在之后的应用中,人们常通过调整C来去除一些异常的数据点,从而提高训练模型的泛化能力. SVM 的数值求解使用对偶二次凸优化问题的方法.假设最终想要得到的分界超平面形成的分类器以判决函数D(x)表示为

式中,ω0为p维向量,b为常数项,共同决定这个超平面. 因为SVM 得到的最优分界是由l个支持向量决定的,所以ω0可以写成支持向量的线性组合

D(x)化为如下的形式:

根据文献[16]可知:训练集中任意一个(xi,yi)都应满足αi=0或yi(ω·x)−b=1−ξi. 对于前者,此点不会影响SVM 分类器的结果;而对于后者,此点是支持向量. 这就是SVM 的训练步骤.
测试步骤时需要对新输入的数据用上面得到的SVM 分类器进行分类. 首先提取输入数据的特征向量,然后根据式(8)

得到新输入样本的类别预测. 其中sign(·) 被称为符号函数,输入大于0 时取1,小于0 时取–1.从本小节上述的介绍中可以看出,SVM 的一大特点是最终的判决分界只与少数的支持向量有关,这一点在样本预测阶段的高维空间非常有效. 对于线性不可分问题,可以通过核函数将数据映射到高维空间,并在高维空间实现线性可分SVM[17].
将SVM 应用于多分类问题时,首先要建立合适的多分类器,从而将多分类问题转化为二分类问题. 本文根据一对多(one-versus-all, OVA)策略SVM 对GS-16QAM 的星座点进行分类判决. 在训练阶段,在每1 类和其他15 类之间建立SVM 二分类器,最终得到含有16 个二分类器的SVM 多分类模型.
根据文献[19]可知:在训练阶段,SVM 的核心是通过求解二次规划问题从训练数据中分离得到支持向量,这一步骤的复杂度介于O(dN2t)到O(dN3t)之间,其中d为特征向量的维度,Nt为训练集样本数目. 可以看出,随着训练样本的增加,计算复杂度也会快速增加. 因此,为了高效地建立SVM 模型,选择合适的训练数据数目是非常必要的. 在测试阶段,复杂度为O(MNs),其中M为计算核函数的操作数,Ns为支持向量的数目[19]. 因为各星座点之间是线性可分的,所以为了降低模型的复杂度,本文在下面的仿真和实验中都选取了线性核,也就是基础的SVM 形式.

图4 SVM 原理图Figure 4 Schematic diagram of SVM
文献[20] 提出使用另一种经典的机器学习算法K-means 对GS-8QAM 信号进行分类.K-means 是一种不必训练数据的无监督学习的聚类算法,复杂度为O(N),其中N为总数据的数目[21]. 比较而言,SVM 训练步骤的复杂度较高,但SVM 需要的训练数据比例通常很小,而测试阶段的复杂度仅与少数的支持向量和计算核函数操作数有关,因为采用线性核只与支持向量数目有关. 因此,当测试数据很多时,SVM 的复杂度有望低于K-means的复杂度.
3 仿真分析
SVM 应用于GS-16QAM 可见光通信系统的仿真流程如图5 所示. 原始数据首先经过GS-16QAM 映射后得到复数信号;由于LED 低频噪声很大,本文对GS-16QAM 进行4倍上采样和成型滤波后将信号进行频谱搬移而空出低频部分,同时将QAM 信号实数化;然后将产生的实数信号送入可见光仿真信道.

图5 GS-16QAM VLC 系统仿真装置图Figure 5 Simulation setup of GS-16QAM VLC system
对于可见光仿真信道,本文将考虑AWGN和非线性效应的影响,其中非线性效应可以根据振幅比曲线拟合得出[22].
在接收端,信号经过下变换和下采样由实数信号变为I/Q信号;然后采用最小均方(least mean square, LMS)自适应滤波器对信号进行均衡;接着选取一段数据作为训练集,将信号的I路和Q路作为特征进行训练以建立SVM 分类器,进而对接收信号进行分类判决;最后根据SVM 分类判决结果进行解映射以恢复原始数据.
使用SVM 对接收星座点进行分类时,需要考虑训练集比例和惩罚因子C等参数对结果的影响. 若训练集比例过小,则不能代表数据整体的分布情况;若训练集比例过大,则会造成带宽资源的浪费. 根据图6(a)得到的曲线可以看出:随着训练集比例的增加,比特误码率(bit error rate, BER)很快收敛,这正体现了SVM 能够根据少量的训练数据学习总体特征的优点.在后续的仿真和实验中,将选取5%的数据点作为训练集. 惩罚因子C主要反映软间隔SVM 训练模型对差错敏感程度的泛化能力.

图6 比特误码率与SVM 训练集大小及C 的关系曲线Figure 6 Curves of BER versus size of training set and C
随着C以2 的指数倍增加,比特误码率经历了由降低到保持平稳的过程,如图6(b)所示.为了保证模型的准确性,C不可取得太小,于是本文最终选取C=1.
在AWGN 信道下,符号误码率和比特误码率与信噪比(signal to noise ratio, SNR)的关系仿真曲线如图7 所示. 图7(a)给出了符号误码率(symbol error rate, SER)与SNR 的关系曲线,图7(b)给出了BER与SNR 的关系曲线.实线表示未使用SVM,虚线表示使用了SVM.可以看出:随着SNR 的提升,接收星座点分布更加聚拢,因此几种16QAM 的SER 和BER 均随之下降. 在SER 方面,由于六角型、圆-169 和圆-1555 星座点设计的最小欧氏距离大于格型16QAM 的最小欧氏距离,这三者的符号误判概率小于格型的符号误判概率,因此在符号误码性能方面均优于格型,且六角型有着最大的最小欧氏距离,其符号误码率最低,其次是圆-1555. 然而,格型星座点编码采用的格雷映射是最优的. 如图7(b)右所示,在低信噪比的情况下,格型16QAM 的编码增益弥补了最小欧氏距离的不足,因此其BER 低于其余3 种GS-16QAM 星座点的BER. 在没有非线性效应影响的AWGN信道中,使用SVM 的误码性能与未使用时基本相当,甚至由于噪声随机性的影响,使用SVM 后的误码性能可能会不如未使用的情况.

图7 符号误码率和比特误码率与信噪比关系曲线Figure 7 Curves of SER and BER versus SNR
当SNR 为18 且引入了非线性效应时,误码性能与归一化幅度关系的仿真曲线如图8 所示. 需要注意的是:根据表1 可知4 种GS-16QAM 星座点设计产生的信号PAPR 有所不同,且实际VLC系统通常是平均功率受限的. 为了保证4 种GS-16QAM 的平均功率在同一水平,本文以格型16QAM 的归一化Vpp为基准对Vpp进行了换算. 图7(a)给出了SER 与归一化幅度的关系曲线,图7(b)给出了BER 与归一化幅度的关系曲线. 实线表示未使用SVM,虚线表示使用了SVM.
从实线部分可以看到:随着Vpp的增加,信号的星座点开始出现失真和变形现象,尤其是星座图外侧的点——功率较高的点,受到非线性影响更为明显,误码率也随之增加. 在SER方面,由于圆-169 和圆-1555 的PAPR 较小,CCDF 曲线也处于下方,这两种GS 星座点设计的抗非线性性能较好. 从图2 的CCDF 曲线来看,六角型出现高电平的概率低于格型,且在最小欧氏距离方面六角型有着较高的整形增益,因此六角型的SER 总体上低于格型的SER,如图8(a)所示. 然而,格型星座点编码采用格雷映射,如图8(b)所示,当Vpp增加到一定程度时,随着符号误码率的增加,编码增益的优势逐步显现,格型在BER 性能方面优于六角型和圆-1555.

图8 符号误码率和比特误码率与归一化幅度Vpp 关系的仿真曲线Figure 8 Simulation curves of SER and BER versus normalized amplitude Vpp
对比图8 中实线和虚线部分可以看出,4 种星座设计使用SVM 后在误码性能方面都得到了提升,其中格型星座设计使用SVM 后提升最明显. 总体来看,使用SVM 后圆-169 的SER最小,在一定的Vpp范围内BER 性能也是最优的. 当Vpp增加到一定程度时,在使用SVM 的情况下,格型星座点凭借编码增益的优势在BER 性能方面与圆-169 相当,甚至优于圆-169.
当Vpp为1.4 时,GS-16QAM 星座点分别基于欧氏距离分界和基于SVM 分类判决的仿真结果如图9 所示,其中黑色的点代表误判. 可以看到:在非线性条件下,基于SVM 的分界线可以根据星座点的分布特征进行调整,从而降低了误判概率. 非线性效应对星座点造成的影响表现为向高功率方向聚集,同时沿着以原点为圆心的圆的径向扩散拉长. 六角型和圆-1555的设计存在内外圈的星座点径向角度重合的情况,在非线性效应的影响下符号之间干扰十分严重,即使使用SVM,对于误码性能提升也比较有限. 对于格型和圆-169 星座设计,内外圈星座点有一定的交错角度,虽然因非线性效应而产生位移和形变,但是仍存在较为明显的分界,只要通过SVM 就可以找出目标的最优分界. 因此,格型和圆-169 使用SVM 后在误码性能方面有较明显的提升.

图9 GS-16QAM 星座点的基于欧氏距离分界和基于SVM 分类判决的仿真结果(Vpp=1.4)Figure 9 Simulation results of GS-16QAM constellation based on Euclidean distance boundary and SVM classification (Vpp =1.4)
4 实验验证
为了验证SVM 在几何整形可见光通信系统中的抗非线性效果,本文搭建了高速可见光通信实验平台进行验证. 图10 为可见光通信系统实验装置示意图. 根据图5 所示的系统仿真装置图,首先通过MATLAB 离线生成GS-16QAM 数据,然后通过任意波形发生器生成电信号. 本实验控制AWG发射速率为每秒1.2G 符号,考虑到可见光通信系统在高频部分存在严重的衰减现象,在发射端使用均衡器对信号进行预均衡;然后经放大器放大后通过偏置器和直流信号耦合驱动LED发光. 本实验选用的发射光源峰值波长为457 nm 的蓝光LED[24],传输信道为2.5 m 水下可见光信道. 接收端使用透镜和光阑调节接收功率,使用PIN 光电二极管将光信号转化为电信号,其中PIN 型号为Hamamatsu S10784,波长响应范围为340~1 040 nm,峰值灵敏度波长为760 nm,灵敏度典型值为0.52 A/W,并以差分输出减小共模噪声. 经示波器采样后,对信号进行离线数字信号处理,其具体流程已在图5 中介绍.

图10 可见光通信系统实验装置图Figure 10 Experimental setup of VLC system
误码性能与信号幅度关系的实验结果如图11 所示. 与图8 相似,横坐标Vpp以格型16QAM 的归一化Vpp为基准,并根据PAPR 进行换算. 图11(a)给出了SER 与信号幅度的关系曲线,图11(b)给出了BER 与信号幅度的关系曲线. 实线表示未使用SVM,虚线表示使用了SVM. 从实线部分可以看出:随着Vpp的增加,信号受到非线性影响的程度加剧,星座点的移位和变形更为严重,误码率随之上升. 在SER 方面,与仿真结果基本相符,六角型、圆-169和圆-1555 在符号误码性能方面均优于格型,其中圆-169 的SER 最低,六角型和圆-1555 性能基本相近. 同样在BER 方面,随着Vpp的增加,错误符号数目也随之增加,格型的编码增益优势逐步体现,其BER 性能逐渐优于六角型和圆-1555.
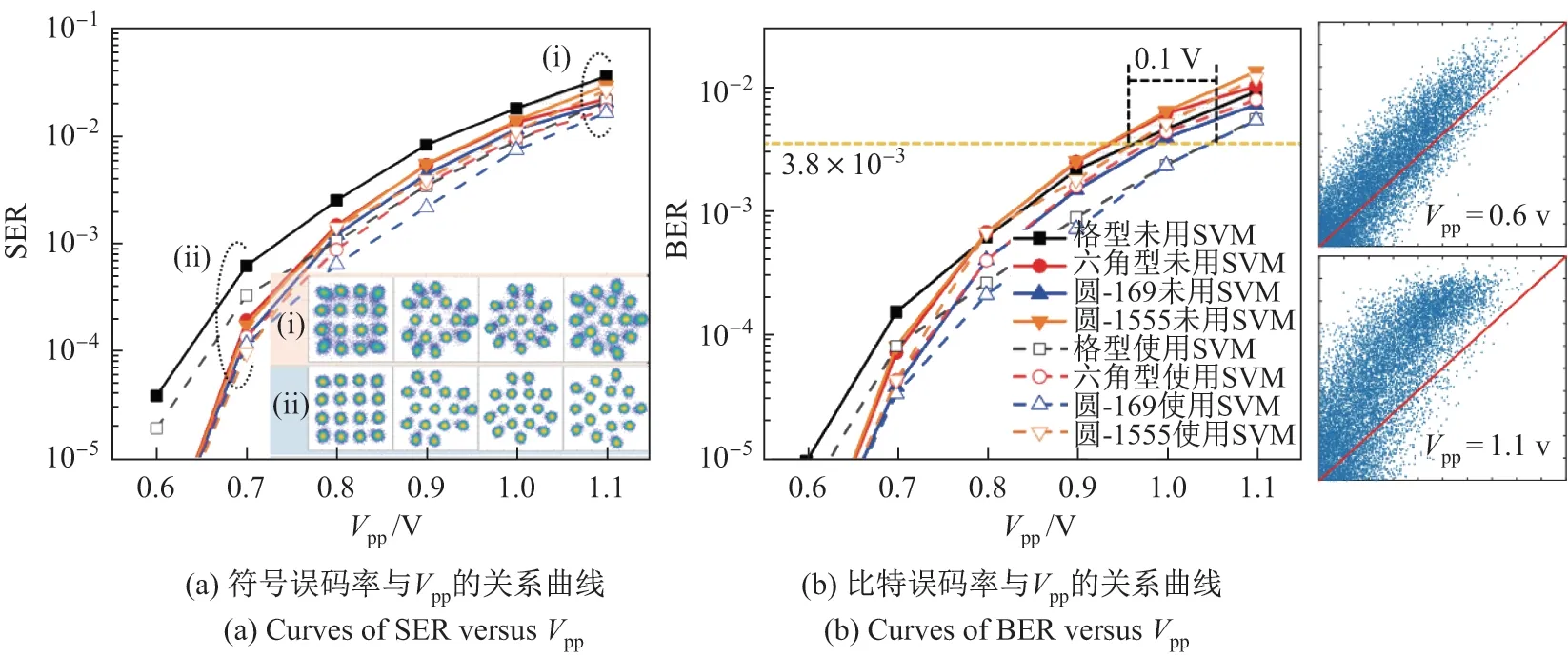
图11 符号误码率和比特误码率与Vpp 的关系曲线Figure 11 Curves of SER and BER versus Vpp
对比图11 中的实线和虚线部分可以看出,4 种16QAM 星座设计使用SVM 后在误码性能方面都得到了提升. 其中,使用SVM 后圆-169 的SER 性能最优. 在Vpp小于1.0 V的情况下,圆-169 使用SVM 的BER 最小;随着Vpp的增加,圆-169 使用SVM 与格型使用SVM 的性能逐渐相近;最终在3.8×10−3的7%FEC 门限且使用SVM 的情况下,系统能够工作的Vpp范围相比于基于欧氏距离判决的格型16QAM 信号,由约0.952 V 提升至约1.052 V,即提高了0.1 V.
当Vpp为1.0 V 时,GS-16QAM 星座点分别基于欧氏距离分界和基于SVM 分类判决的实验结果如图12 所示,黑色的点代表误判. 与仿真结果类似,由于受非线性效应的影响,使用基于欧氏距离的分界会造成大量的误判;而基于SVM 的分类判决考虑了接收信号的星座点分布特征并相应地调整了分界面,因此降低了误符号率. 正如第3 节所分析的,由于提出的这几种GS-16QAM 星座设计不同,受到非线性效应的影响后星座点混叠程度也不同,用SVM对于系统性能的提升程度也有所不同,其中以格型和圆-169 的误码率性能提升最为明显.
5 结语

图12 GS-16QAM 星座点的基于欧氏距离分界和基于SVM 分类判决的实验结果(Vpp =1.0 V)Figure 12 Experimental results of GS-16QAM constellation based on Euclidean distance and SVM classification (Vpp =1.0 V)
为了研究几何整形16QAM 星座点在非线性效应影响下的性能,同时对抗可见光通信系统中非线性效应引起的性能恶化,本文提出将有监督的机器学习算法SVM 应用于几何整形可见光通信系统. 首先介绍了几何整形的基本原理,并给出了所使用的GS-16QAM 星座设计的基本参数;然后说明了在非线性条件下传统星座点判决方法的局限性,并介绍抗非线性SVM 算法的基本原理;接着通过仿真研究了抗非线性SVM 算法,既分析了训练集大小、惩罚因子C对SVM 分类效果的影响,又分析了GS-16QAM 未使用/使用SVM 情况下的误码性能随AWGN 信道的SNR 和非线性条件下归一化幅度的变化关系;最后搭建高速可见光通信实验平台进行实验验证. 仿真和实验结果显示,SVM 具有显著的抗非线性性能,在数据速率为1.2 Gbit/s、传输距离为2.5 m 的水下可见光通信传输中,使用SVM 能使GS-169 的符号误码性能达到最优,并使7%FEC 门限下的系统工作幅度范围比基于欧氏距离判决的格型16QAM提高了0.1 V.
