经典物理层高速密钥分发研究进展

高 华，王安帮，王云才

1. 新型传感器与智能控制教育部重点实验室(太原理工大学)，太原030024

2. 太原理工大学物理与光电工程学院, 太原030024

3. 广东工业大学信息工程学院，广州510006

4. 广东省光子学信息技术重点实验室，广州510006

信息加密传输是网络空间安全的核心技术之一. 目前使用的加密技术主要是算法加密，包括对称算法加密、非对称算法加密两种技术. 对称加密是通信双方采用相同的数学算法和种子产生一致密钥；非对称加密则通过大数因子分解等数学难题产生一对公钥和私钥，然后利用公钥加密、私钥解密. 随着计算能力的飞速提升，算法加密在原理上始终存在着被破解的可能性. 例如，非对称加密RSA-768 和对称加密AES-256 技术先后于2009年和2017年被破解.

根据Shannon“一次一密”理论，安全的保密通信需要通信双方拥有相同的随机数作为密钥，其速率既不能低于数据速率又不能重复使用[1]，因此密钥的高速分发是保密传输最重要的核心技术.

量子密钥分发是基于量子不可克隆和测不准原理的物理层密钥分发方法[2]，受到了广泛的关注和国家持续强有力的支持. 以潘建伟院士为代表的中国学者率先开展了示范工程探索，如2016年“墨子号”量子科学实验卫星成功发射，2017年“京沪干线”量子保密通信示范线路首次调试，实现了大于20 kbit/s 的密钥分发速率. 未来量子密钥分发研究亟需攻克密钥速率瓶颈以及与现有光纤通信系统兼容等关键问题.

在宽带中国战略指引下，宽带通信已经进入千兆接入网、100G 骨干网时代，这对信息加密技术提出了更高的要求. 因此，研究者们不断探索基于经典物理原理的高速安全密钥分发技术，以期实现密钥分发速率的突破. 迄今为止，已报道的经典密钥分发方案主要基于光纤激光器参数随机选择、物理不可克隆函数、光纤信道噪声以及混沌激光同步等技术. 本文将简述上述4 种方案的基本原理及主要研究进展.

1 基于光纤激光器参数选择的密钥分发

2006年，Scheue 和Yariv 提出基于光纤激光器波长随机选择的密钥分发方案[3]，其原理如图1(a)所示. 通信双方Alice 和Bob 分别控制光纤激光器两端腔镜的反射中心波长并对其进行编码（λ0和λ1分别为0 和1），独立地随机选择中心波长进行密钥分发. 当双方选择相同波长时，激光器输出相应波长的激光；当双方选择不同波长时，激光器均输出波长为λT=(λ0+λ1)/2的激光. 对于后者，窃听者Eve 无法确定通信双方的选择，因而可用于密钥分发. 双方根据探测激光器中心波长和己方的波长选择确定对方的波长选择情况后进行密钥分发. 2008年，Scheue 等对此方案进行了实验验证，实现了距离为25 km、速率为167 kbit/s的密钥分发[4]，实验结果如图1(b)中的蓝色和红色曲线所示. 当Alice 和Bob 处于01 和10 两种波长选择状态时，激光器的光谱重叠，难以区分.

增加λ0与λ1波长间隔使相应反射谱无交叠，则当双方选择不同波长时，激光器从λT状态变为无激光振荡的暗态，如图2(a)中0 1 和1 0 两个状态. 利用光纤激光器暗态进行密钥分发可以提高安全强度，如图2(b)所示，由此可见从激光器输出强度的时间序列上无法区分两个暗态.

图1 基于光纤激光器波长选择的密钥分发Figure 1 Key distribution using wavlength selection of fiber laser

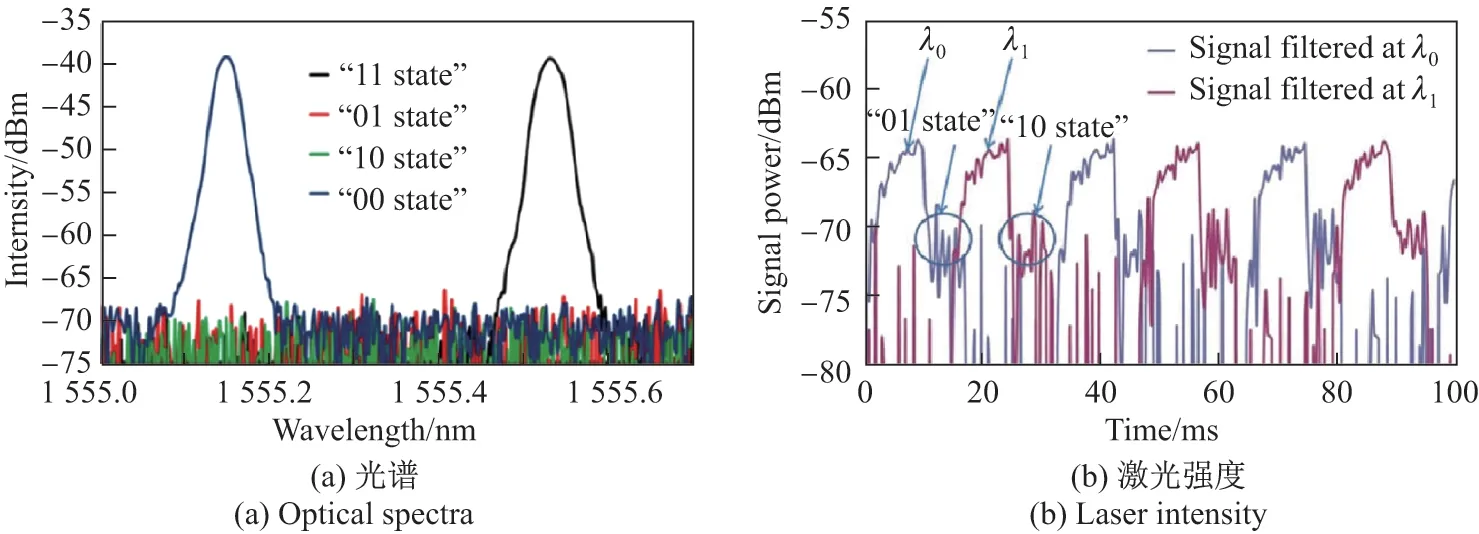
图2 利用光纤激光器暗态的波长选择密钥分发[6]Figure 2 Key distribution based on dark state of fiber laser with wavelength selection[6]

2015年，Tonello 等提出腔长随机选择的密钥分发方案[5]. 相似地，通信双方各自利用一段光纤独立随机地改变光纤激光器的腔长，从而控制激光器纵模间隔：当两者跳线长度的选择不同却能保证腔长不变时，激光器纵模间隔保持不变，窃听者无法得知通信双方的具体选择，显然可以进行密钥分发.

对于此类光纤激光器参数选择密钥分发方案，可以利用拉曼增益增加分发距离[6]，如El-Taher 等实现了距离为500 km、速率为100 bit/s 的密钥分发；也可以通过波分复用提高密钥分发速率[7]. 这类方案中使用连续光纤激光器，其增益由掺铒光纤放大器[3-5,7]或拉曼放大器[6]提供. 然而，通信双方每传输1 bit 密钥，腔内光场须至少往返一周，故在原理上光纤激光器密钥分发速率与腔长即传输距离成反比. 实现长距离、Gbit/s 量级的高速密钥分发需要原理性突破.

2 物理不可克隆函数

物理不可克隆函数（physical unclonable function, PUF）是内在构造具有唯一性和复杂性的物理实体内，对任一激励信号可产生唯一且不可预测的响应信号. 光学散射体是一种典型的PUF.

2013年，Horstmeyer 等提出基于光学散射体PUF 的密钥分发方案并进行了实验验证[8]，其原理如图3所示. Alice 和Bob 利用各自散射体作为PUF，将预设空间分布p1,···,n的入射光映射成一系列散斑图样，然后转换为随机数密钥k1,···,n(A)、k1,···,n(B). 双方将异或k1,···,n(A)⊕k1,···,n(B)作为公钥与激励p1,···,n一同保存在公共数字电子词典中. 通信时，Alice 通过激励与PUF A 重新生成私钥用于加密；Bob 使用相同激励及PUF B 生成其私钥，再与词典中的公钥进行异或计算即可获得Alice 私钥，从而进行解密.

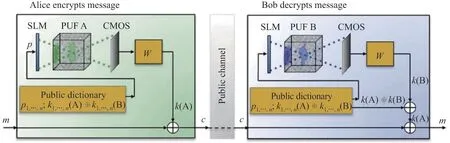
图3 基于物理不可克隆函数的密钥分发原理图[8]Figure 3 Schematic diagram of key distribution based on physical unclonable function[8]

根据原理可知，利用物理不可克隆函数产生随机密钥的长度有限，因此密钥必定会被重复使用，但这不满足Shannon“一次一密”的要求，难以承受已知明文的攻击. 此外，物理散射体结构特性的长期不稳定性会导致公钥失效，因此双方需要定期“会晤”以更新数字电子词典，不过这个过程可能会带来不安全因素.

3 光纤信道噪声

1993年，Maurer 等从理论上证明：在一定条件下，通信双方可以采样量化具有相关性的噪声熵源，并在异地同时产生一致随机数作为密钥，从而实现信息论安全的密钥分发[9]. 这个理论最早用于无线通信，利用无线信道的短时互易性使双方获得相同的信道噪声，进而产生一致密钥；信道的路径相关性可防止窃听[10]. 然而，受限于环境噪声带宽、大气传输损耗等因素，无线通信密钥分发速率低且距离短.

2013年，Prucnal 等提出利用光纤信道噪声互易性进行密钥分发[11]，通过实验实现了传输距离为26 km、速率为160 bit/s、误码率小于0.04 的密钥分发，其原理如图4(a)所示. 通信双方Alice 和Bob 之间构建光纤马赫-曾德尔干涉仪，利用双臂干涉测量光纤信道中的相位噪声. 根据干涉原理，干涉仪输出功率正比于x=(1+cos∆φ)/2，其中∆φ为双臂之间的相位差；根据路径互易性，双方观测到的功率波形具有高度相关性. 因此，对x(t)采样量化可异地同时产生共享随机密钥. 需要指出的是，双方需要采用宽带光源注入干涉仪以防止窃听者直接测量相位变化，有利于提高安全性. 此方法的安全性也来自于信道噪声的路径相关性，即因位置不同窃听者无法获得与通信双方相关的信号.

2018年，胡卫生教授等提出基于正交偏振模延迟干涉的密钥分发方法[12]，其原理如图4(b)所示. Alice 和Bob 利用一根保偏光纤构建偏振模延迟干涉仪，从干涉仪一端注入线偏振光，经过偏振器后激发得到两个正交偏振模式. 由于偏振模色散的存在，两者经过保偏光纤传输后的相位差为∆φ=2π∆nL/λ，其中λ为波长，∆n为两个偏振模式的折射率之差，L为保偏光纤长度. 此相位差对外界环境变化（如温度、压力和机械变化）高度敏感而随时间随机变化. 根据路径互易性理论，双方注入线偏光之后所测量到的偏振模干涉光强度I相同并且仅与偏振模式相位差有关，可以用作熵源产生共享随机密钥. 此方案通过实验实现了传输距离为25 km、速率为220 bit/s、误码率为0.05 的密钥分发. 同年，该课题组基于类似原理利用偏振态的斯托克斯参量实现了传输距离为25 km、速率为213 bit/s 的密钥分发[13].

2019年，Bromberg 等提出利用多模光纤中的模式随机混合进行密钥分发[14]，其原理如图4(c)所示. 通信双方根据单模光纤与多模光纤耦合位置选定光在多模光纤中的传播路径，并借助该路径的互易性和唯一性实现密钥安全分发. 实验利用波段为1 550 nm、纤芯直径为62.5 µm 的多模光纤实现距离为1 km、速率为20 Hz 的密钥分发. 由于多模光纤损耗大，该方案无法实现长距离密钥分发.

图4 基于光纤信道噪声的密钥分发Figure 4 Key distribution based on fiber channel noise

在上述基于光纤信道噪声的密钥分发方案中，密钥速率受噪声信号带宽限制. 以如图5 所示的马赫-曾德尔干涉仪方法为例，相位噪声带宽随着干涉仪臂长的增加而增加，表明干涉仪越长对外界噪声越敏感，但即使在臂长为26 km 的情况下，信号频宽也只有1 kHz[11]. 若增加光纤距离，将难以保持信道传输互易性——信道两端噪声特征的一致性. 2019年，胡卫生教授课题组引入有源偏振扰动器来加速偏振态的随机波动，实现了速率为200 kbit/s 的密钥分发[15].

2019年，张杰教授等提出利用信道误码率测试进行密钥分发[16]，其基本原理是数字信号在链路传输中的误码率互易性，如图6 所示. Alice 发送的信息传送给Bob，后者解调后再回传，这样Alice 就可以测量链路噪声引入的误码率——通过短时、连续测量可得到误码率随时间的随机波动；根据信道互易性，Bob 也可以得到高度相似的误码率波动序列. 双方对同步的误码率波动信号进行采样量化后产生一致随机数以实现密钥分发，并通过实验实现了传输距离为200 km、速率为2 Mbit/s、误码率为0.02 的密钥分发. 该方法避免了光纤信道噪声带宽的限制，但其密钥速率受限于误码率测量时间.

图5 马赫-曾德尔干涉仪中相位波动的频谱Figure 5 Spectra of phase fluctuation in Mach-Zehnder interferometer

4 基于混沌激光同步的密钥分发

混沌激光因其宽频谱、大振幅的随机起伏特性而用作物理熵源产生高速随机数[17]. 此外，两个混沌激光器在结构、参数匹配条件下可以实现混沌同步[18]，产生高度相关的混沌波形，因此可以根据Maurer 理论利用混沌激光同步进行密钥分发. 目前，基于混沌激光同步的密钥分发可以分为混沌掩藏私钥交换、键控混沌同步密钥分发两类方法.

混沌激光的频谱带宽可达数十GHz，作为物理熵源实时产生随机密钥的速率可达20 Gbit/s[19]；且混沌激光带宽不会受长距离传输影响，可见基于混沌激光同步的密钥分发速率与传输距离不相关，因此这类方案有望实现Gbit/s 量级的长距离密钥分发.

4.1 混沌掩藏私钥交换

2010年，Kanter 等首次提出混沌掩藏私钥交换方案[20]. 2016年，Porte 等通过实验实现了速率为11 Mbit/s 的背靠背密钥分发[21]，其实验装置如图7(a)所示. 通信双方利用参数匹配的半导体激光器互耦合实现混沌同步，注意图中由环形器构成的光纤环同时起到光反馈和光注入的作用. 双方将各自私钥信号m1(t)和m2(t)经激光器电流调制后掩藏于混沌载波之中并传输给对方，然后利用混沌同步的激光器分离出混沌载波和私钥信息以实现私钥交换，再对比私钥挑选出一致的部分作为共享密钥，实验结果如图7(b)所示. 然而，该方法将混沌载波暴露于公共信道，易被窃听者获取并通过强注入锁定同步[20]，因此需要研究大参数空间的混沌激光收发机，以提升安全强度.

图7 混沌掩藏私钥交换[21]Figure 7 Private key exchange by chaos masking[21]

4.2 键控混沌同步密钥分发方法

4.2.1 原理

为了避免混沌信号在公共信道中传输，2012年日本NTT 通信实验室Yoshimura 等提出混沌同步密钥生成方法[22]，基本思路是利用随机光源驱动通信双方的光反馈半导体激光器以实现混沌同步，再对同步混沌波形进行采样量化产生一致的随机数，其原理如图8 所示. 通信双方利用参数匹配的光反馈激光器在同源宽带随机光驱动下实现混沌同步，同时独立且随机地键控反馈光相位（0 或π）以实现键控混沌同步，即当键控相位同相时双方激光器输出CA、CB混沌同步，否则无相关性. 通信双方对混沌信号采样后量化产生初始随机码RA和RB，然后根据键控参数筛选出同相键控时对应的随机数作为一致密钥KA和KB，以实现密钥分发.

图9(a)为键控混沌同步密钥分发首次实验报道的装置图[22]. 驱动光信号为相位噪声调制的连续光，通过60 km 色散位移光纤传输后分别驱动两个响应激光器实现混沌同步，并调制对反馈光的相位来键控混沌同步，典型同步键控结果如图9(b)所示. 图中上方两个波形分别为响应激光器1 和2 的相位键控波形，下方波形为两个激光器混沌输出的短时互相关曲线. 可见，当通信双方同相调制时，响应激光器混沌同步，其同步系数约为0.9；当反相调制时，短时互相关值降至0，响应激光器无相关性. 通信双方进一步选择同相调制对应的同步混沌信号进行采样量化产生一致密钥. 为降低噪声干扰，通常采用双阈值量化，其原理如图9(c)所示. 以混沌波形的均值V0和标准差σ来设置高、低两个比较阈值V1,2=V0±k1,2σ. 当某采样时刻的混沌强度大于高阈值V1时量化为“1”码，小于低阈值V2时量化为“0”码；否则，舍弃该采样点. 优化调节两个比较阈值，可以有效降低误码率并产生一致的随机码. 该实验成功实现了传输距离为120 km、速率为182 kbit/s 的密钥分发.

键控混沌同步密钥分发被证明是一种基于有界观测的信息论安全的密钥分发[23]. 首先，驱动信号与产生密钥的混沌熵源不相关，窃听者就无法直接从驱动信号观测到足够的熵源信息；其次，只有结构和参数匹配的混沌激光器才能实现混沌同步，这需要从同一片晶圆上精心挑选激光器芯片才能实现，故可认为窃听者无法获得匹配的窃听激光器，与合法激光器的互信息量很低；最后，混沌状态的随机键控迫使窃听者需要同时仿制更多窃听激光器，增大了破解难度. 基于上述3 点，窃听者所能观测到熵源的信息量远小于合法通信双方，显然可以实现信息论安全的密钥分发. 2013年，Uchida 等利用了键控两级级联的响应激光器混沌同步的方案，提高了密钥分发的安全性[24]. 除了增加响应激光器的级联数目之外，对键控参数进行多态键控也可以增加安全性. 然而，只有当所有键控态相同时才能够同步，因此多级响应激光器级联或者多态键控会导致密钥分发速率降低.

上述方案是从同步状态的混沌序列中抽取一致密钥. 2017年，江宁等提出一种基于混沌同步的键控态密钥分发方案[25]，其原理如图10(a)所示. 混沌同步及键控方式与前述方法相同；不同之处在于双方交换混沌信号，并通过混沌同步与否判断两种的键控状态是否一致，挑选其中状态一致的键控参数作为共享密钥. 该方法无需高速随机数产生部分，简化了系统. 然而，判断键控态是否一致并不需要高质量的混沌同步，因此该方法对激光器参数匹配的要求低于同步随机数生成方法，其安全强度相对较低.

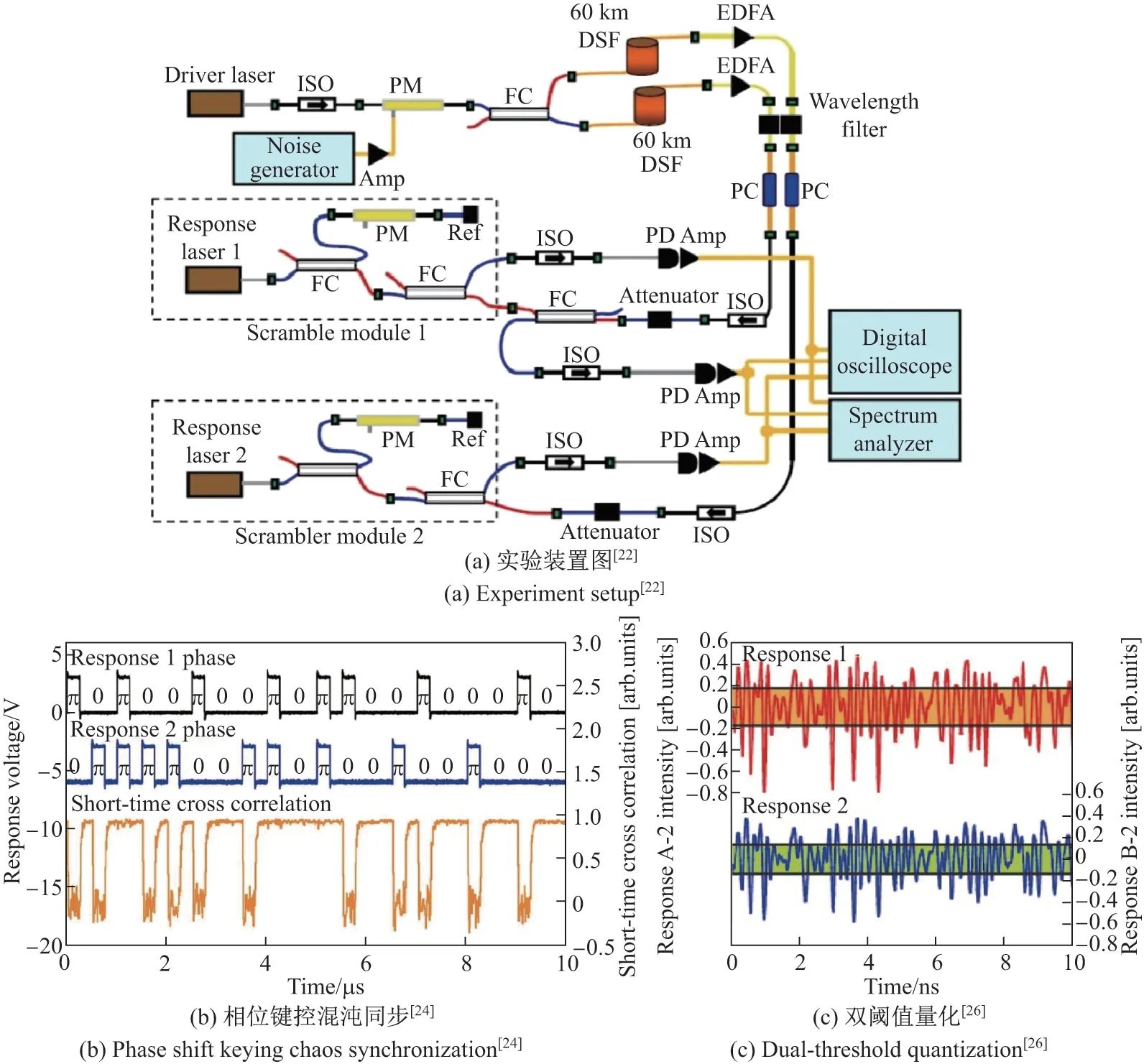
图9 基于键控激光器混沌同步的密钥分发Figure 9 Key distribution using chaos shift keying synchronization

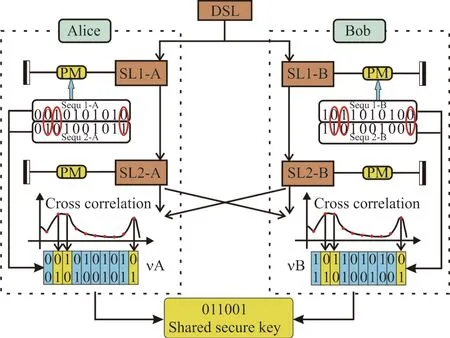
图10 键控态随机选择的密钥分发[25]Figure 10 Key distribution using random selection of keying parameter[25]

4.2.2 密钥分发速率限制及相关研究进展

相比于信道噪声等其他方法，混沌激光同步密钥分发具有以下优点：一是熵源带宽可达数十GHz，二是在分发原理上密钥速率与传输距离不相关. 因此，最有潜力实现Gbit/s 量级的高速长距离密钥分发.

然而，实验报道的键控混沌同步密钥分发速率仅为100 多kbit/s，主要受限于混沌同步恢复时间. 在混沌键控过程中，通信双方的混沌激光器从不同步恢复到同步需要经过一个缓慢过程，如图11 所示. 对于分布反馈式（distributed feedback, DFB）半导体激光器，其同步恢复时间可达68 ns[26]. 键控周期只有大于同步恢复时间才能获得有效的高质量混沌同步序列，从而产生一致密钥. 因此，同步恢复时间成为限制密钥分发速率的主要因素.

为了提高密钥分发速率，研究人员在以下几个方面展开了研究与探索. 2017年，Uchida等尝试以单片集成方法缩短激光器外腔长度来缩短混沌同步恢复时间[26]，然而实验结果表明，缩短响应激光器外腔长度可以提高混沌同步的稳定性，但不能有效缩短同步恢复时间. 同年，江宁等根据理论研究发现，垂直腔面发射激光器（vertical-cavity surface-emitting laser,VCSEL）具有约20 ns 的同步恢复时间[27]. 2019年，刘德明教授课题组从理论上探索在光电振荡器中引入光反馈DFB 激光器[28]，但还是通过键控激光器反馈相位进行密钥分发，其同步恢复时间并未得到明显降低.

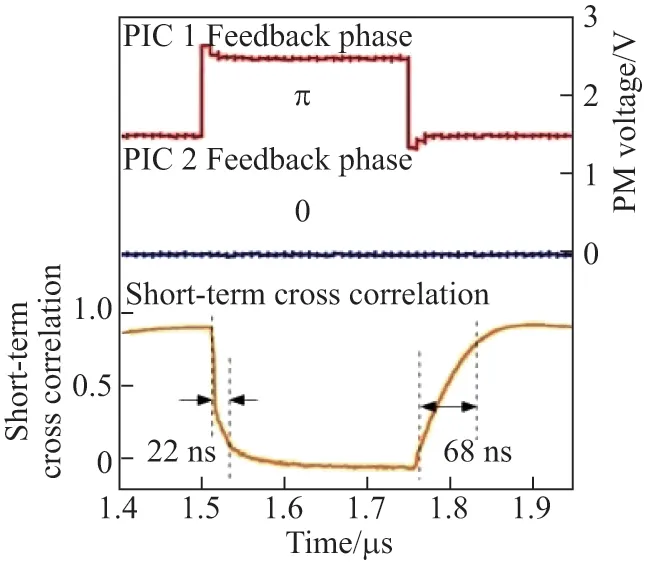
图11 混沌同步恢复时间[26]Figure 11 Chaos resynchronization time[26]

4.2.3 仍需解决的关键问题

经分析可知，目前混沌键控同步密钥分发技术主要面临以下关键问题：

1）关于如何提高密钥分发速率. 目前尚未找到有效缩短混沌同步恢复时间的方法，仍需从混沌同步恢复机理研究出发，探寻如何将同步恢复时间缩短至ns 量级以下，从根本上提升密钥分发速率.

2）关于如何实现高质量混沌同步. 同步误差影响每个采样时刻随机数的一致性，降低一致密钥的生成比率. 因此，混沌同步密钥分发比传统混沌载波通信对同步误差更敏感，无法像后者那样通过优化信息幅度减小同步误差的影响. 此外，密钥分发也不同于单独的随机数产生，若引入延迟差分比较、多位量化等随机数优化技术，反而会引入更多的噪声而不再适用.因此，需要探索高质量混沌同步方式以及抑制长距离光纤传输时放大器自发辐射噪声、光纤色散、非线性等影响的方法，是面向城域网和城际网的实际应用并实现百km 距离密钥分发的关键.

图12 基于模拟数字混合光电混沌源同步的密钥分发[27]Figure 12 Key distribution based on synchronization of analog-digital hybrid electro-optic chaotic sources[27]

3）关于如何提高安全强度. 混沌同步密钥分发安全强度取决于熵源的可观测界限，体现在两方面，即仿制合法熵源的难度以及仿制激光器与熵源之间的互信息量. 这要求混沌激光熵源不仅具有多维度、大空间的硬件参数，同时具有宽带、平坦的频谱特性. 目前报道所用熵源是结构简单的镜面反馈半导体激光器，均无法满足上述要求. 因此，密钥分发的安全强度有待提升.

5 结语

本文综述了基于物理不可克隆函数、超长光纤激光器参数选择、光纤信道噪声、混沌激光同步等几种主要的经典物理层密钥分发技术及研究进展，将能够产生无限长度密钥的后三者技术及已报道的典型实验结果总结在表1 中. 基于光纤激光器的密钥分发实现了500 km 传输距离，但其分发速率与传输距离成反比，仅为100 bit/s. 基于光纤信道噪声的密钥分发速率受到了环境噪声带宽等限制，密钥分发速率低于Mbit/s 量级. 混沌掩藏私钥交换的安全强度低于键控混沌激光同步的密钥分发方法，而后者基于光反馈DFB 激光器（optical feedback DFB, OF-DFB）已经实现百km、百kbit/s 量级的密钥分发，其密钥分发速率受限于同步恢复时间.

鉴于混沌激光熵源带宽可达数十GHz 量级，且基于混沌同步密钥分发的密钥速率在原理上与传输距离不相关. 因此，相较而言，混沌激光同步密钥分发技术最具有实现Gbit/s 量级高速长距离密钥分发的潜力，目前亟需解决快速同步恢复、高质量混沌同步等关键科学问题.

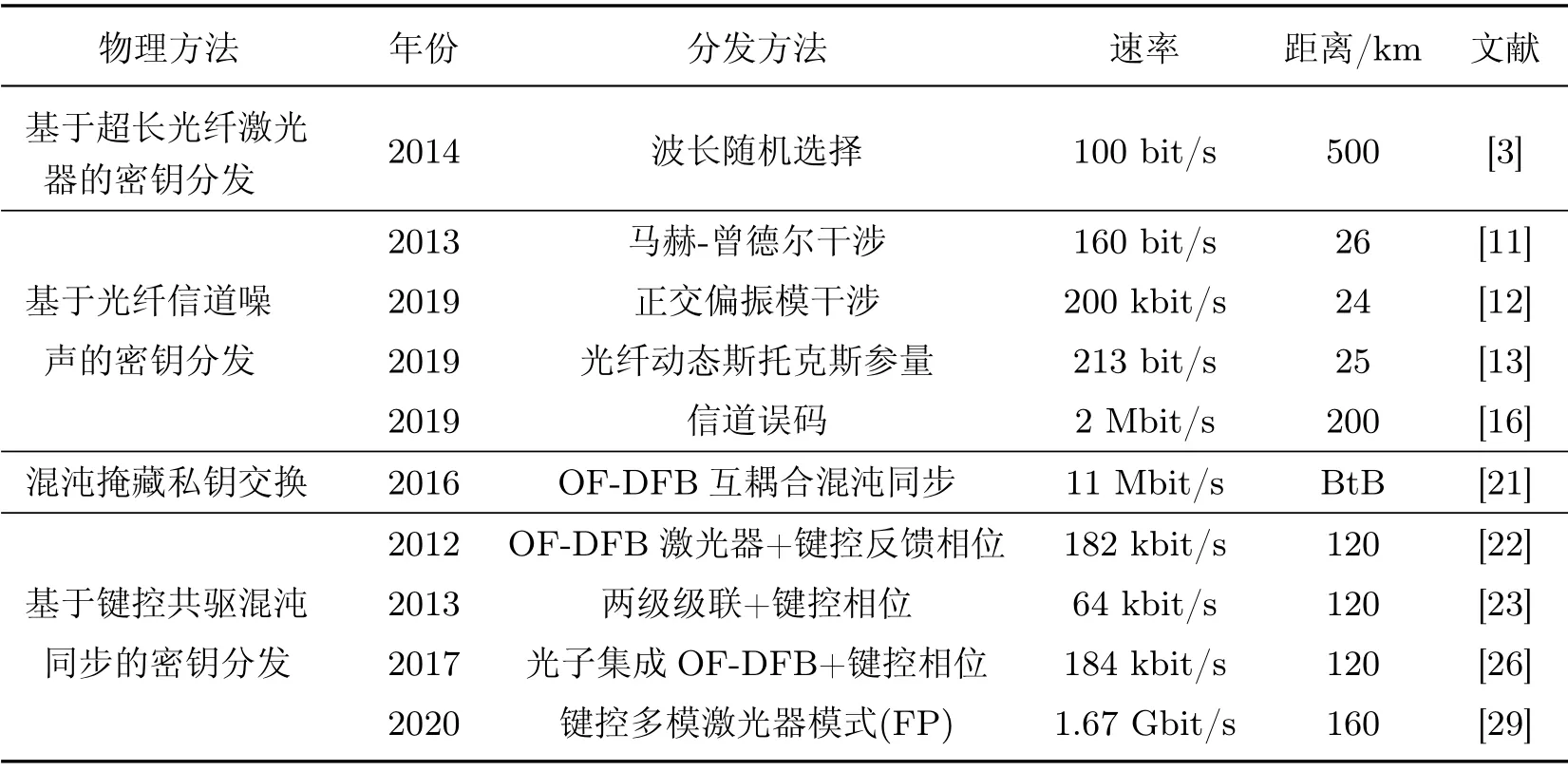
表1 经典物理层密钥分发的主要实验结果Table 1 Main experimental results of key distribution in classical physical layer