大扭矩膜盘联轴器设计及强度分析*

宋 晨，刘 文，马武杰

(重庆大学机械传动国家重点实验室，重庆 400044)

0 引 言

膜盘联轴器如图1所示，是一种通过极薄的变厚度圆盘型面来传递扭矩的挠性联轴器，具有结构简单、无需润滑、运行平稳、振动小、噪声低等优点。其工作原理为转矩从主动端半联轴器输入，经过沿圆周间隔布置的主传扭高强度螺栓将转矩传输至膜盘组，再由膜盘组通过高强度螺栓传至中间轴，并同样由另一端的膜盘组、高强度螺栓及从动端半联轴器输出。

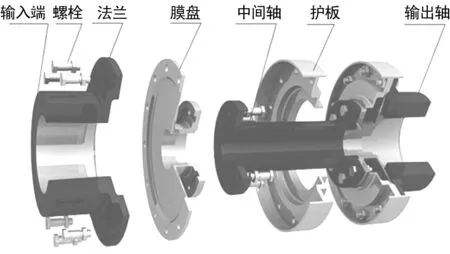
图1 膜盘联轴器的结构

膜盘作为金属膜盘挠性联轴器的关键部件，工作时膜盘联轴器的型面不仅在输入和输出端之间传递转矩，还要通过其弹性变形补偿输入和输出端的位移偏差等[1]。膜盘联轴器运行时，通常受到离心力、扭矩、轴向变形以及角向变形等载荷的作用，其工况参数复杂，这使得膜盘联轴器的关键构件—膜盘成为了膜盘联轴器设计的关键。

膜盘联轴器膜盘的构型存在不同的设计方法，邱兆国等给出在扭矩作用下，盘面断面的近似等强度曲线[2]；李波等根据等强度理论设计了一种以n型结构连接的双膜盘结构膜盘联轴器[3]；李琳等提出了一种基于膜盘联轴器动力学分析和疲劳寿命理论的型面设计方法[4]。针对膜盘联轴器的强度、刚度分析，宣旗等利用理论计算方法对膜盘联轴器膜盘进行了受力分析[5]；艾平贵等基于ANSYS对膜盘联轴器膜盘的应力与模态进行了分析[6]；朱可柯等假设膜盘轮缘与轮毂完全刚性、盘面圆半径不变，基于理论分析，得到了大变形纯扭转下膜盘联轴器的应力应变[7]；岳彭等系统分析膜盘的基本工况和受力模型，基于有限元法计算了膜盘强度[8]；曹安港等对锥形膜盘在各载荷作用下应力分布情况进行仿真分析，并分析了膜盘的扭转刚度、轴向刚度和角向刚度[9]。

可以看出，上述文献中均针对膜盘进行分析研究，而没有考虑膜盘联轴器其他构件对膜盘的影响作用。本文根据膜盘联轴器的传动特点，基于大扭矩这一特点，设计了膜盘等强度型面、内外径比等参数，建立了一种n型型面、高强度螺栓联接的膜盘联轴器整体模型，并基于ANSYS对膜盘联轴器整体模型进行扭矩、角向补偿、轴向补偿以及综合工况的强度分析。

1 膜盘联轴器的设计

1.1 膜盘组件的设计

图2 膜盘型面类型

根据膜盘联轴器设计要求，膜盘联轴器输入功率P=20 000 kW，输入转速n0=7 500 r/min，计算可得其传递扭矩为T=25.46 kN·m，可以看出所设计的联轴器需要传动大扭矩，故本次设计选取扭矩承载能力最强的双曲线形的膜盘型面，初步选取膜盘组件材料为42CrMo。

膜盘所受切应力理论计算公式为：

(1)

式中：r为膜盘任意点半径；ra为膜盘最薄处半径；d0为膜盘最薄处厚度；n为型面系数，对于双曲线n=2。

已知膜盘联轴器所承受的扭矩T=25.46 kN·m，取最薄点厚度d0和半径ra，分别计算其切应力数值，如表1所列。

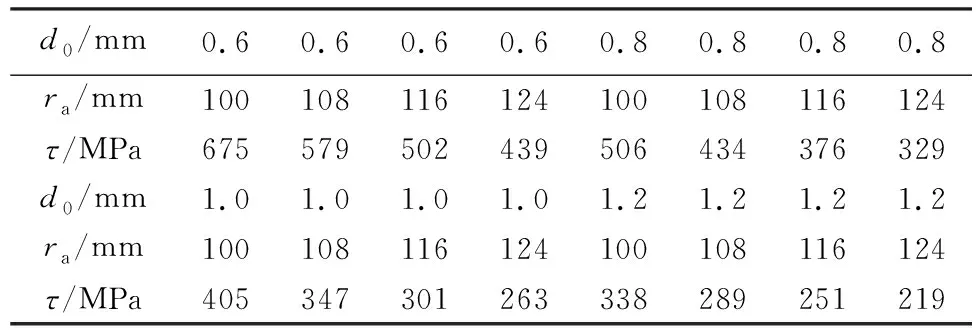
表1 不同型面厚度及半径剪应力

可以看出，膜盘型面越厚，膜盘受扭矩所产生的切应力越小，但型面越厚，膜盘刚度越大，其承受相同轴向、角向位移时所产生的应力越大；膜盘最薄处半径越大，膜盘受扭矩所产生的切应力以及轴向、角向位移所产生的应力都会变小。受限于对膜盘联轴器的大小要求，初步设计取膜盘型面最薄点厚度d0=1 mm，最薄点半径ra=116 mm，此时膜盘所受纯扭矩时的切应力τ=301.14 MPa。

膜盘型面内、外径比值(内半径指型线最厚点处半径，如图3中标注r=58 mm处；外半径指型线最薄点处半径，如图3中标注r=116 mm处)决定了膜盘型线的长度，这直接影响到膜盘的刚度及各项应力的大小及分布。通常，膜盘型线内、外半径比值取0.4～0.6，本次设计时选取内、外径比值为0.5。

膜盘联轴器与输入、输出轴传递扭矩是通过花键来实现的，设计时为了简化结构，便于加工，考虑膜盘与外花键设计为一体，同样选用花键材料为42CrMo，外花键的部分设计参数如表2所列，可得如图3所示的膜盘组件的截面示意图。

开展大学生思想政治教育工作是辅导员的核心工作，然而由于辅导员自身指导理论的有限性以及多重身份的局限性等因素，在一定程度了增加了其在思想政治教育工作中的难度。与此同时，信息网络化的普及、文化多样化的发展在一定程度上拓宽了大学生对思想政治教育内容的获取途径，也为辅导员话语权带来了诸多挑战。

表2 外花键参数表

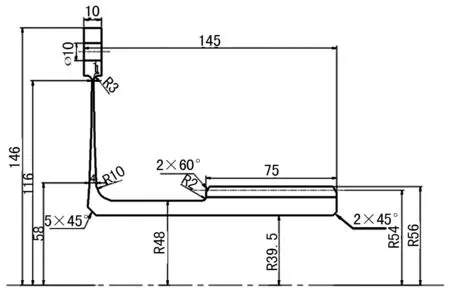
图3 膜盘联轴器膜盘组件截面图

1.2 螺栓及中间轴的设计

中间轴的设计采用圆柱形轴孔，同时为了增大膜盘联轴器的补偿能力，把中间轴两端同样设计膜盘，将中间轴通过螺栓与两侧的膜盘相连，选用其材料为42CrMo，中间轴与两边膜盘部分连接的截面示意图如图4所示。

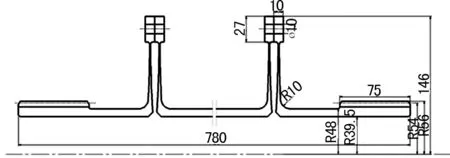
图4 膜盘联轴器截面图

膜盘联轴器的扭矩通过螺栓传递，因此螺栓选取至关重要，选取螺栓直径d=10 mm。初步选取螺栓材料为20CrMnTi。

选取GB/T 27-1988的M10铰制孔用螺栓，沿膜盘外环均匀分布18个，螺栓所受的剪力计算式为：

(2)

式中：T为转矩；rmax为最大半径；z为螺栓数目；ri为每个螺栓的半径。

计算可得每个螺栓所承受的力F=1.03×104N。螺栓杆的剪切强度为：

(3)

式中：F为螺栓承受的剪力；d0为螺栓剪切面的直径。

由此可计算出每个螺栓所承受的剪应力τ=131.14 MPa，故螺栓剪切强度满足要求。

1.3 膜盘联轴器整体模型

在ANSYS中对设计的膜盘联轴器模型进行建模，将膜盘组件与中间轴通过螺栓联接起来，由于膜盘联轴器的左右均是通过花键和其它部分连接，故在模型两端补充了内外花键与之啮合，得到膜盘联轴器三维实体模型如图5所示。

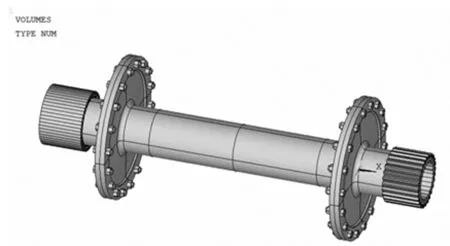
图5 膜盘联轴器整体模型

2 膜盘联轴器应力分析

由于整体计算时所需建立的接触对比较多，计算比较缓慢，为了简化分析，根据所设计膜盘联轴器结构左右对称这一特点，选取图5右端的部分为代表，对其进行有限元强度分析。

首先建立图6(a)所示的膜盘联轴器简化计算模型，分别对各构件设置不同材料参数，采用solid185六面体单元进行网格划分，得到膜盘联轴器的有限元网格如图6(b)所示，共计实体单元数286 552，节点数411 064。

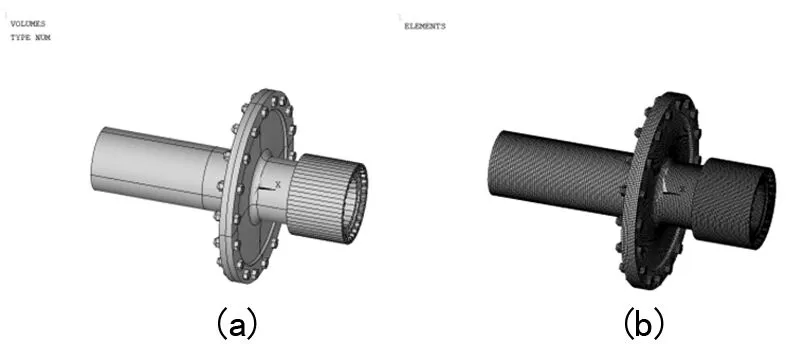
图6 膜盘联轴器有限元网格模型

2.1 扭矩作用下的膜盘应力

对有限元模型设置边界条件如下：①将大小为25.46 kN·m的扭矩转化为切向力施加到中间轴端面节点上；②右侧内外花键之间建立接触对，轴向挡圈与外花键之间建立接触对；③右侧内花键外圈表面施加零位移约束；④螺栓分别与膜盘、中心轴、太阳轮轴相粘结。可计算得到膜盘的等效应力云图如图7所示，图8给出了膜盘型面上的等效应力数值。

图7 膜盘等效应力云图 图8 膜盘型面部分位置等效应力

由图7可知，膜盘的等效应力最大值为763.665 MPa，出现在太阳轮轴与花键连接处，表现为应力集中。结合图8可以看出，膜盘型面上的等效应力均为536 MPa左右，符合双曲线型面在承受扭矩时型面上等强度的特点。

2.2 角向补偿作用下的膜盘应力

根据膜盘联轴器的角向补偿要求，膜盘联轴器需补偿最大0.33°的角向位移，故按照最大角向补偿量的0.33°来进行校核计算。因此设置边界条件如下：①将大小0.33°的角向位移施加到左侧中间轴端面的一列点上；②右侧内外花键之间建立接触对，轴向挡圈与外花键之间建立接触对；③螺栓分别与中间轴、膜盘、太阳轮轴相粘结；④右侧内花键外表面施加零位移约束。图9给出了膜盘的等效应力云图。

由图9可以看出，等效应力最大值为74.871 MPa，出现在膜盘型面顶部，其方向与角向偏移的方向一致。

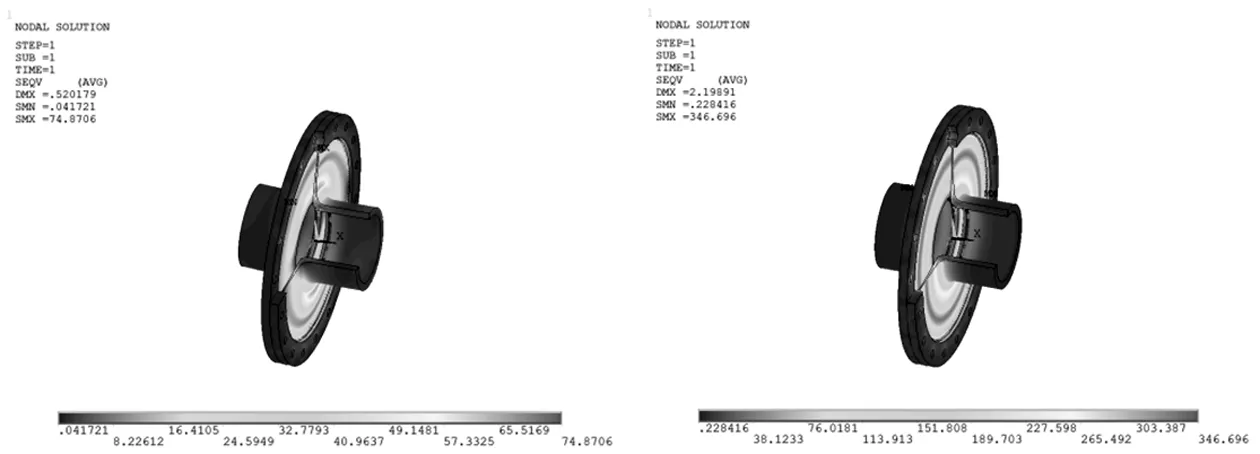
图9 膜盘等效应力云图 图10 膜盘等效应力云图

2.3 轴向作用下的膜盘应力

根据膜盘联轴器的轴向补偿要求，膜盘联轴器需补偿最大4.4 mm的轴向位移，由于联轴器整体左右对称，仅选取右侧一半进行计算，故按照最大轴向补偿量的一半2.2 mm来进行校核计算。因此，设置边界条件如下：①将大小2.2 mm的轴向位移施加到左侧中间轴的端面节点上；②右侧内外花键之间建立接触对，轴向挡圈与外花键之间建立接触对；③螺栓分别与中间轴、膜盘、太阳轮轴相粘结；④右侧内花键外表面施加零位移约束。图10给出了膜盘的等效应力云图。

由图10可以看出，膜盘等效应力最大值为346.696 MPa，出现在膜盘型面顶部，且型面顶部和底部一圈的应力均较大。

2.4 综合作用下的膜盘应力

膜盘联轴器在补偿轴向位移+角向位移时，同时还需要传递扭矩，故计算膜盘联轴器在承受角向位移+轴向位移+扭矩的情况。因此设置边界条件如下：①将角向位移、轴向位移所提取的节点力对应施加到左侧中间轴的对应节点上；②右侧内外花键之间建立接触对，轴向挡圈与外花键之间建立接触对；③螺栓分别与中间轴、膜盘、太阳轮轴相粘结；④右侧内花键外表面施加零位移约束；⑤将大小为25.46 kN·m的扭矩转化为切向力施加到中间轴端面节点上。图11给出了膜盘的等效应力云图。

由图11可以看出，膜盘等效应力最大值为818.688 MPa，出现在膜盘右侧太阳轮轴上靠近花键的位置，表现为应力集中，膜盘型面上应力较大处为型面顶部，其应力值为627 MPa左右。

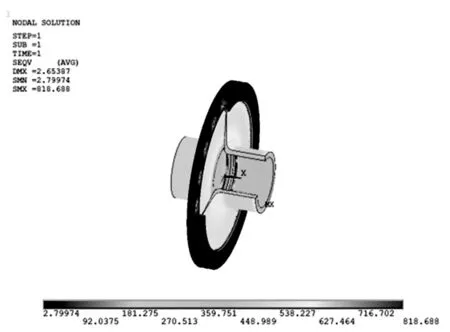
图11 膜盘等效应力云图

3 结 论

对大扭矩膜盘联轴器进行了设计及强度分析，结果表明：在大扭矩的情况下，双曲线型面膜盘具有良好的抗扭能力；针对补偿位移，膜盘应力最大值通常出现在型面的内侧或外侧过渡区域，轴向位移相比于角向位移产生的应力较大，但膜盘联轴器往往处于上述几种复合载荷的工作环境下，致使膜盘会产生更大的应力。为膜盘联轴器整体设计及优化提供重要参考。