基于浸入实体法的双涡轮液力变矩器流场仿真*
2020-08-05彭建涛林腾蛟刘嘉慧蒋仁科
彭建涛,林腾蛟,刘嘉慧,蒋仁科
(1.重庆大学机械传动国家重点实验室,重庆 400044; 2.广西柳工机械股份有限公司,广西 柳州 545007)
0 引 言
双涡轮液力变矩器是以液体为工作介质的一种非刚性扭矩变换器,是液力传动的一种形式,主要起到传递转矩、变矩以及离合作用,具有调节范围宽、起动变矩比大、高效区宽等优点,广泛应用于载重汽车、装载机、推土机等工程车辆[1]。双涡轮液力变矩器内部流动决定外部性能,开展其内部流动特性研究具有重要的理论意义及工程价值。
早期学者针对双涡轮液力变矩器的研究主要集中在流场数值模拟及台架试验分析。Habsieger等[2]研究了液力变矩器速比和质量流量间的关联规律,采用激光测速法测量了泵轮出口和涡轮入口平面的流速。Yuki等[3]比较不同循环圆液力变矩器之间的变矩性能,采用CFD分析了高扁平比液力变矩器的外特性。贾双林、石祥钟等[4-5]分别对D315型与YJSW315型双涡轮液力变矩器中的一涡及二涡的内部流场进行数值模拟分析,研究了两级涡轮流动状况对涡轮效率影响规律。随着计算机发展及计算方法不断成熟,流场计算逐渐由稳态发展到瞬态。Bois、Yamaguchi等[6-7]对液力变矩器进行瞬态流场分析,研究了局部流型和速度比的关系。刘春宝等[8]采用多流动区域耦合算法对液力变矩器瞬态控制方程进行计算,得到变矩器外部性能,并与试验作对比,验证了瞬态流场数值计算方法正确性。目前,关于双涡轮液力变矩器的瞬态流场仿真主要采用动网格法建立流体域计算模型,在进行复杂几何形状刚体在流体域内运动仿真时,大量的网格重构加大了计算机的计算成本。采用浸入实体法可有效减少网格重构带来的缺点,但少有学者采用该方法进行变矩器流场的数值仿真分析。
双涡轮液力变矩器的每个工作叶轮内流道结构复杂,叶片表面为复杂曲面,本文基于浸入实体法对图1所示双涡轮液力变矩器的内部流场进行数值仿真,运用该方法能便捷地分析变矩器内部全域流体动力学性能,研究其内部速度场和压力场分布规律。

图1 双涡轮液力变矩器结构示意图
1 浸入实体法基本原理
浸入实体法将动量源项施加在浸入实体区域内流体,驱动流体速度与固体速度相匹配[9]。建立流场计算域时需保证实体域完全浸没于流体域,同时不穿过任何流场边界或与其他固体间存在碰撞交叉。浸入实体法原理如图2所示,其中实线代表浸入实体边界,浸入实体边界点IB移动迫使流体域网格节点NW移动。

图2 浸入实体法原理
浸入实体法基本公式如下:
(1)
(2)
(3)
y*=max (y*,11.06)
(4)
u+=lny*/κ+C
(5)
(6)

2 模型建立及边界条件设置
2.1 计算域模型建立及网格划分
双涡轮液力变矩器主要工作元件为泵轮、一级涡轮、二级涡轮及导轮,其流体域模型及实体域模型如图3所示,其中四个工作叶轮的叶片为浸入实体域,建模时使其完全浸没在内流道流体域中。

图3 液力变矩流体域及实体域三维模型
根据双涡轮液力变矩器工作叶轮的结构参数,采用UG软件建立变矩器的流体域和固体域模型,而后将模型导入到ANSA中进行网格划分,液力变矩器内部流场网格如图4所示,其中流体域节点数为1 623 875,实体域节点数为563 592。

图4 叶轮内部流场网格
2.2 流场计算简化假定
双涡轮液力变矩器工作叶轮结构复杂,工作介质在内部的流动难以预测,在对其内部流场进行分析时,做出如下简化假定:
(1) 忽略变矩器工作叶轮叶片与工作介质的流固耦合作用,即将工作叶片及工作轮的内外环视为刚体,且各叶轮不产生轴向位移。
(2) 液力变矩器工作介质采用GB标准的液力传动油,其密度在工作过程变化很小,可视其密度为定值,即假设工作介质为不可压缩黏性流体。
(3) 液力变矩器运行过程中,忽略因对流换热、热辐射及机械能与内能转化等造成工作介质温度变化。
(4) 工作介质流经过两叶轮间无叶栅区时,忽略其泄漏问题,即上游叶轮出口端流出的油液全部进入下游叶轮。
2.3 边界条件设定
液力变矩器内部流场的流动是复杂的湍流问题,工作叶轮叶片旋转造成内流道压力差、流速差及空间容积变化,且流道内存在漩涡、回流等流动现象,因此内部流场计算选择RNGk-ε湍流模型,能获得较为真实的模拟结果。浸入实体法实体域及流体域网格均采用交错网格,因此压强速度耦合算法采用SIMPLE算法。流体介质为液力传动油,其密度为ρ=899.1 kg/m3,黏度为μ=0.001 89 Pa·s。仿真分析时叶轮实体网格按实际计算工况定义转动,其余边界均为壁面条件。浸入实体法计算流程如图5所示。
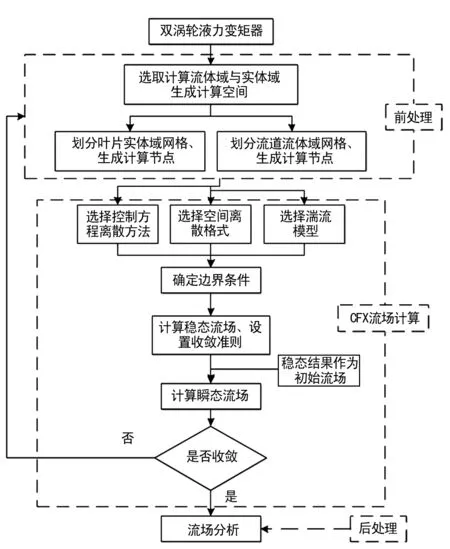
图5 浸入实体法计算流程
设置瞬态计算时间步为800步,计算总时长为0.6 s,步长为0.000 75 s,计算收敛条件为两次迭代残差小于10-4。液力变矩器瞬态流场计算采用全流道模型,上游叶轮出口端与下游叶轮进口端紧密相连,油液流动情况近似,但两叶轮转速不同,为了进行统一计算,采用混合平面理论,如图6所示。

图6 双涡轮液力变矩器混合平面
3 仿真结果分析
通过对给定边界条件的计算域进行数值仿真,分析液力变矩器变矩器泵轮、两级涡轮及导轮内部流场流动特性。经过160步计算后,进出口流量、动量残差均小于10-4,计算收敛。
3.1 泵轮流场分析
图7为泵轮流体域压力分布。泵轮转速较高,产生较大离心力。在离心力作用下,泵轮压力由泵轮入口向出口逐渐增大,泵轮入口靠近叶片非工作面存在局部低压区;从导轮流出的油液主要沿导轮叶片出口方向流入泵轮,冲击泵轮叶片吸力面,形成局部高速区域,并在进口附近产生涡流,如图8所示。

图7 泵轮压力分布

图8 泵轮速度矢量分布
3.2 一级涡轮流场分析
图9给出了一级涡轮流体域压力分布,其进口处压力高于出口处,外环压力高于内环,压力梯度变化较小。一级涡轮进口处流速较大,在靠近内环位置易产生脱流,影响涡轮效率;叶片出口速度分布呈现射流状态,且在靠近外环处出现较高速射流区,如图10所示。

图9 一级涡轮压力分布

图10 一级涡轮速度矢量分布
3.3 二级涡轮流场分析
二级涡轮内流道油液流速及压力略有提升,随着流动的深入,油液压力及速度逐渐减小,其外环压力高于内环压力;如图11所示。二级涡轮进口处速度梯度较大,工作面与外环相交处油液流速较大;油液流入流道后,速度逐渐减小,在流道叶片弯曲较大处易出现脱流,影响二级涡轮效率,如图12所示。

图11 二级涡轮压力分布

图12 二级涡轮速度矢量分布
3.4 导轮流场分析
导轮内流道压力分布如图13所示。导轮进口端工作油液压力较出口端压力大,油液在导轮外环叶片前端附近形成高压区。导轮流道内液体速度矢量在各个面上有较大差异,由于导轮叶片导向作用,工作油液流经导轮后流向发生改变,油液压力减小,但局部速度值增加,在导轮出口靠近外环处出现高速区,如图14所示。

图13 导轮压力分布

图14 导轮速度矢量分布
4 液力变矩器工作特性分析及试验验证
涡轮叶片受到工作油液高速冲击而获得转矩TT,如图15所示,液流作用于涡轮上的转矩为:

图15 涡轮进口及出口动量矩
TT=ρQ(vuT2rT2-vuT1rT1)
(7)
式中:Q为涡轮流道内流量;vuT1、vuT2为涡轮进口、出口处绝对速度的圆周分速度;rT1、rT2为涡轮进口、出口处半径。
涡轮进口、出口绝对速度在三维空间上可分解为牵连运动速度uT1、uT2与相对运动速度wT1、wT2,其中牵连运动速度计算式为:
(8)
式中:nT为涡轮转速。
由图16所示的涡轮入口及出口速度三角形可知,绝对速度的分速度计算式为:

图16 涡轮进口及出口速度三角
(9)
式中:βT1、βT2为涡轮进口角及出口角;vmT1、vmT2为涡轮进口和出口处轴面分速度。
轴面分速度vmT=Q/Am,式中Am为中间流线垂直的截面积,速度方向与涡轮叶片中间流线相切,其中流量Q及中间流线垂直截面积Am由变矩器三维流场数值仿真计算得出。
对于双涡轮液力变矩器而言,其主要特性参数包括变矩比K、泵轮扭矩系数λB及传动效率η。各特性参数计算公式如下:
(10)
(11)
η=K·i×100%
(12)
式中:T1为输入转矩,由发动机参数确定;T2为输出转矩;TB为泵轮转矩;g为重力加速度;nB为泵轮转速;D为变矩器循环圆有效直径。其中,泵轮转矩TB可参照涡轮转矩TT计算方法计算得出,输入转矩T1由发动机参数决定,输出转矩T2可由下式计算:
(13)
通过计算得到双涡轮液力变矩器特性计算曲线,与实测变矩器试验性能曲线对比,如图17所示。

图17 液力变矩器工作特性仿真与试验对比
由图可知,在i=0.1时数值计算与试验数据误差较大,而在其他工况下,两者在数值上及曲线趋势吻合良好,整体平均误差为10.58%,因此基于浸入实体法的双涡轮液力变矩器的流场数值分析具有较好准确性。
数值计算时假设工作介质完全由上游叶轮出口流入下游叶轮进口,忽略了两叶轮之间无叶栅区的泄漏问题,而实际上工作介质不可避免从间隙中上下游叶轮进出口间存在间隙流出,降低变矩器效率,因此仿真结果效率值比试验结果效率值略大;液力变矩器工作时,其内部不可避免存在气化现象,造成变矩器功率损失,而在数值计算时未能考虑这些因素,亦会产生仿真结果误差。
5 结 语
基于浸入实体法对双涡轮液力变矩器内流道压力、速度分布进行仿真分析,得到其内流道存在涡流、脱流等现象,降低了变矩器的工作效率。
通过液力变矩器外特性仿真结果与试验值对比,验证了浸入实体法仿真计算的准确性。采用浸入实体法进行流场计算,充分利用其网格优越性,为双涡轮液力变矩器流场计算提供便利。
