内燃机冷却水腔表面形貌对沸腾换热影响的研究

邱学军，白曙，侯刘闻迪

(1. 华域科尔本施密特活塞有限公司，上海 201814；2. 上海柴油机股份有限公司，上海 200438；3. 联合汽车电子有限公司，上海 201206；4. 江苏大学 汽车与交通工程学院，镇江 212013)

0 引言

国V、国六等低排放法规的出台，使作为汽车心脏的内燃机受到更广泛的关注[1]。缸盖和活塞顶部与气缸内壁共同构成内燃机的燃烧室，其工作环境极为恶劣，是内燃机中较为重要的散热部件。如果冷却效果不好，极易造成缸盖火力面出现开裂，所以改善缸盖冷却水腔的换热能力显得尤为重要。过冷流动沸腾换热作为一种新型内燃机冷却方式，逐渐受到广大学者的关注。目前，对内燃机缸盖冷却水腔的沸腾换热研究主要集中在不同流动参数和冷却介质对沸腾换热的影响及冷却水腔沸腾换热模型的建立等方面，较少涉及冷却水腔的表面形貌对沸腾换热的影响。但在核工业、微电子业、制冷业等对沸腾换热要求较高的行业，已有国外学者开展了一系列通过改变表面形貌来增强沸腾换热的研究，这些研究主要从表面粗糙度和人工形貌2个方面出发。在表面粗糙度方面，2013年，McHale等人基于汽泡脱离直径、生长时间、空泡份额等参数，比较传热系数和汽泡沸腾特性在相对不确定度上的关系[2]。结果表明，传热结果与表面面积比线性相关。2015年，Paz等人采用7种不同材料和粗糙度的加热表面进行了过冷流动沸腾试验[3]。结果表明，随着粗糙度的增加，热流密度随之增加。在人工形貌方面，2007年，Kuo等人在带有凹坑结构的微通道中进行了流动沸腾试验，在不同质量流速和热流密度下，对流动形态、沸腾初始时间、换热系数和临界热流密度进行研究[4]。通过与平壁微通道的比较发现，带凹坑结构的通道能够促进汽泡成核，提高临界热流密度，使汽泡成核的再生性和均匀性更好。2016年，Jafari等人模拟了微通道内单个人造凹坑表面上汽泡从凹坑中生长到脱离的整个过程[5]。模拟结果展示了通道中的速度、温度和压力场分布，表明带凹坑的表面相比于光滑平面能够提高8倍的沸腾换热能力。综上所述，在对流换热方面，表面形貌能够大幅增加换热面积，促进周围流体的扰动，增强对流换热；在沸腾换热方面，表面形貌能够改善受热表面流体流动状况，促进汽泡成核、生长、聚合、脱离等演化行为，加强沸腾换热。因此，深入探究表面形貌对于内燃机冷却水腔内沸腾换热的影响具有重要的现实意义。

基于此，本文建立了适用于高强化内燃机工况的高精度沸腾换热计算模型，并以矩形通道为对象，在冷却流道上布置不同表面形貌，从热流密度、空泡份额和流速方面来探究表面形貌强化沸腾换热的规律和机理。

1 模型介绍

沸腾换热在核工业、微电子业等工程领域应用较广，但复杂的流动和传热特性及其中的相变问题，使其在内燃机领域的应用受到限制。因此，深刻理解沸腾换热机理、气泡动力学理论，选用合适的计算流体动力学(computational fluid dynamics, CFD)软件和数值计算模型对开展内燃机中的沸腾换热研究至关重要。本文选取了数值计算所需的VOF(Volume of fluid)模型、壁面沸腾模型、湍流模型和质量传递模型，用于分析冷却水腔内不同形貌的传热特性，为提高内燃机冷却系统性能奠定理论基础。

1.1 VOF模型

在VOF模型中，气液相界面的位置由每相控制单元的体积分数确定。其中，每相控制单元中液相和气相的体积分数分别为αL和αV，它们的和为1[6]。

混合相的密度、黏度和热导率基于两相的体积分数来计算，其公式如下：

ρ=αLρL+αVρV

(1)

μ=αLμL+αVμV

(2)

k=αLkL+αVkV

(3)

式中：ρ、ρL、ρV分别为混合相、液相和气相的密度，kg/m3；μ、μL、μV分别为混合相、液相和气相的动力黏度，kg/(m·s)；k、kL、kV分别为混合相、液相和气相的热导率，W/(m·K)。

结合式(1)～(3)，可得连续性方程如下：

(4)

(5)

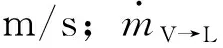
VOF模型中的动量方程为：

(6)

式中：p为相对压力矢量，Pa；T为温度，℃；FV为体积力，N，表示单位体积所受的表面张力。

气液两相的能量方程为：

(7)

式中：E为质量能量，kg/s；SE为气液发生相变时的能量源，W/m3。

另外，在VOF模型中将单位质量的能量E定义如下：

(8)

式中：EL和EV分别为液气两相的能量，kg/s，由各相的比热以及共同温度决定。

1.2 质量传递模型

本文采用Lee提出的传热传质模型[7]进行数值模拟。该模型充分考虑了近壁面和主流区的相变，将相变流体的温度分布维持在合理范围中。相变质量传递主要根据流体温度和饱和温度来确定，传递的质量为：

当TF≥Tsat时，液相开始蒸发，质量从液相转移到气相。质量传递如下：

(9)

当TF≤Tsat时，气相开始冷凝，质量从气相转移到液相。质量传递如下：

(10)

当质量源确定之后，两相间传递的能量为相间的质量传递速率和汽化潜热的乘积。

1.3 壁面沸腾模型

本文在VOF模型基础上，采用Rohsenow壁面沸腾模型[8]计算加热面上的沸腾热流密度。沸腾发生时，总热流密度为：

(11)

式中：qtotal为壁面沸腾换热的总热流密度，kW/m2；qC为对流换热热流密度，kW/m2；qB为核态沸腾热流密度，kW/m2；qI为到达沸腾起始点所消耗的热流密度，kW/m2。其中qC、qB和qI的公式为：

(12)

(13)

(14)

式中：TW、TW,I和TP分别为壁面温度、沸腾初始时的壁面温度和近壁面节点P处的温度，℃；T*为对数律的无量纲温度；Cp,L为液体比热容，J/(kg·K)；Cμ为湍流经验常数；Csf为液体与加热表面间的特性常数，由加热表面和流体的材料性质来确定；kP、kL分别为近壁面节点P处和液体的湍动能，J；hH,L为液体汽化潜热，J/kg；PrL为液体普朗特数；σl为相界面所受的表面张力，N。

1.4 湍流模型及壁面函数

采用雷诺时均模拟方法，平均化处理不同时间流场的各项物理参数，并求解时均化控制方程。本文冷却流道中的湍流运动通过标准k-ε模型来计算，其表达式为[9]：

(15)

(16)

(17)

式中：k为湍动能，J；ε为湍流扩散率，%；μt为湍流黏度，kg/(m·s)；σk、σε、C1、C2、C3和Cμ都是湍流经验常数，其值分别为1、1.3、1.44、1.92、0和0.09。

2 冷却流道模型建立及数值求解

2.1 几何模型

参照刘永丰试验中模拟冷却水腔矩形流道[10]，设置与其流道尺寸和加热面尺寸都相同的几何模型，通过比较不同工况下的计算结果与试验结果，验证该沸腾模型的准确性。

该模型的几何尺寸如图1所示。矩形流道的总长为500 mm，宽为26 mm，高为14 mm；加热区长为94 mm，宽为18 mm；加热面布置在距离进口308 mm、出口98 mm的位置处，该位置距离进口超过了10倍水力直径，可以使湍流运动充分发展，也可以减少二次流动对汽泡脱离造成的影响，从而提高计算精度。

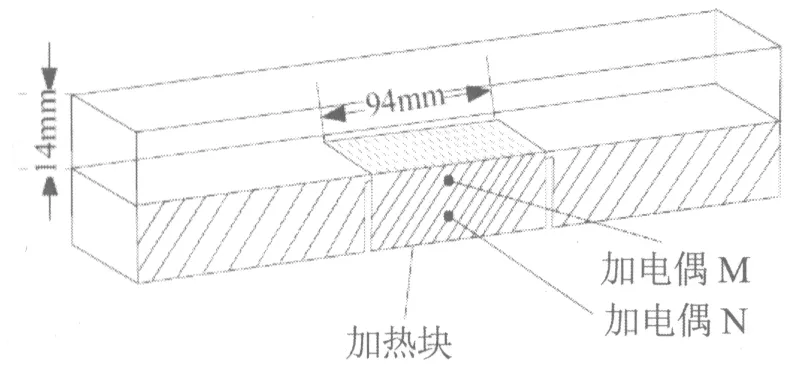
图1 试验流道几何模型

本文设计了4种形貌。设计方案时，考虑到加热面尺寸和网格划分要求，尽可能减小对冷却流道结构强度的影响，又考虑到实际的计算时间有限，最终确定形貌间流向间距a为12.00 mm，横向间距b为3.00 mm，加热区共15个形貌点如图2所示。

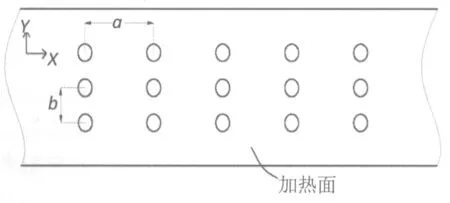
图2 冷却流道形貌间距参数

4种形貌包括圆柱形凹坑、圆柱形凸起、半球形凹坑和圆台形凹坑，同时保证每种形貌的表面积和总个数相同，每种形貌的具体尺寸如图3所示。

图3 不同形貌的示意图

2.2 边界条件与计算工况

气液两相分别设为水和水蒸气，对应的体积分数为0和1，设置为连续相和离散相。在不同的饱和压力下，水和水蒸气的物性参数会发生变化，本文采用IAPWS-IF97的公式[11]进行计算。为了模拟内燃机水腔中流体的受热和流动状况，在进口给定流速和温度边界条件，在出口给定相对压力边界条件，系统压力通过改变气液两相的物性来控制，加热面给定均匀温度边界，剩余壁面设为绝热壁面，所有壁面都设为无滑移壁面，如图4所示。

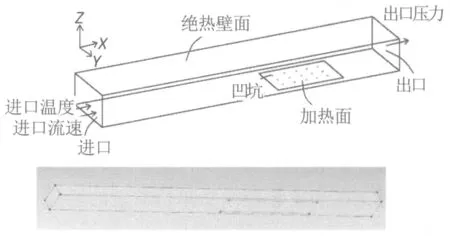
图4 模拟通道

选取部分内燃机工况作为本文的计算工况，通过计算加热面的热流密度来反应沸腾换热的剧烈程度，并将其与试验值进行比较，以验证沸腾模型精确性。计算工况如表1所示。

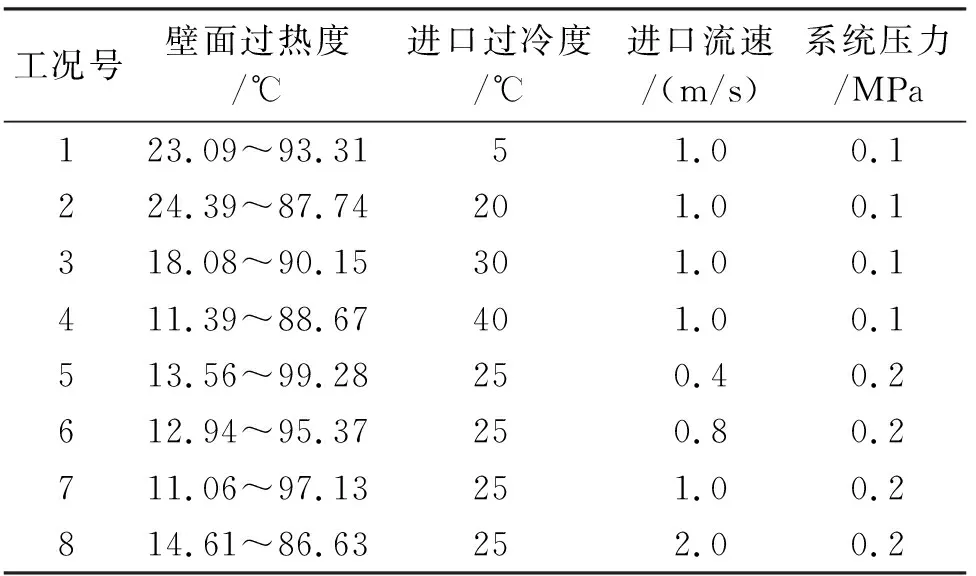
表1 计算工况

表中壁面过热度ΔTsup和进口过冷度ΔTsub的计算公式如下：

ΔTsup=TW-Tsat

(18)

ΔTsub=Tsat-Tinlet

(19)

式中：Tw和Tinlet分别为加热面壁面温度和进口温度，℃。

2.3 网格无关性验证

本文采用时间导数项的一阶隐式格式来进行瞬态模拟，采用SIMPLEC压力-速度耦合算法修正相邻和倾斜网格，采用2阶差分法来求解动量、能量和k-ε方程，表面张力则采用与温度相关的修正模型[12]进行计算。

本文使用非结构化网格来划分几何模型。在SC/Tetra中，使用的非结构化网格一般为四面体网格。选取的工况为过热度28 ℃、过冷度5 ℃、流速1 m/s、压力0.1 MPa，β值则采用SCT默认的100 s-1。计算结果如图5所示。当网格尺寸为1 mm时，计算的热流密度基本不变，因此选取整体网格尺寸1 mm的方案。另外，此网格方案的近壁面yplus数大于30，满足高雷诺数标准k-ε模型对于yplus的要求。yplus为无量纲数，用于判断边界层网格厚度是否落在黏性底层。

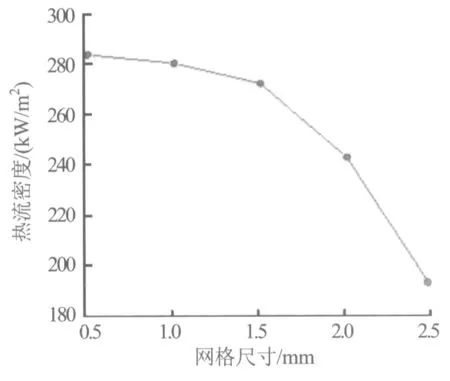
图5 网格无关性测试

3 计算结果与分析

3.1 不同表面形貌热流密度对比

为了寻找最有利于冷却流道换热的形貌，比较不同表面形貌对对流换热和沸腾换热的影响。 图6展示了不同工况下4种表面形貌上的热流密度计算结果。其中(a)和(b)计算工况为压力0.1 MPa、流速1.0 m/s的不同过冷度工况，(c)和(d)计算工况为压力0.2 MPa、过冷度25 ℃的不同流速工况。首先，比较光滑平面，在所有工况下4种形貌都有更好的换热效果。其次，对于低过冷度和低流速工况，随着过热度的增大，热流密度也随之增大，表明此时的主要换热方式由对流换热向沸腾换热过渡。圆柱形凸起的热流密度最大且其上升最快，说明圆柱形凸起强化沸腾换热的能力最强，其次是圆柱形凹坑和圆台形凹坑，半球形凹坑强化沸腾能力较差，主要换热方式仍为对流换热。最后，对于高过冷度和高流速工况，圆柱形凸起强化对流换热的作用最明显，圆柱形凹坑次之，半球形凹坑强化对流换热的能力优于圆台形凹坑。不同形貌的热流密度随过热度增加基本呈线性增长，表明在过冷度和流速较大时主要换热方式仍为对流换热。

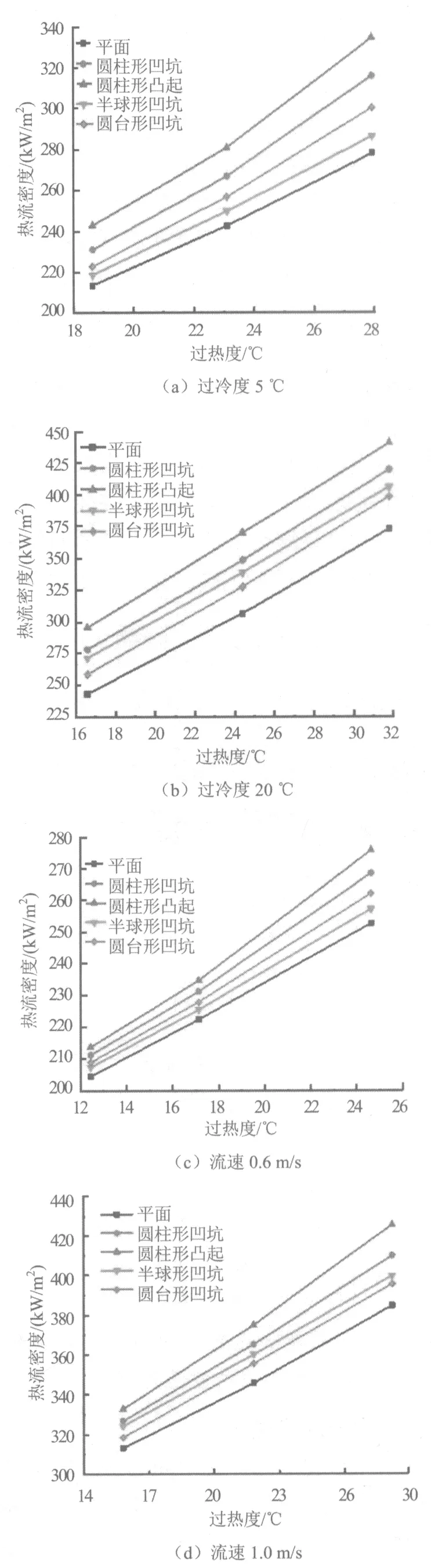
图6 不同表面形貌在不同工况下的换热特性比较

3.2 不同表面形貌空泡份额对比

通过比较不同形貌上的气相分布来探究不同形貌强化沸腾的差异。图7(a)为沸腾稳定时，在压力0.1 MPa、流速1.0 m/s、过冷度5 ℃、过热度23 ℃工况下计算得到的不同形貌加热面上的气相分布。圆柱形凸起和圆柱形凹坑加热面上的整体空泡份额较高，圆台形凹坑和半球形凹坑的空泡份额相对较少。此外，不同形貌上生成的汽泡大都集中在形貌周围，其中不同凹坑形貌的汽泡主要分布在凹坑正上方；而凸起形貌虽然其正上方的汽泡数量较少，但其带动周围平面区域汽泡成核和生长，使平面部分的汽泡数量明显较高。图7(b)为不同表面形貌加热面沿流向不同位置处的平均空泡份额，可见不同形貌的平均空泡份额整体都呈增大趋势。对于凹坑形貌，汽化核心更倾向于分布在凹坑底部的狭窄区域，在凹坑位置处出现平均空泡份额极大值，凹坑间的平面位置出现极小值；对于凸起形貌，在凸起位置处的平均空泡份额较小，凸起间平面上的平均空泡份额明显大于凹坑间的平面，整体空泡份额较大。原因是相邻凸起使加热面变得更加狭窄，凸起底角与周围平面生成的汽泡更易生长和聚合，汽泡脱离频率增加，强化沸腾换热。由图3可知，圆柱形凹坑底面的狭窄区域最广，有利于汽泡成核，其次是圆台形凹坑，半球形凹坑内部较为平整、光滑，不利于成核，沸腾换热效果差。

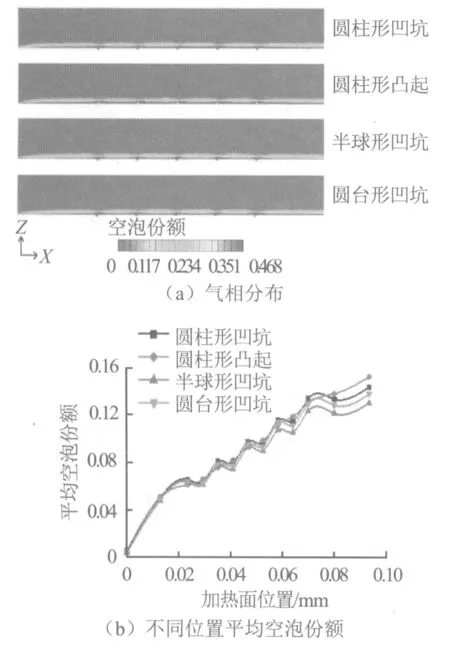
图7 不同形貌加热面上方的气相分布和沿流向平均空泡份额

3.3 不同表面形貌流速对比

选取不同形貌加热面正中间的一个凹坑或凸起作为对象，研究不同形貌局部的流速分布和流速矢量，结果如图8所示。对于凸起形貌，在凸起的前端和后端分布着范围较广的低流速区域，有利于汽泡成核、生长等演化行为；在凸起顶端受到流体的直接冲刷，该区域流速明显较大，汽化核心密度较小。因此，凸起顶部生成的汽泡数量较少，但在2个底角及周围平面上分布着大量汽泡。对于凹坑形貌，凹坑内部的流速明显小于凹坑外的主流区，其中圆柱形凹坑内部的低流速区范围较广，表明受流体的冲刷程度较轻，凹坑底角汽化核心密度大，有利于汽泡成核；圆台形凹坑内部的低流速区范围次之。而半球形凹坑内部低流速区范围较小，流体能够迅速冲刷整个半球壁面，不利于汽泡成核，成核密度较小；但半球形凹坑上方容易形成湍流，流速较大，有利于强化对流换热。

图8 不同形貌局部流速分布和矢量

图9为加热面上方0.4 mm位置处不同形貌近壁面沿流向的流速对比。对于凹坑形貌，近壁面流速沿流向都呈现增大的趋势。其中半球形凹坑的近壁面流速较大，其次是圆台形凹坑，圆柱形凹坑的近壁面流速最小。其原因是半球形凹坑较为光滑，内部漩涡中心靠近主流区，流体能够快速流出凹坑，所受阻力较小。而圆柱形凹坑狭窄、封闭，漩涡中心离主流区较远，不易带出流入凹坑底部的流体，流体流经凹坑所受阻力较大。圆台形凹坑介于两者之间，流体所受阻力适中。对于凸起形貌，近壁面整体流速低于不同凹坑形貌，说明流体流经凸起时所受的阻力远大于不同凹坑形貌，流体经过凸起时流速会大幅下降。如图9所示，在凸起后端有大片的低速涡流区，有利于周围平面汽泡的成核、生长等演化行为，强化沸腾换热。

图9 不同形貌加热面近壁面沿流向的流速

4 结论

本文分别在光滑和不同表面形貌的冷却流道内开展内燃机典型工况下的沸腾换热模拟研究，基于热流密度、空泡份额、流速等这些参数对不同表面形貌强化沸腾换热机理进行了深入探索，得到的结论总结如下：

1)圆柱形凸起主流区的流速最大、扰动最强，其次是圆柱形凹坑，因此圆柱形凸起强化沸腾换热和对流换热的效果最好，其次是圆柱形凹坑。半球形凹坑主流区的流速高于圆台形凹坑，因此圆台形凹坑强化沸腾换热的效果好于半球形凹坑，但强化对流换热的效果比半球形凹坑差。

2)对于凸起形貌，其前后端的低流速区域范围较广，促进汽泡成核，凸起间平面上的平均空泡份额明显大于凹坑间的平面，凸起的整体空泡份额最大；而在凸起顶端流速明显较大，抑制汽泡成核，在凸起位置处的平均空泡份额较小。流体经过凸起时受到的阻力最大，其近壁面的整体流速最低，最有利于强化沸腾换热。

3)对于不同凹坑形貌，汽化核心更倾向于分布在凹坑底部的狭窄区域，因为凹坑内部的流速远小于凹坑外的主流区，其中圆柱形凹坑内部的低流速区范围较广，流体冲刷程度较轻，有利于成核，圆台形凹坑次之；而半球形凹坑内部较为平整，低流速区范围较小，流体迅速冲刷半球壁面，不利于汽泡成核，但其上方容易形成湍流，扰动剧烈，有利于强化对流换热。