变速箱串联齿轮传动模态分析与有限元仿真*

王胜曼，唐宇恒

(1.保定理工学院，河北 保定 071000； 2.河北省地矿局第一地质大队，河北 邯郸 056000 )

0 引 言

对于齿轮传动系统，在刚性机械系统的动力学分析中，假设所有构件都是刚体。但是随着机械运动速度的提高，机械本身重量的减轻和机械工作精度的提高，构件本身的弹性变形成为不可忽略的因素。构件的弹性可以引起运动配合关系失调、降低运动精度、产生机械振动和机件疲劳损坏。在齿轮传动系统中当传动轴的长度比较大时，由于轴的弹性变形在机械起动、停车或载荷变化时会出现同一轴上零件运动的不同步或振动现象，从而影响机械的正常工作。因此整个齿轮传动系统的弹性问题在运行中产生的振动和精度问题是机械系统动力学研究的重点问题。

为了保证变速箱齿轮传动系统的运转精度减少振动，近年来不少学者针对此问题展开了机械系统动力学研究。一些学者利用不同的软件或者实验方法对其变速箱箱体进行了自由模态或约束模态的动力学仿真，其目的是为了改进箱体的结构设计以便减轻振动[1-7]。还有一些学者把齿轮传动系统中的一对齿轮啮合作为研究对象，利用ANSYS或其他软件进行模态分析，其目的是改善齿轮传动产生的振动和噪声[8-10]。还有一些学者把齿轮传动及变速箱壳体装配在一起作为研究对象，进行整体结构的模态分析，从而提出改进箱体整体结构的建议，以便减轻机械传动系统的振动问题[11]。以上这些研究只限于齿轮传动系统的部分构件的研究，只分析了部分构件的振动特性，没有对整个齿轮传动系统进行研究。

冯宇晨,陈艳锋撰写的行星齿轮传动系统接触模态分析一文中，作者对行星齿轮传动进行了自由模态和约束条件下两种模态仿真分析，获得了行星齿轮系统相应的固有频率和振型[12]。樊智敏撰写的带式啮合介质齿轮传动的模态分析一文中，把普通渐开线齿轮传动系统和带式啮合介质齿轮传动作为研究对象进行模态分析，并对比了两种仿真结果，发现改变介质带的弹性模量、泊松比、厚度等可以改变系统的振型[13]。基于Abaquas的齿轮传动系统模态分析一文中，将系统结构进行离散，使无限自由度问题简化成多自由度问题。建立了多自由度系统振动的运动微分方程，并利用利用Abaquas软件对变速箱进行了模态分析[14]。以上研究中研究者大都基于刚性机械系统多自由度动力学理论，采用了不同的研究工具，针对齿轮传动系统进行机械系统动力学分析，得出来系统的模态振型。但是对于齿轮传动系统中把轴类构件看作弹性构件进行扭转动力学系统分析的较少。

1 研究理论基础

1.1 串联齿轮传动系统等效力学模型

对于由N个轴组成的多级串联齿轮传动系统，利用拉格朗日方程可以简化成一单轴系统。

(1) 串联齿轮传动系统原始参数

如图1所示，已知J1,J2,J2′,J3,J3′,J4分别为转盘的转动惯量，θ1,θ2,θ2′,θ3,θ3′,θ4分别为转盘的转角，K1,K2,K3分别为轴的刚度系数。

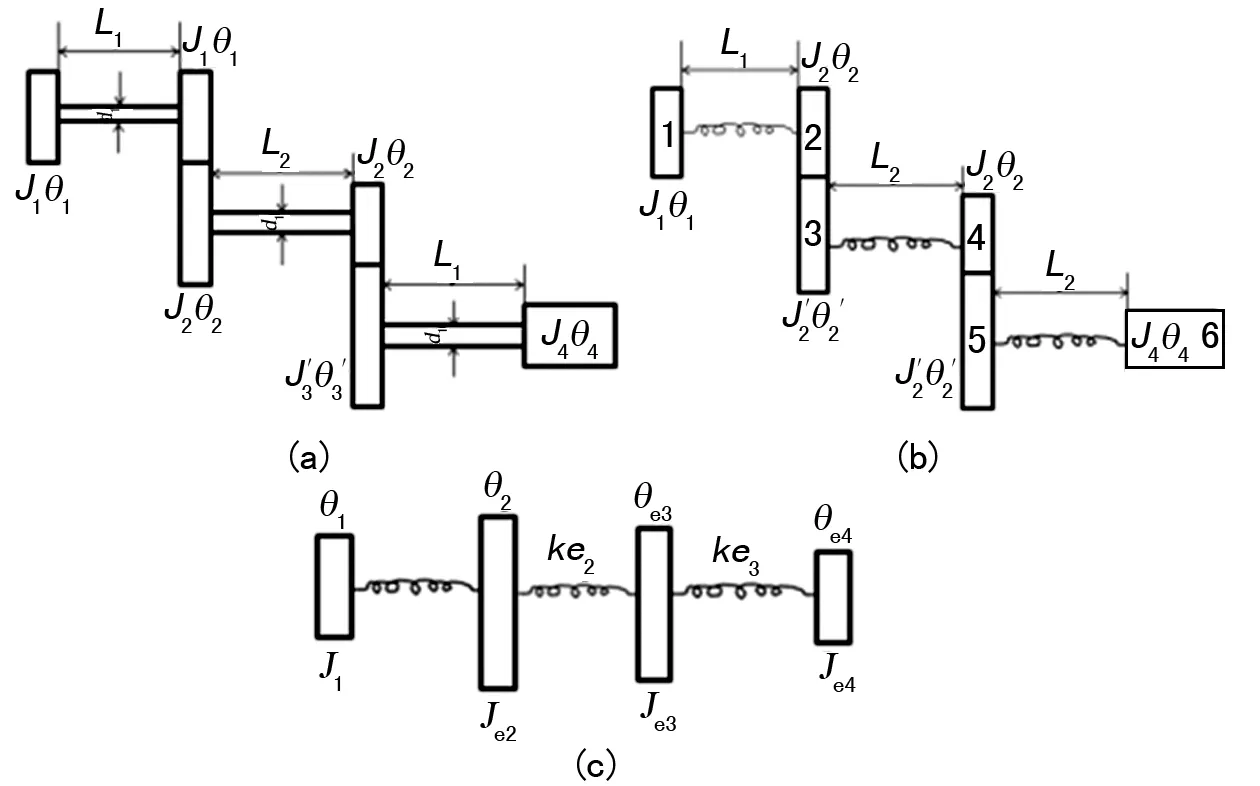
图1 传动系统简化力学模型

对于等截面轴，转角θ、刚度系数K可以采用材料力学中的计算公式进行计算求解。

式中：T为轴的扭矩；L为轴的长度；d为轴的直径；G为剪切模量；I为极惯性矩[15]。

(2)串联齿轮传动系统广义坐标

6.牛流行热。急性死亡多因窒息所致。剖检可见气管和支气管黏膜充血和点状出血，黏膜肿胀，气管内充满大量泡沫粘液。

根据图1(a)所示，θ2和θ2′,θ3和θ3′之间有确定的速比关系：

θ2′=i2′2θ2=i31θ1

θ3′=i3′3θ3=i43θ3

因此θ1,θ2,θ3,θ4相互独立为广义坐标，系统的自由度为4。

1.2 串联齿轮传动系统动力学方程

采用拉格朗日方程来建立系统的动力学方程。具有完整理想约束的有N个广义坐标系统的拉格朗日方程的形式是：

(1)

式中：E为系统动能；U为系统的势能；qr为第r个广义坐标；Fr为第r个广义坐标的广义力[16]。

系统的动能：

E对个参数求偏导数得：

(2)

系统的势能：

势能U对各参数求偏导数得：

=-i2′2K2θ2+(K2+K3i3′3)θ3-i3′3K3θ4

(3)

将公式(2)和公式(3)带入公式(1)中可得：

i3′3K3θ4=0

(4)

对公式(4)广义坐标进行变换，并进行参数替换得：

(5)

公式(5)为无外力时的动力学方程，图1(a)和(c)两个系统具有相同的动能和势能。

2 串联齿轮传动系统三维模型的建立

2.1 串联齿轮传动系统各构件的参数

如图1(a)所示，串联齿轮传动系统由带轮1、齿轮2、齿轮3、齿轮4、齿轮5、滚筒和轴1、轴2、轴3组成。各构件的原始参数见表1、表2所列。

表1 各轮参数表

表2 各轴参数

2.2 串联齿轮传动系统各构件材料特性

为了便于分析，串联齿轮传动系统各构件均采用优质碳素钢45，45号钢为中碳钢，含碳量为0.45%，一般用于比较重要的机械零部件的材料。见表3所列。

表3 构件材料特性

2.3 模型的建立和网格的划分

在建模环境下利用UGNX软件，建立串联齿轮传动系统各构件的三维模型。模型完成后在装配环境下，利用接触、对齐、距离、平行等约束等命令，对串联齿轮系统各构件进行约束。带轮与轴1、齿轮2与轴1、齿轮3与轴2、齿轮4与轴轴2、齿轮5与轴3、滚轮与轴3之间的装配采用接触与对齐进行约束；齿轮2与齿轮3、齿轮4与齿轮之间采用接触、对其、中心距离进行约束，从而完成串联齿轮传动系统的装配工作。在高级仿真环境下，利用NX NASTRAN求解器进行求解。NX NASTRAN求解器模态分析用于计算和评估结构的固有频率和自然模态即阵型分析，计算时不考虑阻尼，和外载荷也不相关。它提供了跟踪法、变换法和兰索士法3种数值解算方法。设置各构件材料属性，并指派对应材料。创建物理属性为PSOLID1，网格收集器为SOLID1，单元属性CTETRA10四面体网格。采用自由网格划分，单元大小为11.5 mm，单元总数为71 574个。有限元模型如图1所示，仿真模型如图2所示。

图2 串联齿轮传动系统三维装配模型 图3 串联齿轮传动系统有限元模型

3 仿真结果

文中分别对齿轮串联传动系统，采取自由模态进行计算和约束模态进行计算。自由模态仿真对象类型分别采用面对面粘接和面对面接触两种方案进行仿真计算。

3.1 串联齿轮传动自由模态计算结果

解算方案类型为SEMODES-103，子工况特征值法。特征值方法采用Lanczos法，所需数据模态数设置为14。仿真对象类型为面对面粘接，搜索距离为1mm，共创建17个面对。在无约束下状态下进行模态仿真。在[后处理导航器]窗口中，可以发现仿真计算结果的前6阶模态非常接近零，因为本次计算的是齿轮系统的自由模态，放开了6个自由度，在6个自由度方向中出现了刚体位移。仿真结果如表4和表5所列，串联齿轮传动系统非零后8阶模态见图4所示。

表4 非零后6阶模态频率及振型

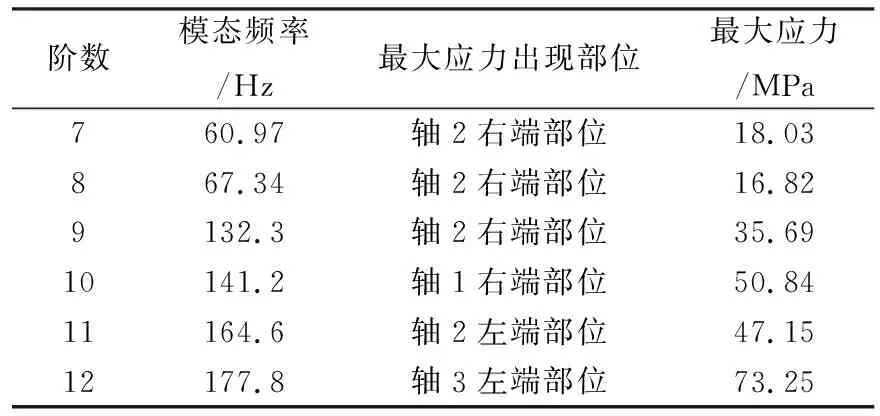
表5 非零后6阶模态频率及最大应力

图4 串联齿轮传动系统非零后8阶模态

从以上仿真数据可以看出，轴1、轴2、轴3的刚度严重不足，在各阶振型下发生了较大变形，且在各轴端部应力最大。如果激励频率与系统固有频率接近时发生共振，各轴将是最薄弱环节。同时各轴的较大变形，将严重影响系统的运转精度。因此在轴的端部施加支座或增加质量，将改善轴的振型，提高系统的稳定性。

3.2 串联齿轮传动等效模型模态计算结果

根据等效模型力学公式进行计算各轴的等效刚度和各轮的等效转动惯量，并将等效刚度进行逆运算，在各轴长度不变的情况下，等效为各轴的直径尺寸(见表6所示)。将等效转动惯量按照逆运算，在各轮宽度尺寸不变得情况下，等效为各轮的直径。(见表7所示)根据表6和表7中的尺寸，在UG建模环境下进行三维模型的建立并完成装配。在高级仿真环境中，设置各构件材料属性，材料同上，并指派对应材料。创建物理属性为PSOLID1，网格收集器为SOLID1，单元属性CTETRA10四面体网格。采用自由网格划分，单元大小为19.8 mm。解算方案类型为SEMODES-103，子工况特征值法。特征值方法采用Lanczos法，所需数据模态数设置为12。仿真对象类型为面对面接触，搜索距离为1 mm，共创建10个面对。在无约束下状态下进行模态仿真。在[后处理导航器]窗口中，查看非零后6阶模态频率及振型，见图6所示。仿真结果见表8和表9所列。

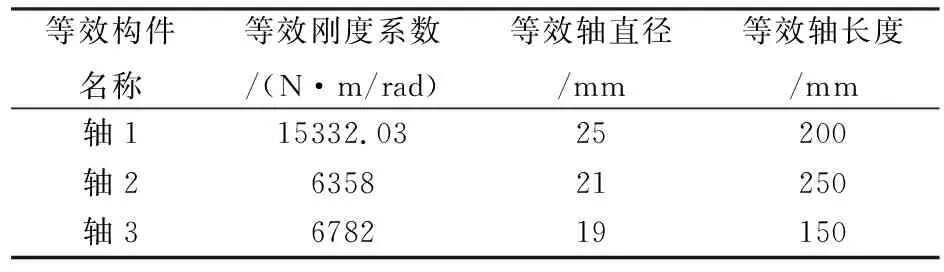
表6 等效模型各轴参数

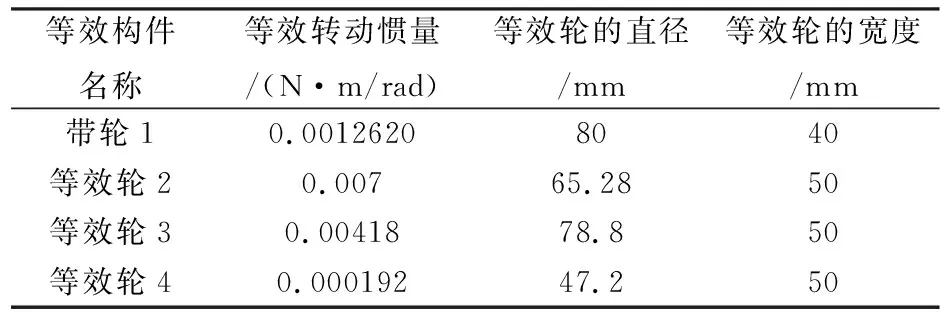
表7 等效模型各轮参数

表8 两种模型非零后6阶自由模态频率、最大变形量及最大应力数值表

图5 两模型前6阶振动频率

图6 两模型前6阶最大变形量

通过表8中的数据可以得出，原模型自由模态数据和等效模型自由模态数据在非零后前2阶振型频率非常接近。原模型第7阶模态频率为67.97 Hz，等效模型第7阶模态频率为67.89 Hz。原模型第8阶模态频率为67.34 Hz，等效模型第8阶模态频率为67.89 Hz。这两阶自由模态数据与研究理论相符。从第9阶开始，原模型模态频率与等效模型模态频率，开始出现差异。第12阶原模型模态频率远远低于等效模型模态频率，仿真结果与研究理论出现偏差。

4 分析与讨论

在进行串联齿轮传动动力学理论研究时，对系统进行了简化。

(1) 系统忽略了轴的质量，将轴看看成无质量的扭簧。实际中轴的几何尺寸越大，轴的质量也越大，轴的转动惯量也越大。因轴的质量被忽略，因此对振型产生了影响，影响了计算精度。

(2) 系统模型认为支撑是刚性的，不考虑轴的弯曲变形和纵向变形。本文进行了串联齿轮传动系统的自由模态分析，没有对各构件进行约束限制，因此在仿真的过程中，轴的弯曲变形或纵向变形对仿真结果产生了一定的影响。

(3) 系统模型忽略了传动机构内部的弹性，将各轴之间的传动比看作常数。实际中齿轮之间的啮合传动，在啮合面上因齿面受力作用，会发生一定范围内的弹性变形。在系统简化中将其看作刚体，实际仿真结果与研究理论有一定的差距。

5 结 论

本文首先利用拉格朗日方程对对串联齿轮传动系统进行了机械系统动力学模型的建立和理论计算，并将其原模型转化为等效系统模型。为了验证理论的正确性，笔者利用UGNX软件对其原模型和三维模型分别建模并装配，在高级仿真环境下进行仿真运算。并将两者结果进行比较，发现非零后前2阶即第7阶和第8阶两者自由模态振型和频率一致，符合研究理论。后四阶两者振型频率有一定的误差。此研究结论为齿轮传动系统振动分析与研究提供了理论参考。