纵有万变 殊途寻归——一道圆习题的变式教学课例

广东省惠州市惠阳区崇雅实验学校 李志平 欧阳卫彪

变式教学在初中数学教学中有着非常重要的作用，属于一种教学方式，在教学过程中应用这一方式，就能将数学中所存在的一些问题、各项条件进行转换，比如问题的形式、内容、条件等要素，这样就能够让学生养成多角度思考问题的习惯，最大程度地提高学生思维的灵活性，使其解决问题的能力得到有效的提升。以下以一道课本圆习题为例说明几何题变式教学的一般过程。

一、 变式教学过程

（一）原题导入

1.原题出处：新人教版《数学》教材九年级上册 P123 复习题6：如图1，大半圆中有n个半径相等的小半圆，大半圆的弧长为L1，n个小半圆的弧长和为L2，探索L1和L2的关系并证明你的结论。

2.背景分析：此题在学生学习了圆的弧长及周长公式的基础上，考查学生对圆弧长及周长公式的理解与灵活掌握。

（二）原题探析

1.思路分析：大圆的半径实际上等于小圆的半径之和，所以都乘π 之后，大圆的弧长等于小圆的弧长之和。

2.解题过程：L1=L2。理由如下：设n个小圆半径依次为r1，r2，…，rn，则大圆半径为r1+r2+…+rn，L2=πr1+πr2+…+πrn=π（r1+r2+…+rn）=L1。

3.考点分析：此题考查了圆的弧长公式及周长公式，运用总量等于各分量之和的数学思想。

（三）变式拓展

【变式1】如图2，大半圆中有n个小半圆（每个小半圆半径不同），大半圆的弧长为L1，n个小半圆的弧长为L2，探索L1和L2的关系并证明你的结论。

1.思路分析：虽然每个小半圆的半径不同，但是依然不改变总量等于各分量之和，也就是说大圆的半径实际上等于各小圆的半径之和，从而得到L1=L2。

2.解题过程：L1=L2。理由如下：设n个小圆半径依次为r1，r2，…+rn，则大圆半径为r1+r2+…+rn，L2=πr1+πr2+…+πrn=π（r1+r2+…+rn）=L1。

3.考点分析：此题虽然改变了题目条件，但考点依然和原题保持了一致。

4.设计意图：改变小半圆半径的大小或位置（如图3、图4、图5），形成多元化的图形，增加学生对类似图形求周长的理解，考查学生对处理各种类似图形的处理能力，有利于培养学生的归纳能力和逻辑推理能力等数学素养。

【变式2】某公园计划砌一个形状如图6 所示的喷水池（图中长度单位：m），后来有人建议改为如图7 的形状，且外圆的半径不变，请你比较两种方案，确定哪一种方案砌各圆形水池的周边需要的材料多。（提示：比较两种方案中各圆形水池周长的和）

1.思路分析：先分别求出两种方案中各圆形水池周长的和，再比较大小。

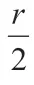
3.考点分析：本题来自人教版初中数学七年级上册75 页第9 题，本题的背景是整式的加减，所以它的考点主要就是含有字母的整式的合并同类项，同时也考查了学生对圆的周长的掌握，考查了总量等于各分量之和的数学思想，其思路方法与原题如出一辙。

4.设计意图：把原题半圆变成整圆，丰富图形的样式，考查了学生的识图能力，有利于培养学生的几何直观和逻辑推理等核心素养。

【变式3】如图8 所示，大正方形中有n个边长相等的小正方形，大正方形的周长为L1，内部图形的周长为L2（不包括与大正方形的重合部分），探索L1和L2的关系并证明你的结论。

1.思路分析：此题延续了原题的风格，都是大含小，而且大小图形都是相似图形，但是解题方法却大不同，对图形（题目）的理解至关重要。

3.考点分析：本题主要考查了学生对图形的理解识别能力，在结合代数式变形或整体代入思想的基础上沿用了原题解题的核心思路，是一道由原题改编而来的创新题型。

4.设计意图：把圆变成正方形，从求圆的弧长及周长迁移到求正方形的周长，同时也考查了几何图形的分析理解能力、等量代换等数学思想。

【变式4】某楼梯的侧面视图如图9 所示，其中AB=4 m，∠BAC=30°，∠C=90°，因为某种活动要求铺设红色地毯，则在AB段楼梯所铺地毯的长度应为多少米？

1.思路分析：由图可知，把每个小三角形的两条直角边分别平移到大直角三角形的边AC和BC上可知地毯的长度实际上等于大直角三角形的两条直角边之和。

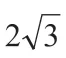
3.考点分析：本题考查了学生通过平移来理解总量等于各分量之和，也考查了对勾股定理的应用以及含有30°角的直角三角形的性质。

4.设计意图：把圆变成直角三角形，从求圆的弧长及周长迁移到求直角三角形的边长及周长，但依然考查了总量等于各分量之和的数学思想，也考查了几何图形平移的性质。

（四）感悟提升

通过变式教学，使学生灵活掌握圆的周长以及弧长公式，正方形的周长以及几何图形的平移性质、勾股定理的应用。从几何过渡到代数，从部分过渡到整体，学生的思维得到了发散，课堂教学效率得到了极大的提高，同时，在问题的有序变化中发现知识之间的内在联系，从而增强了举一反三、触类旁通的解题能力，很好地培养了学生的符号意识、几何直观及逻辑推理等数学素养。

（五）检测评价

1.如图10，大圆中有n个小圆，大圆的周长为L1，n个小圆的周长和为L2，探索L1和L2的关系并证明你的结论。

2.如图11，这是一个花台的平面图，正方形的边长为20 米，小圆的半径均为5 米，求这个花台的周长。

3.如图12，⊙A，⊙B，⊙C两两不相交，且半径都是0.5 cm。求图中三个扇形（阴影部分）的面积之和（可拓展到任意多边形）。

二、小结

本文以教材一道圆习题的变式教学探究为例，说明了几何题变式教学的“原题导入—原题探析—变式拓展—感悟提升—检测评价”五步课堂教学模式，为广大一线数学教师提供了参考模式。