星与星的联图点可区别I-全染色和点可区别VI-全染色

2020-08-03康慧君陈祥恩

广州大学学报（自然科学版） 2020年1期

康慧君，陈祥恩

(西北师范大学数学与统计学院，甘肃兰州 730070)

1 准备工作

图的点可区别正常边染色的研究见文献[1-7]，图的点可区别一般边染色的研究见文献[8-9]，图的点可区别正常全染色的研究见文献[10-13]，图的点可区别I-全染色和点可区别VI-全染色的研究见文献[14-19].本文讨论Sm与Sn的联图(3≤m≤n≤n+2)的点可区别I-和VI-全染色.

图G的一个使用了k种颜色的一般全染色(k-一般全染色)是指一个映射f：V∨E→{1,2…,k}.

图G的I-全染色，就是指对于这个图G的一个一般全染色f，∀u,v∈V,有f(u)≠f(v),∀e1,e2∈E,一旦e1与e2相邻，就有f(e1)≠f(e2).

图G的VI-全染色，就是指对于图G的一个一般全染色f，∀e1,e2∈E，一旦e1与e2相邻，就有f(e1)≠f(e2).

设f为图G的k-点可区别I-全染色，若∀u,v∈V(G),u≠v,有C(u)≠C(v)，称f为图G的k-点可区别I-全染色，记为k-VDITC，称为图G的点可区别I-全色数，记为即{k|G有k-VDVITC}.

同理，设f为G的k-点可区别VI-全染色，若∀u,v∈V(G),u≠v,C(u)≠C(v)，称f为图G的k-点可区别VI-全染色，记为k-VDVITC，称为图G的点可区别VI-全色数，记为即{k|G有k-VDVITC}.

设G(V1,E1)与H(V2,E2)，且V1∩V2=∅，E1∩E2=∅,称图G∨H为G与H的联，如果V(G∨H)=V1∪V2,E(G∨H)=E1∪E2∪{uv|u∈V1,v∈V2}.

对于一个简单图G，用ni表示度是i的顶点的个数，δ≤i≤Δ，假设

δ≤i≤i+s≤Δ,s≥0}.

猜想1[14](VDITC猜想)或ξ(G)+1.

猜想2[14](VDVITC猜想)或ξ(G)+1.

引理1[14]对于任意图G，如果存在两个Δ(最大度)顶点，则

引理2[14]

引理3[14]若图G只有一个最大度顶点，且则

引理4[14]如果存在正整数r，δ≤r≤Δ，且G没有度为r的顶点，则

ni+s,δ≤i≤i+s≤r-1,s≥0;或

r+1≤i≤i+s≤Δ,s≥0}.

命题1ξ(G)≤

假设p∈Z，而q为正整数，用(p)q表示{1,2，…，q}中的模q同余于p的那个数，即(p)q∈{1,2，…，q}且(p)q≡p(modq).

关于星与星的联图，有如下定义：

V(Sm∨Sn)={u1,…,um+1,v1,…,vn+1}，E(Sm∨Sn)=

{u1u2,u1u3,…,u1um,u1um+1,v1v2,v1v3，

v1v4,…,v1vn+1}∪{uivj|i=1,2,…,m+1;

j=1,2,…,n+1}.

d(ui)=n+2,i=2,3,…,m+1，度为n+2的点有m个；

d(u1)=m+n+1，d(v1)=m+n+1，度为m+n+1的点有2个；

d(vj)=m+2,j=2,3,…,n+1，度为m+2的点有n个.

2 主要结果

定理1 设Sm∨Sn是星Sm和星Sn的联,3≤m≤n≤n+2,且n=m,n=m+1，则

证明因为Δ(Sm∨Sn)=m+n+1,nΔ≥2由引理1可知，

则需要给出Sm∨Sn的一个(m+n+2)的点可区别I-全染色f.

分如下两种情况考虑：

情况1m=n.

第一步：给连接ui与vj的边进行染色，令

f(uivj)=(i+j-1)n+2，f(uivj)∈{1,2,…，

n+2}，1≤i≤m+1,1≤j≤n+1.

第二步：给两个星的边进行染色，令

f(uiuj)=αj-1,i=1,j=2,3,…,m+1，f(vivj)=αj-1,i=1,j=2,3,…,n+1，其中,α1,α2，…,αm是字母颜色.

第三步：给点染色，令

f(ui)=α1,i=2,3,…,m+1，f(u1)=α2,f(vj)=α3,j=2,3,…,n+1,f(v1)=α4.

对Sm和Sn的点进行染色时不要用{1，2，…，n+2}中的颜色，只用字母颜色染就够了，且Sm中用两种字母颜色，ui,i=2,3,…,m+1只用一种颜色染，对Sn用同样的办法进行染色.

上述染色是I-全染色，并且在此染色下有:

C(u1)={1,2,…,n,n+1}；

C(u2)={2,3,…,n,n+1,n+2}；

C(u3)={3,…,n,n+1,n+2,1}；

C(u4)={4,…,n,n+1,n+2,1,2}；

⋮

C(um+1)={m+1,m+2,…,n,n+1,n+2,1,…,m-1}.

C(v1)={1,2,…,m,m+1}；

C(v2)={2,…,m,m+1,m+2}；

⋮

C(vn+1)={n+1,n+2,1,…,n-3}.

容易验证f是I-全染色，接下来证明f是点可区别的.

事实1：C(u1),C(u2),…C(um+1)是互不相同的色集合.

事实2：C(v1),C(v2),…C(vn+1)是互不相同的色集合.

证明每个C(ui)都包含除了i-1的所有数字颜色，i=1,2,…,m+1，因为起始点i是不同的，因此,C(u1),C(u2),…C(um+1)是互不相同的.

因为m=n，所以字母颜色α1,α2，…,αm刚好可以给两边星的边染色，关联边用数字颜色，Sm和Sn的顶点至少用四种颜色染色，由此可见,m+n+2个点的色集合彼此不相同，从而得知上述I-全染色是点可区别的.

当m=n=3时，Sm∨Sn有2个7度(最大度)的点，由引理1知，只需给出(S3∨S3)的一个8点可区别I-全染色f，令

f(uivj)=i+j-1,i=1,2,3,4,j=1,2,3,4;

f(u1vj)=j,j=1,2,3,4；f(u2vj)=j+1,j=1,2,3,4；

f(u3vj)=j+2,j=1,2,3,4；f(u4vj)=j+3,j=1,2,3,4；

f(u1)=1,f(ui)=2,i=2,3,4；f(v1)=3,f(vj)=4,j=2,3,4；

f(u1u2)=6;f(u1u3)=7;f(u1u4)=8；f(v1v2)=6;f(v1v3)=7;f(v1v4)=8.

上述染色是I-全染色，并且在此染色下有

情况2n=m+1.

第一步：给连接ui与vj的边进行染色，令

f(uivj)=(i+j-1)n+2,f(uivj)∈{1,2,…,n+2},1≤i≤m+1,1≤j≤n+1.

第二步：给两个星的边进行染色，令

f(u1ui)=αi-1,i∈{2,3,…,m+1}；f(v1vj)=αj-1,j∈{2,3,…,m+1}；

当j=n+1时，f(v1vn+1)=n-1.

第三步：给两边的点染色，令

f(ui)=α1,i=2,3,…,m+1，f(u1)=α2,

f(vj)=α3,j=2,3,…,n+1,f(v1)=α4；

只用字母颜色染色，且只需四种字母颜色染色就够了.

上述染色是I-全染色，并且在此染色下有:

C(u1)={1,2,…,n,n+1}，缺数字颜色n+2;

C(u2)={2,3,…,n,n+1,n+2}，缺数字颜色1；

C(u3)={3,…,n,n+1,n+2,1}，缺数字颜色2；

⋮

C(um+1)={m+1,m+2,…,n,n+1,n+2,1,…,m-1}，缺数字颜色m.

C(v1)={1,2,…,m,m+1}，缺颜色m+2，m+3，即n+1，n+2；

C(v2)={2,…,m,m+1,m+2}，缺颜色1，m+3;

⋮

C(vn+1)={n+1,n+2,1,…,n-3}，缺颜色n，n-1.

对于顶点u1和v1进行染色，共包含2m+2种颜色，其中C(u1)≠C(v1).

对于m+n-1个顶点u2,u3,…,um+1和v2,v3…,vn+1,使得|C(ui)|=m+4,i=2,3,…,m+1,|C(vj)|=m+4,j=2,3,…,n,根据事实1和事实2，C(u1),C(u2),…C(um+1)和C(v1),C(v2),…C(vn)是互不相同的，可区别的.

对于顶点vn+1，色集合包含m+2种颜色，C(v1),C(vn+1)包含的颜色不同，因此，色集合C(v1)≠C(vn+1)，并且，C(u1)包含颜色1，但C(vn+1)不包含颜色1，所以C(u1)≠C(vn+1)，由此可见，C(u1)≠C(vn+1)≠C(v1).

由此可见,m+n+2个点的色集合彼此互不相同，从而得知上述I-全染色是点可区别的.

当n=4,m=3时，S3∨S4有2个8度(最大度)的点，由引理1，则

假如S3∨S4存在9-点可区别全染色，使用的颜色为1,2，…，9.只需给出一个9-点可区别I-全染色即可，令

f(uivj)=i+j-1,i=1,2,3,4,j=1,2,3,4，5;

f(u1)=1,f(ui)=2,i=2,3,4；f(v1)=3,f(vj)=4,j=2,3,4,5；f(u1u2)=7;f(u1u3)=8;f(u1u4)=9；f(v1v2)=6;f(v1v3)=7;f(v1v4)=8;f(v1v5)=9.

由此可见,上述染色是I-全染色，并且9个点的色集合彼此互不相同，从而是点可区别的.

定理2 设Sm∨Sn是星Sm与星Sn的联，3≤m≤n≤n+2，且n=m+2，则

m+n+2≤

证明因为ΔSm∨Sn=m+n+1,m+n+2≤只需给出Sm∨Sn的一个(m+n+3)-点可区别I-全染色f.

第一步：给连接ui与vj的边进行染色，令

f(uivj)=(i+j-1)n+2,f(uivj)∈{1,2,…,n+2},1≤i≤m+1,1≤j≤n+1.

第二步：给两个星的边进行染色，令

f(u1ui)=αi-1,i∈{2,3,…,m+1}；

f(v1vj)=αj-1,j∈{2,3,…,m+1}，

因为n=m+2,所以Sn中的边有两条不能用字母颜色进行染色，必须用数字颜色来染色.

第三步：给点染色，令

f(ui)=α1,i=2,3,…,m+1，f(u1)=α2,

f(vj)=α3,j=2,3,…,n+1,f(v1)=α4.

上述染色是I-全染色，并且在此染色下有：

C(u1)={1,2,…,n,n+1}，缺数字颜色n+2;

C(u2)={2,3,…,n,n+1,n+2}，缺数字颜色1；

C(u3)={3,…,n,n+1,n+2,1}，缺数字颜色2；

⋮

C(um+1)={m+1,m+2,…,n,n+1,n+2,1,…,m-1}，缺数字颜色m；

C(v1)={1,2,…,m,m+1}，缺数字颜色m+2，m+3，m+4即n，n+1，n+2；

C(v2)={2,…,m,m+1,m+2}，缺数字颜色1，m+3，m+4即1，n+1，n+2；

⋮

C(vn)={n,n+1,n+2,1,2,…,n-4}，缺数字颜色n-1，n-2，n-3；

C(vn+1)={n+1,n+2,1,…,n-3}，缺数字颜色n，n-1，n-2；

用上述染色给n=m+2的星进行染色，则发现Sn中的两条边v1vn和v1vn+1，v1vn+1可以用数字颜色n进行正常染色，v1vn无法正常染色.

当m=3，n=5时，

假如S3∨S5存在10-点可区别I-全染色，用上述方法给S3∨S5染色，令

f(uivj)=(i+j-1)n+2,f(uivj)∈{1,2,…,7},1≤i≤4,1≤j≤6；

由于

f(v1ui)={1,2,3,4},i=1,2,3,4；f(v5ui)={5,6,7,1},i=1,2,3,4；

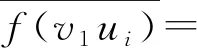
可以看出，f(v1ui)和f(v5ui)的补集的色集合没有相同的颜色数，从而S5当中的边v1v5不能正常染色，而边v1v6可以用相同的颜色数5正常染色.

所以,对于n=m+2的情形，不存在10-点可区别I-全染色.

f(uivj)=(i+j-1)n+2,f(uivj)∈{1,2,…,7},1≤i≤4,1≤j≤6.

继续取模长为n+2，则字母颜色为α1、α2、α3、α4，点ui与vj染其关联边的颜色，其中关联边用数字颜色染色，顶点用四种数字颜色染色，并且相邻点着不同色，S3内部的联边u1u2、u1u3、u1u4分别用α1、α2、α3进行染色，S5内部的联边v1v2、v1v3、v1v4、v1v5、v1v6分别用α1、α2、α3、α4、α5进行染色.

最终得到的上述全染色是I-全染色，并且在此染色下有：

C(u1)={1,2,3,4,5,6,α1,α2,α3}；C(u2)={2,3,4,5,6,7,α1}；

C(u3)={3,4,5,6,7,1,α2}；C(u4)={4,5,6,7,1,2,α3}；

C(v1)={1,2,3,4,α1,α2,α3}；C(v2)={2,3,4,5,α1}；

C(v3)={3,4,5,6,α2}；C(v4)={4,5,6,7,α3}；

C(v5)={5,6,7,1,α4}；C(v6)={6,7,1,2,5}.

由此可见，10个点的色集合彼此不相同，从而得知上述I-全染色是点可区别的.

当n=m+2时，现在只需证明Sm∨Sn有一个(m+n+3)-VDITCf.令

f(uivj)=(i+j-1)n+2,f(uivj)∈{1,2,…,n+2},1≤i≤m+1,1≤j≤n+1；

f(u1ui)=αi-1，i=2,3,…,m+1，f(v1vj)=αj-1,j≠1,n+1；

f(v1vn+1)=n,j=n+1.

最终得到的上述全染色是I-全染色，并且在此染色下有: