基于非接触式电导信号的土壤速效钾含量检测方法

李传文,魏圆圆,陈翔宇*,张俊卿,郭红燕,王儒敬*

(1.中国科学院 合肥智能机械研究所，安徽 合肥 230031；2.中国科学技术大学，安徽 合肥 230026)

变量施肥需精准感知农田土壤养分分布。由于速效钾起着供给作物钾的重要作用，且是植物生长和发育必需的营养物质，故而是衡量土壤向农作物供应钾能力的重要指标[1-3]，但是土壤中钾含量过高会导致资源浪费、土壤环境污染、水污染以及土壤养分分布不平衡等问题。目前，土壤中速效钾含量的传统测定方法主要有火焰光度计法和火焰原子吸收法等，虽然具有较高精度，但过程繁琐，需耗费大量的人力、物力和财力，且往往具有滞后性[4]。因此，建立快速、准确地检测土壤中速效钾含量的分析方法对农业发展具有重要意义。

随着科学技术的进步，国内外学者将许多新方法应用于土壤速效钾含量的测定。可见/短波近红外光谱法因其分析速度快、成本低以及再现性好等优点而被应用于土壤速效钾的检测[5-8]，但因钾在近红外区无特定吸收波段，其含量的光谱预测可能归因于钾与光谱活跃成分局部存在相关关系，且不同类型土壤中钾的含量及组成差异较大，因而预测效果不稳定[9]。高光谱遥感技术不仅具有近红外光谱的优点，还可大范围动态检测，因而得到广泛研究[4,9-11]，但其依然存在红外光谱检测的缺点。X射线荧光法(pXRF)已被成功应用于表征土壤元素组成[12-13]，但在钾离子的检测精度上有待提高。非接触式电导检测(Capacitively coupled contactless conductivity detection,C4D)因灵敏度高、成本低、性能稳定等优点被应用于复杂样品检测[14-15]。张俊卿等[16]采用自制的高效毛细管电泳/非接触式电导检测装置对6种土壤样品的钾离子含量进行了测试，测定结果与标准值的趋势一致，且二者存在相关关系，说明非接触式电导检测装置能完成土壤钾离子的初步检测，但该方法是基于标准加入法，且采用非接触式电导信号特征峰峰强定量分析时未考虑峰谱重叠问题。

土壤样品测试得到的非接触电导信号峰谱中，因不同离子出峰位置接近而导致峰重叠，影响了峰谱模型的建立。为此，本文将Levenberg-Marquardt(L-M)的高斯分峰拟合算法与偏最小二乘法(PLS)相结合，建立了土壤中速效钾含量的预测模型。方法首先进行初步识别峰谱，再引入基于L-M的高斯分峰拟合算法实现单峰和重叠峰的拟合计算，得到高斯峰和相应的特征参数(包括峰位、峰高、半峰宽和峰面积)，最后采用拟合得到的高斯峰及相应的特征参数表征原始非接触式电导信号离子峰谱信息，结合偏最小二乘法，确定特征参数与土壤速效钾含量的关系，建立模型，并对模型的精度进行评定。研究结果表明，结合基于L-M的高斯分峰拟合算法的非接触式电导检测方法有望应用于土壤中钾含量的快速分析。

1 理论与方法

对于非接触式电导信号数据的峰谱解析包括峰检测、峰筛选和峰拟合。首先，采用导数法与高斯曲线拟合法相结合进行峰谱识别；然后对检测到的峰按条件去除伪峰；最后使用L-M算法对拟合的高斯峰进行参数优化，得到离子峰特征参数，并由其计算峰面积。使用经参数优化后的高斯峰特征参数构建离子峰信息矩阵，结合偏最小二乘法构建土壤中速效钾含量预测模型，并建立评价指标。

1.1 峰谱识别

土壤的非接触式电导信号中包含多个峰谱，分别表征不同的离子，因此需进行峰谱识别。导数法中，一阶导数反映了峰谱曲线在一点的附近变化率，而二阶导数则显示了峰谱曲线的凹凸性，将两者结合可快速识别峰谱，但导数法易受噪声影响。为提高准确性，在导数法确定峰位后，以峰位为中心，按峰顶部测量点数数值取点，进行高斯拟合，以确定参数，得到预设边界。

非接触式电导检测实际采样过程中得到的是离散数据，但因2次采样的时间间隔非常短(0.000 4 s)，所以可使用相邻两数据点的差值作为一阶导数值。同理，可求得非接触式电导信号的二阶导数。非接触式电导信号谱图中的峰类型及其一阶导数和二阶导数曲线如图1所示。

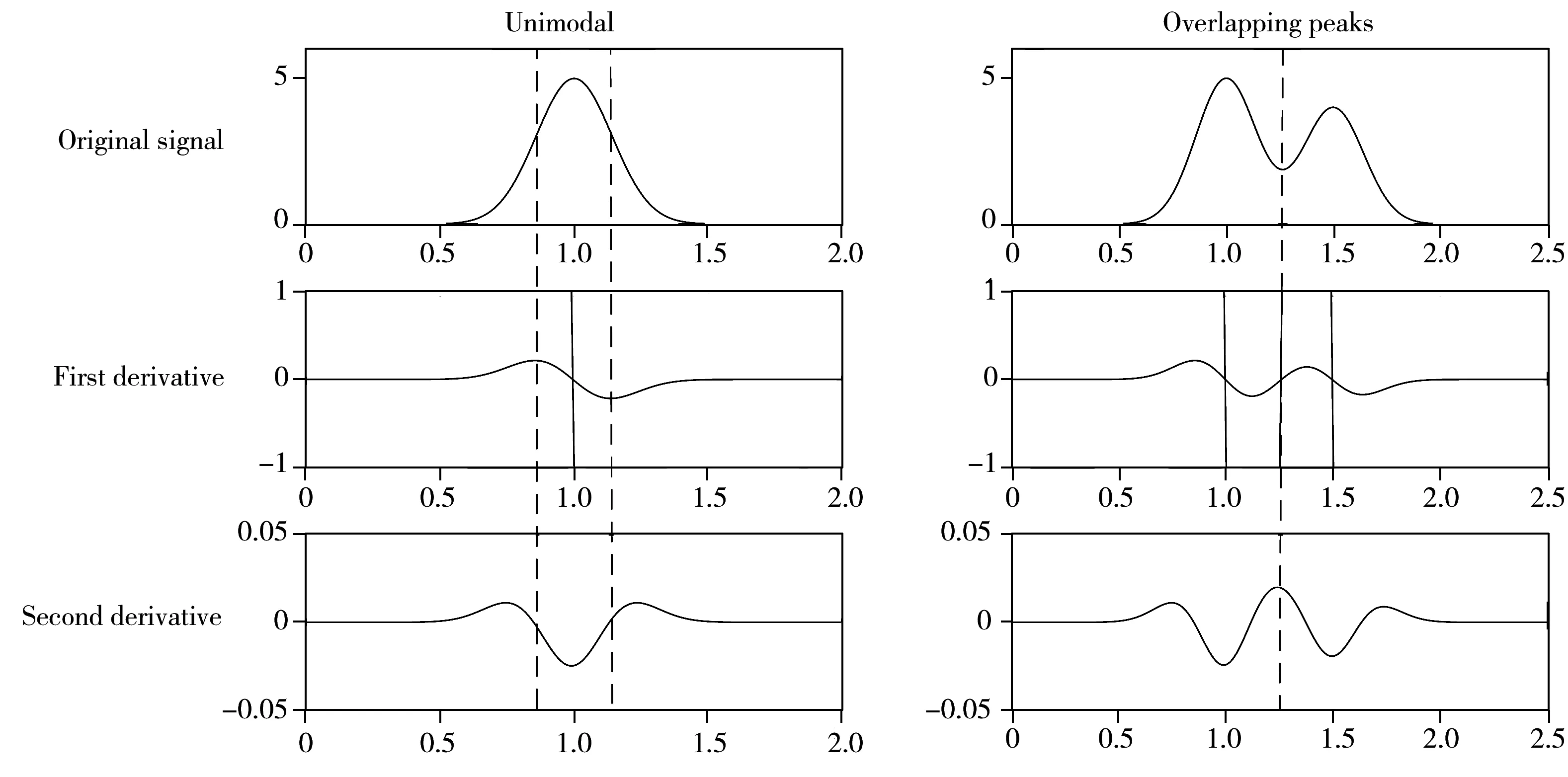
图1 非接触式电导检测信号峰及其一阶、二阶导数Fig.1 Peak original signal,first and second derivative of C4D

基于导数-曲线拟合法实现非接触式电导信号峰谱识别的过程如下：设原始电导信号为f，其一阶导数为d，二阶导数为s。δ为一阶导数f的标准差，对一阶导数取sign(d(t))值记为D。由于非接触式电导信号中存在噪声和基线漂移，为减少干扰，引入零斜率区[-T，T]，即在该区间内被认为是基线处斜率。通常认为随机噪声与基线漂移的斜率变化服从正态分布且具有零均值特性。一般情况下，当n>100时，T=3δ2可以保证97.3%的基线斜率落在该区间内[17]。

峰谱识别及其特征点判别如下：

①峰顶点判别：当sign(d(t))>sign(d(t+1))，且f(t)>f(t-1)，f(t)>f(t+1)，d(t)-d(t+1)>3δ2，f(t)>3δ2时，判定为峰顶点。

②以峰顶点处为中心，按给定峰顶部测量点数值取点，并进行高斯拟合，初步确定峰位、峰值和半峰宽，并得到预设边界。

③峰起始点判别：以峰顶点为中心，在预设边界范围内向负方向移动，当f(t)>f(t-1)，d(t)>3δ2，d(t-1)<3δ2，且s(t)>3δ2，s(t-1)<3δ2时，判定为峰起点。

④峰谷点判别：以峰顶点为中心，在预设边界范围内向正方向移动，当sign(d(t))3δ2时，判定为峰谷点。

⑤峰终止点判别：以峰顶点为中心，在预设边界范围内向正方向移动，当f(t)>f(t+1)，d(t)>3δ2，d(t+1)<3δ2，且s(t)>3δ2，s(t+1)<3δ2时，判定为峰终止点。

经上述方法处理后，可实现特征点识别，从而达到初步的峰谱识别。

1.2 峰值过滤

初步峰检测后获得的峰数量一般大于实际峰谱数量。因此，在估计好仪器的噪声水平后，进行峰消除程序可验证峰是真实峰还是简单伪像。满足以下两个条件才能视为有效峰：

①计算原始非接触式电导信号的峰谱与拟合高斯峰信号峰谱的残差(Error)，当残差标准差超过2(该值表示可以在非接触式电导信号谱图中准确定量记录点数的经验值)时，峰被删除，Error的计算公式如下：

Error=原始信号数据点-拟合信号数据点

(1)

②计算峰区域内一阶导数绝对值大于阈值T的次数n1和二阶导数越过零线的次数n2，当n1<5或n2>8时，可认为该峰为嘈杂峰，记为伪峰，并删除该峰。

1.3 基于L-M的高斯拟合

经过初步谱峰识别和峰值过滤后，获得了非接触式电导信号中峰谱的数量N以及每个峰对应高斯函数表达式的峰高(hi)、峰位(ti)和半峰宽(wi)。再采用L-M算法优化，从而获得更接近原始数据峰谱的高斯峰参数。

L-M算法属于二阶算法，是Gauss-Newton(GN)算法的改进,通过引入参数μk，将GN算法与最速梯度法结合。当μk较小时，所拟合数据远离收敛点，L-M算法则类似于最速梯度法，具有较强适应性；当μk较大时，所拟合数据接近收敛点，L-M算法则近似于GN法，具有快速收敛性。因此，L-M算法被广泛用于数据拟合优化中，其优化目标可表示如下：

(2)

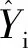
L-M算法的迭代公式如下：

(3)

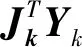
L-M算法的具体实现过程如下：①给定允许误差ε和最大迭代次数kmax，初始化权值向量x，k=0；②计算拟合函数及J、H矩阵，然后得到迭代步长hlm；③计算更新后权值向量与旧权值向量间的误差，若小于ε则退出程序，否则进入步骤④；④计算误差向量下降量ΔEk=E(xk)-E(xk-1)，根据ΔEk值更新μk；⑤判断当前迭代次数是否大于最大迭代次数kmax，若大于kmax则退出程序，否则返回步骤②。

1.4 模型构建及评价

偏最小二乘回归分析模型是在化学计量学中广泛应用的建模方法。相比于传统多元线性回归，偏最小二乘法不但能同时分解非接触式电导信号信息矩阵和土壤离子含量矩阵，而且能很好地消除噪声干扰，因而具有很强的预测能力。

通过实测值与预测值计算模型的决定系数(R2)、均方根误差(RMSE)和相对分析误差(RPD)来评定模型的预测效果。R2直接决定了模型预测值与实测值之间的相关程度，其值越大，表明建模精度越高；RMSE反应了两者之间的偏离程度；RPD反映了模型的预测能力。当RPD≥2.5时，表明模型具有极好的回归能力，2.0≤RPD<2.5表示模型具有很好的定量回归能力；1.8≤RPD<2.0表示模型具有较好的定量回归能力；1.4≤RPD<1.8表示模型具有定量回归能力；1.0≤RPD<1.4表示模型具有区别高值和低值的能力；当RPD<1.0时，表示模型不具备回归能力。

2 实验部分

2.1 仪器与试剂

CE-IIM-651A型毛细管电泳池及高压电源、CE-IIM-C4D-652型非接触式电导检测器(合肥智能机械研究所)；熔融石英毛细管(上海连舰光电科技有限公司)；AP1200火焰光度计(上海傲谱分析仪器有限公司)；AUY220分析天平(岛津企业管理(中国)有限公司)；DKZ-2往复式振荡机(上海一恒科学仪器有限公司)；JP-020S超声波清洗器(深圳市洁盟清洗设备有限公司)。

标准物质：三羟甲基氨基甲烷(Tris)、乙二胺四乙酸(EDTA，非钠盐)、聚乙烯吡咯烷酮(PVP，平均分子量M=30 000)、硝酸钾、氢氧化钠(分析纯，上海阿拉丁生化科技股份有限公司)；冰醋酸、氯化铵、硝酸钾(分析纯，国药集团药业股份有限公司)；实验用超纯水由Milli-Q超纯水系统制备。

pTAE Buffer母液：分别精密称取3.03 g Tris和0.18 g EDTA于50 mL洁净塑料瓶中，加入约40 mL水，摇匀，使其充分溶解，再加入0.30 mL冰乙酸，充分溶解，用水定容至刻度；毛细管电泳运行液：精密称取0.60 g PVP于洁净塑料烧杯中，用适量水溶解后，转移至100 mL容量瓶中，再加入2 mL pTAE Buffer母液，然后用水定容至刻度；200 mg/L钾离子(K+)标准溶液使用硝酸钾配制。

2.2 样品前处理

实验选用河南潮土，并使用土样在采集中划分的编号进行命名，风干后过1 mm孔径筛，精密称取3.0 g(精确至0.01 g)土样于200 mL塑料瓶(或100 mL三角瓶)中，加入30 mL水，旋紧瓶塞(或封口膜封口)，于20～25 ℃下以150～180 r/min振荡30 min，用定量滤纸过滤。滤液经一次性注射器推过针头式过滤器(0.45 μm/25 mm，生工生物工程(上海)股份有限公司)进行再次过滤，取滤液放入洁净的2 mL塑料样品管内，待测。

2.3 仪器条件

环境温度25 ℃，采用CE-IIM-C4D-652型非接触式电导检测器检测，由N2000+(智达信息工程有限公司)软件采集数据。熔融石英毛细管(35 cm×50 μm i.d.，Leff = 39 cm)。电进样模式：设置高压电源为+10 kV，时间为5 s。样品测试模式：设置分离电压为+13.5 kV；样品体积为1 mL，钾标准溶液浓度cK+为200 mg/L，向样品中加入钾标准溶液的体积为0.05 mL，测试时间为6 min。

2.4 实验方法

2.4.1 火焰光度计分析将经前处理后的样品滤液直接在火焰光度计上测定，同时做空白试验。

标准曲线的绘制：分别精密移取0.00、0.625、1.25、2.50、3.75、5.00、6.25 mL 200 mg/L钾标准溶液于50 mL容量瓶中，用水定容，配成0、2.5、5.0、10、15、20、25 μg/mL的系列钾标准溶液，以钾浓度为0的溶液调节仪器零点，再用火焰光度计测定，绘制钾离子的标准曲线。

2.4.2 非接触式电导检测仪分析清洗：用水清洗毛细管两端及铂金电极等；将检测池和储液瓶在超声波清洗机中用水超声清洗2 min，再用运行液清洗储液瓶和检测池3次，并向其中各加入适量的电泳运行液。毛细管内部采用特制注射器清洗，第一次使用的毛细管依次用0.1 mol/L氢氧化钠溶液、水与电泳运行液各清洗5 min。冲洗完毕后，将毛细管的两端完全浸没在检测池和储液瓶中的电泳运行液中，且尽量保持两端在同一水平上。

背景采集：启动高压电源，使用数据采集软件记录，可观察到屏幕上显示出基线，6 min后停止采集并关闭高压电源。若基线稳定，准备进样；若基线不稳定则需排除原因，再进行基线测试；若基线中出现杂质峰，则需再次清洗后进行基线测试。

土壤样品溶液电进样：取下储液瓶，将样品架上待测样品溶液移入毛细管进样口位置。使用高压电源，启动仪器电进样程序，待电压值重新归零后，将样品架移出，重新装上储液瓶，并保证电极与毛细管末端浸入运行液中。

样品测试：启动分离电压，并开始记录采集的数据，可观察到屏幕上显示出电泳谱线，待电泳峰出现后，关闭分离电压。该电泳谱图会自动保存在设置路径的文件夹内。

3 结果与讨论

3.1 仿真非接触式电导信号的峰谱检测

非接触式电导信号谱图与色谱图表现形式相同，即电导信号随着离子的迁移，从基线位置上升到峰值，随后又逐渐回落到基线。为评估本方法的检测性能，基于非接触式电导检测的基本原理，使用高斯函数模拟了信号峰谱图。非接触式电导信号峰谱的曲线方程如下：

(4)

式中，base为基线漂移，理想情况下为0；N为峰个数；hi为各峰的峰高；tRi为各峰的峰位；ωi为半峰宽；峰谱图中的峰序号用i表示。

考虑到实际获取的检测信号中混有噪声，因此在模拟得到的峰谱图中加入高斯白噪声。最终得到含噪非接触式电导信号函数模型：

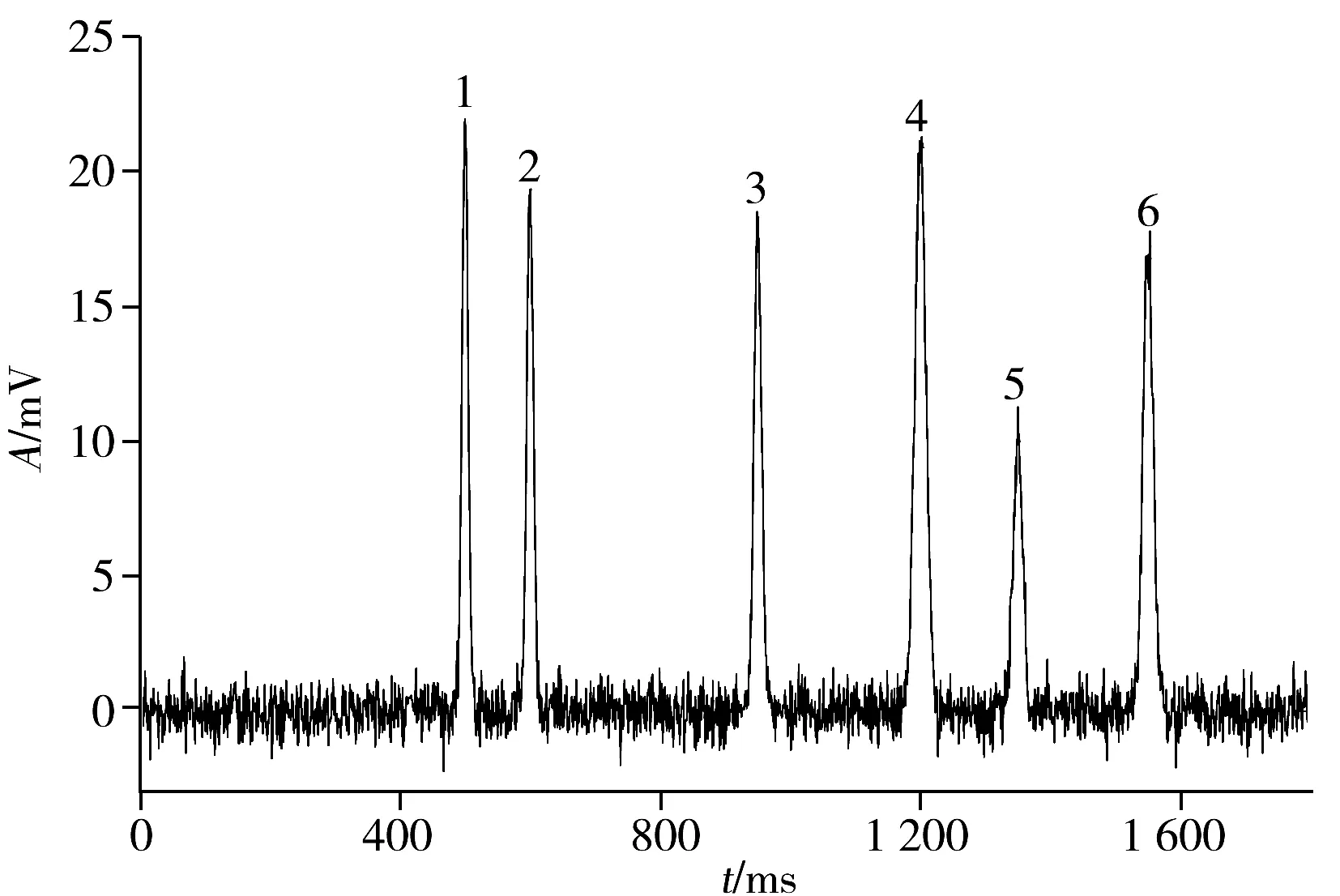
图2 非接触式电导信号单峰仿真谱图Fig.2 Single-peak simulation spectrum of C4D signal the peak number 1-6 were the same as those in table 1

Y(t)=y(t)+noise(t)

(5)

式中：y(t)为信号峰曲线，noise(t)为高斯白噪声。

3.1.1 单峰检测根据公式(5)建立含噪非接触式电导信号单峰谱图，并按信噪比(SNR)15、20、30、40 dB依次分为4组，每组仿真1 000次。设置评价参数：峰位(Position)、峰高(Height)、半峰宽(Full width at half maxima，FWHM)、峰面积(Area)与设定值之差的均值为μt、μh、μω、μs及标准差为σt、σh、σω、σs。图2为一包含6个高斯峰，信噪比为15 dB的非接触式电导信号单峰仿真谱图，其峰谱曲线设定参数值如表1所示。4组信噪比下的评价参数值如表2所示。

表1 非接触式电导信号的单峰谱曲线参数Table 1 Peak-spectrum curve parameters of C4D signal

表2 不同信噪比下的仿真评价参数Table 2 Evaluation parameters under different SNR

结合图2与表2可见，在信噪比为15 dB时为较嘈杂的信号谱图，但峰位和半峰宽识别误差仍分别达到0.001 ms和0.01 ms数量级。从表2中的仿真结果可见，信噪比由15 dB增加至40 dB过程中，各评价参数值均在变小，即检测值精度不断提升。综上，可得出本方法检测单峰峰谱精度较高，且在峰位处的识别误差达到0.000 1 ms量级。

3.1.2 重叠峰检测为验证本算法对非接触式电导信号重叠峰谱图分析的能力，从色谱领域引入分离度(R)来表示峰谱的重叠程度，分离度越小，表明峰谱重叠度越高，分离度计算公式如下：

(6)

式中，R为重叠峰的分离度，t1和t2分别为两个峰谱的峰位，ω1和ω2分别为两个峰谱在10%峰高处的峰宽。

重叠峰常由一个弱峰和一个强峰组成，将具有不同特征参数的理想仿真信号叠加，得到仿真重叠峰谱信号。保持弱峰各参数不变，通过改变强峰的峰位，可得到不同分离度下的重叠峰谱图(图3)。

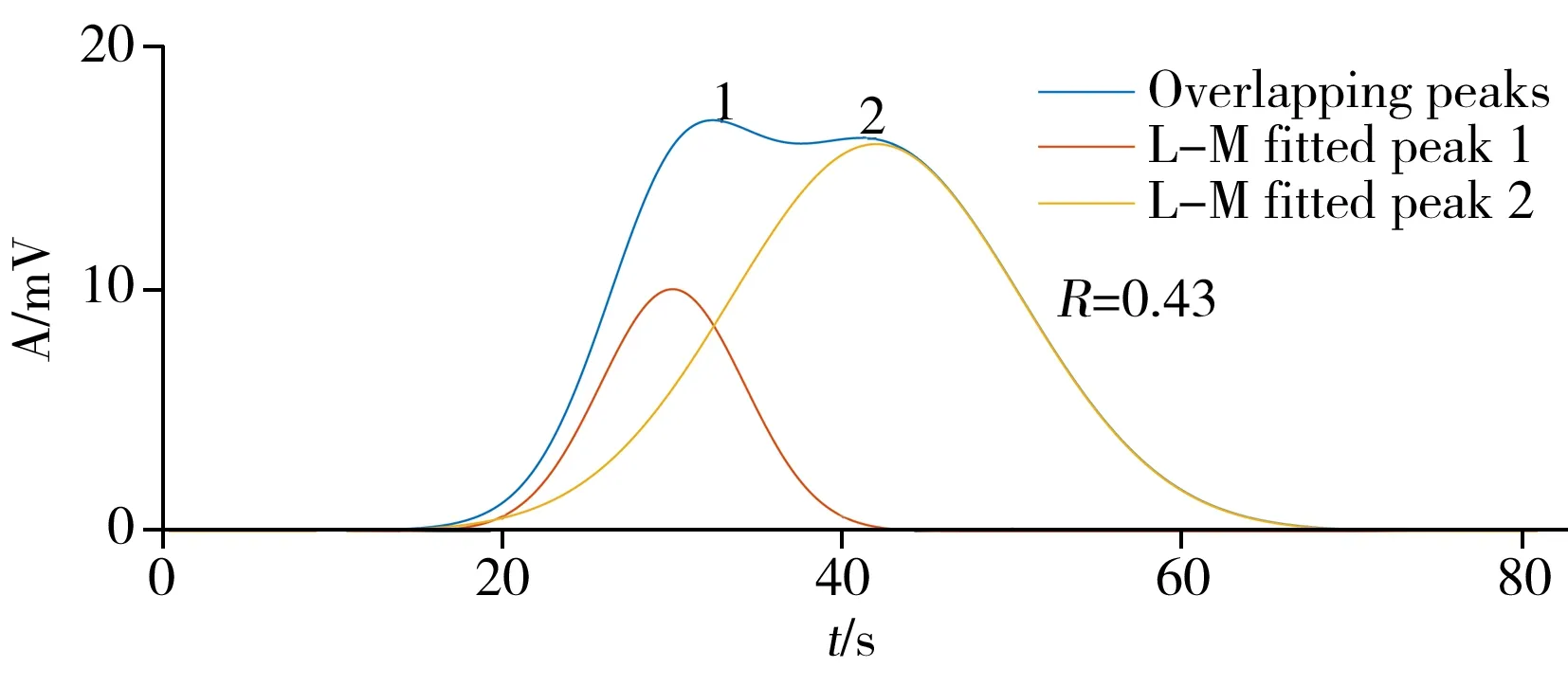
图3 不同分离度下的重叠峰谱图Fig.3 Overlapping peaks spectrum at different resolutions

使用本算法对仿真重叠峰谱数据进行验证，经50次迭代后，可获得图3的拟合峰谱，表3为仿真峰谱的设定参数值、导数法结合高斯拟合法寻峰获得的初始参数值以及经L-M算法拟合后的拟合参数值。

表3 不同分离度下的初始参数、设定参数及L-M参数Table 3 Initial parameters, initial fitted and L-M fitted results at different resolutions

结合图3与表3可见，当峰谱的分离度较小，即两峰谱重叠度较高时，使用导数法结合高斯拟合法得到的单峰峰谱初始参数与真实的设定参数之间可能存在较大误差，经过L-M算法对初始参数优化后，可获得与设定参数十分接近的拟合参数；随着分离度的增加，两峰谱逐渐分离，初始参数与设定参数之间的误差逐渐缩小，经过L-M算法对初始参数优化后，拟合参数等于设定参数。由此可见，本算法理论上可以获得较好的结果。

3.2 非触式电导信号测定土壤速效钾

基于毛细管电泳实验的非接触式电导检测获取的离子信号峰谱参数可以表征离子含量，但由于真实谱图中峰谱参数的真实值未知，无法比较峰谱参数检测精度。因此采用标准加入法来验证本方法处理真实非接触式电导信号的有效性，并与火焰光度计法获取的土壤速效钾含量进行比较。

河南潮土样品经处理后，通过非接触式电导检测获取信号峰谱(图4A)。经本算法处理后，可识别出单峰和重叠峰，并按相应程序进行拟合。单峰初始拟合曲线和重叠峰初始拟合曲线经L-M算法参数优化后结果分别见图4B、C所示。经L-M算法参数优化后，单峰初始拟合曲线的均方根误差(RMSE)由2.305 0降至0.910 6，重叠峰初始拟合曲线的RMSE由0.503 8降至0.498 0。所有样本经L-M的高斯拟合前的RMSE均值为2.463 2；而经L-M高斯拟合后RMSE均值为1.119 1，降至原来的45%，表明该算法具有较好的拟合效果。

图4 河南潮土样品的非接触式电导信号及拟合曲线Fig.4 C4D signal in Henan fluvo-aquic soil sample and its fitting curves A.C4D signal spectrum,B.singlet fitting,C.overlapping peaks fitting

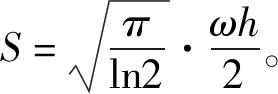
表4 速效钾经非接触式电导法与火焰光度计法的检测结果比较Table 4 Comparison of analysis results of available potassium by C4D and flame photometer method

3.3 土壤速效钾含量的回归模型

对土壤样本数据通过基于L-M的高斯拟合优化算法得到钾离子峰谱信息矩阵，并利用标准加入法计算得土壤中钾离子含量。钾离子峰谱信息矩阵为四维特征自变量组，对应的钾离子含量为一维因变量组，使用偏最小二乘法建立土壤速效钾含量的预测模型。从总体样本中抽取80%作为校正集，20%作为验证集。总体样本、校正集样本和验证集样本中土壤钾离子含量统计结果如表5所示。校正集与验证集所对应的均值分别为16.483 6 mg/kg和16.773 7 mg/kg，相对标准偏差(标准差与平均值比值)分别为50.50%和56.88%。而总体样本均值为16.543 5 mg/kg，相对标准偏差为51.93%。由此可见，总体样本的均值和变异系数均处于校正集与验证集之间。

表5 被测土壤样品中钾离子含量的测定结果Table 5 Test results of available potassium in soil samples

根据土壤实测钾离子含量及相应的高斯峰谱特征参数矩阵数据，构建PLS回归模型，主因子数为4，图5为验证集样本土壤速效钾含量预测值与实测值的散点图，回归结果如表6所示。由表6可见，使用高斯拟合获取的峰谱特征参数矩阵构建回归模型，其相对分析误差(RPD)均大于2，适合土壤钾离子含量建模，均有较好的回归能力，但回归模型的决定系数R2为0.812，表示建模精度欠佳。而使用基于L-M的高斯拟合获取峰谱特征参数矩阵构建回归模型，该模型的各项评价指标均得到提升，相对分析误差为2.639，具有很好的回归能力；回归模型的决定系数R2为0.856 4，具有较高的建模精度。

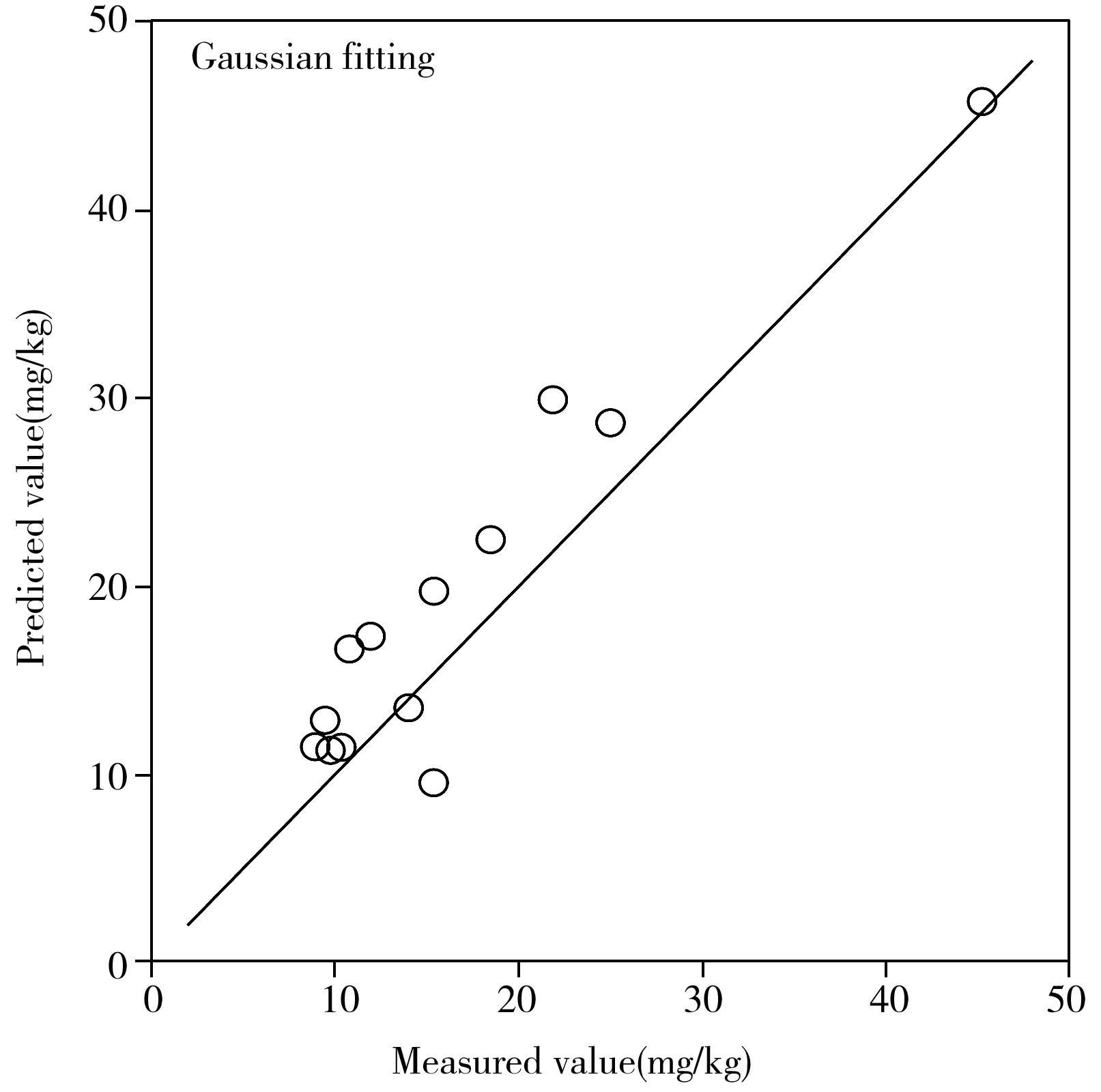
图5 验证集样本土壤速效钾含量实测值与预测值散点图Fig.5 Available potassium predicted and measured values for validation set

表6 土壤速效钾含量模型评价结果Table 6 Evaluation results of soil available potassium content model

4 结 论

本文通过高效毛细管电泳/非接触式电导检测仪采集河南潮土速效钾信息的非接触式电导信号，并使用导数法结合高斯曲线拟合法进行初步峰谱识别，经峰值过滤后，采用基于L-M的高斯拟合算法对实际峰谱进行单峰/重叠峰拟合计算，用拟合得到的高斯峰特征参数表征原始非接触式电导信号的离子峰谱信息，实现了数据简化。将基于L-M的高斯拟合得到的高斯特征参数与偏最小二乘法结合，建立了土壤中速效钾含量的预测模型。结果表明，应用高斯拟合对土壤钾离子的非接触式电导信号进行分析，可以预测土壤中钾离子含量，且与峰谱识别时直接进行高斯拟合相比，基于L-M的高斯拟合建立的预测回归模型具有更优的预测效果，适用于土壤中速效钾的快速检测分析。