基于FOA-LSSVM算法的扩散硅压阻式压力传感器温度补偿

尹家乐,卢文科,左 锋,张 珏

(东华大学信息科学与技术学院，上海 201600)

0 引言

随着科学技术的发展，各领域对于压力的测量精度要求越来越高。扩散硅压阻式压力传感器具有灵敏度高、精度高、可靠性能好、动态响应快等特点，广泛应用于航空、航天、石油化工、地震测量等领域[1-3]。

扩散硅压阻式压力传感器采用了半导体的扩散技术和压阻效应制作硅电阻条，并用四个硅电阻条连接成惠斯通电桥电路。由于半导体材料对温度的敏感性以及硅电阻条制造工艺的局限性，因此该传感器存在温度漂移现象，必须对其进行温度补偿[4-5]。当前，国内外的温度补偿技术分为硬件补偿和软件补偿两大类。硬件补偿的电路复杂、调试困难、且硬件电路本身会受温度影响，对温度漂移的抑制效果并不明显，不利于工程应用。软件补偿结合数学方法和计算机技术，其精度高、易于调试、应用广泛。因此软件补偿是温度补偿常用的方法。

软件补偿方法一般有反向传播(back propagation，BP)神经网络算法、最小二乘支持向量机(least squares support vector machine,LSSVM)算法等，还有遗传算法、果蝇算法(fruit fly optimization algorithm, FOA)等优化算法。BP神经网络算法结构简单、可调参数多、可操作性好，但是收敛速度慢、不能保证收敛到全局最小点且网络结构不易确定。LSSVM算法收敛速度快，但是惩罚因子c和核函数参数σ需要手动选取，操作不便。遗传算法全局搜索能力强但局部搜索能力有限，一般只能得到问题的次优解，而FOA算法可实现全局自动寻优、收敛速度快，弥补了遗传算法的不足。从以上分析可知，当FOA算法与LSSVM算法相结合时，能够实现算法收敛速度快且可全局自动寻优的目的。因此，本文选用果蝇算法优化最小二乘支持向量机(fruit fly algorithm to optimized the least squares support vector machine,FOA-LSSVM)算法对扩散硅压阻式压力传感器进行温度补偿。

1 扩散硅压阻式压力传感器的工作原理

在硅膜片上采用扩散掺杂法制作4个阻值相等的压敏电阻，并且由这4个扩散压敏电阻构成惠斯登桥式测量电路。

扩散硅压力传感器原理如图1所示。

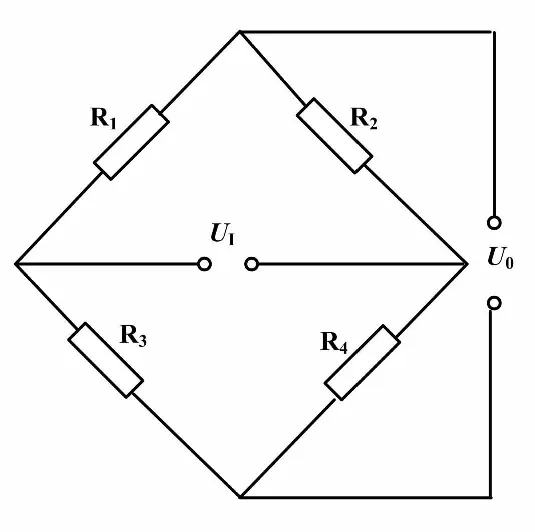
图1 扩散硅压力传感器原理图

沿着某一方向施加应力时，由于压阻效应[5]，半导体材料的电阻率会发生变化，影响电桥中电阻值的变化。当不受压力时，电桥的输出U0理论上应该为零。当硅膜片受压时，膜片的形变将使4个电阻条的阻值发生相应变化，电桥失去平衡，输出相应的电压U0。该电压U0与被测压力成线性关系，从而达到测量压力的目的。

2 FOA-LSSVM算法的温度补偿原理

2.1 LSSVM算法原理

LSSVM是由标准支持向量机(support vector machine,SVM)演变而来的。LSSVM用训练误差的平方替代SVM中的松弛变量，并用等式约束替代不等式约束，把SVM的训练转化为线性方程组的求解，再采用共轭梯度方法求解，从而避免了二次规划问题，提高了训练的速度[6-9]。

样本集{(xi,yi)}有LSSVM的回归函数：

f(x)=〈ω，x〉+b

(1)

将求解f(x)转化为求解下列方程组最优解问题：

(2)

引入拉格朗日乘子λi，构建如下拉格朗日方程，求最优解：

(3)

对式(3)求偏微分：

(4)

将式(4)的前三个方程代入第四个方程，可得：

(5)

引入高斯型径向基函数为核函数(RBF核)，核函数定义为：

(6)

以上公式中：ξi为松弛因子；c为惩罚因子；x为训练样本；x′i为SVM支持向量机；σ为核函数参数。

将式(6)代入式(5)中，可得LSSVM的回归方程为：

(7)

2.2 FOA-LSSVM算法原理

FOA是潘文超学者在2011年提出的种群体智能算法。该算法通过果蝇个体和群体简单的觅食行为来表征复杂现象[6-10]。FOA原理是果蝇通过感知周围食物浓度的大小判断自己前进的方向和距离，果蝇朝气味浓度最大的位置靠近。果蝇觅食过程中通过群体之间的信息交互作用，使得最终全部到达食物浓度最优的位置。

采用FOA-LSSVM算法对扩散硅压力传感器进行温度补偿，样本训练集x为二维标定的试验数据。用FOA算法选取LSSVM算法中惩罚因子c和核函数参数σ，提高了算法预测的速度和准确度。FOA-LSSVM算法流程如图2所示。

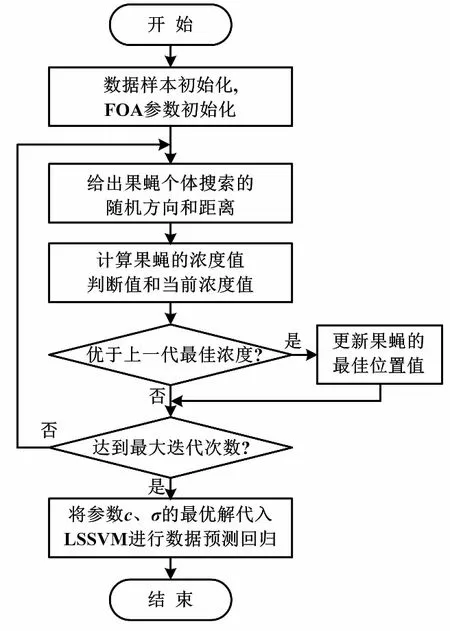
图2 FOA-LSSVM算法流程图

FOA-LSSVM算法具体工作步骤和参数设计如下所示。

①根据归一化扩散硅压阻式压力传感器二维标定试验得到的数据样本，建立训练样本数据和测试样本数据。

②初始化FOA算法参数，确定最大迭代次数gmax=300；种群规模S=20；令迭代次数g=0；果蝇的最初位置Xaxis=rand(1，2)，Yaxis=rand(1，2)；果蝇随机飞行的范围FR⊂[-10,10]。

其中：rand( )是随机数函数，rand(1，2)随机生成一个一行两列(0～1)之间的随机数。

③进化开始， 给出果蝇Fi的随机方向和随机距离：

(8)

④初步计算，计算果蝇Fi与初始位置的距离Di，就能算出气味浓度判断值Si。其中：Di由[D(i,1),D(i,2)]表示，Si由[S(i,1),S(i,2)]表示，然后根据得到的Si计算LSSVM算法的参数c和σ，如式(10)所示。

(9)

(10)

Si的计算公式为：

(11)

⑤更新后代，令g=g+1，由式(11)计算得到果蝇当前味道浓度Si。比较当前浓度值Si和当前最佳浓度值Sbest，更新整个果蝇群中的最佳味道浓度值，仍用Sbest表示，并找到其对应的最佳位置Xbest和Ybest，此时令Xaxis=Xbest，Yaxis=Ybest。

⑥迭代循环，若g≤gmax，则回到③；否则，跳出循环，记录当前的最佳位置和最佳浓度，并根据式(10)计算LSSVM算法的惩罚因子c和核函数参数σ。

⑦将数值代入LSSVM，进行数据的回归预测。

3 扩散硅压阻式压力传感器的温度补偿

3.1 二维标定试验

二维标定试验利用LM35温度传感器，THSRZ-2型传感器系统综合试验装置中的MPX10扩散硅压力传感器以及恒温箱。将温度传感器和扩散硅压力传感器一同放在恒温箱中，在不同的温度时调节压力大小，以10 kPa压强为间隔，记录不同压力下输出的电压值。本试验分别标定了21.8 ℃ 、25 ℃、30 ℃、35 ℃、40 ℃、45 ℃、50 ℃、55 ℃、60 ℃、65 ℃十组温度下电压输出。

二维标定试验原始数据如表1所示。

表1中：T为恒温箱的温度值；UT为温度传感器输出的电压值；P为气压计两个气室的差值即输入的压力值。

表1 二维标定试验原始数据

采用MATLAB对原始数据进行数据拟合，二维标定试验数据拟合曲线如图3所示。

图3 二维标定试验数据拟合曲线图

从图3可以看出，不同环境温度、同一压力输入时，扩散硅压力传感器会产生不同的电压输出，即该传感器的输出电压受到温度的影响比明显。下面用零位温度系数α0和灵敏度温度系数αs这两个指标评价温度对扩散硅压力传感器的影响。

零位温度系数α0表示零位值U0随温度漂移的速度，即温度改变1 ℃时零位值的最大改变量ΔU0m与量程U(FS)的百分比。

(12)

灵敏度温度系数αs表示灵敏度随温度漂移的速度，即温度改变1 ℃时输出电压值的最大改变量ΔUm与量程U(FS)的百分比。

(13)

以上公式中：ΔT为传感器工作环境温度改变的范围；ΔU0m为在ΔT温度变化范围内零位输出值的最大变化量；U(FS)为量程即输出电压值的最大值与最小值之差；ΔUm为在ΔT温度范围内全量程范围内同一输入条件下温度漂移的最大值与最小值之差。

依据表1中数据可以得出，ΔT=65℃-21.8℃=43.2℃；量程U(FS)=162.65 mV-5.4 mV=157.25 mV；ΔUm=162.65 mV-148.85 mV=13.8 mV；在0 kPa时，ΔU0m=8.85 mV-5.40 mV=3.45 mV；将以上数据代入式(12)、式(13)，求出零位位温度误差α0和灵敏度温度系数αs，即：

10-4/℃

(14)

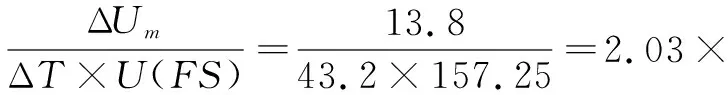
10-3/℃

(15)

由式(14)和式(15)可知，零位温度系数α0和灵敏度温度系数αs是比较大的，所以需要对该传感器进行温度补偿。

3.2 FOA-LSSVM算法的温度补偿结果分析

用MATLAB软件运行FOA-LSSVM算法对二维标定测得的数据进行数据处理，算法可得到压力预测值，从而进行温度补偿，减小误差。FOA-LSSVM温度补偿系统如图4所示。

图4 FOA-LSSVM温度补偿系统图

原始测量有11组数据，选用30 kPa和60 kPa的两组数据作为测试数据，其余的9组数据作为训练样本。选择种群规模30，迭代次数为300次，对测得的UT和UO进行回归预测训练。

FOA-LSSVM温度补偿后的压力输出值如表2所示。

表2 FOA-LSSVM温度补偿后的压力输出值

进化代数与适应度关系如图5所示。

图5 进化代数与适应度关系图

从图5可以看出，在迭代到接近50代时就找到了惩罚因子c和核函数参数σ的较优解。根据表2中数据对温度补偿后的压力值进行线性拟合，结果如图6所示。

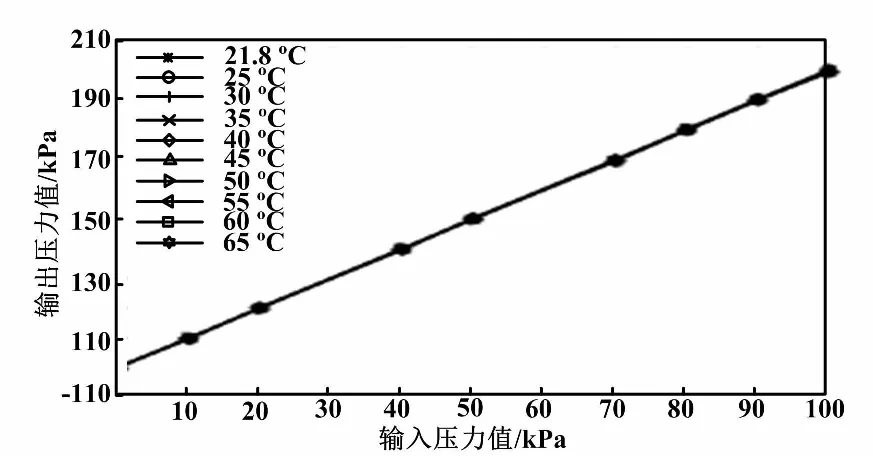
图6 温度补偿后压力值数据拟合曲线图

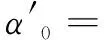
10-5/℃

(16)

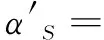
10-4/℃

(17)

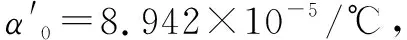
4 结论

本文采用FOA算法优化LSSVM算法的惩罚因子c和核函数参数σ，避免了LSSSVM算法手动选取参数的麻烦，从而大大提高了算法的效率和预测的准确度。采用FOA-LSSVM算法对扩散硅压力传感器进行温度补偿，其零位温度系数α0提高了一个数量级，灵敏度温度系数αs提高了一个数量级。因此，该算法对扩散硅压阻式压力传感器的温度补偿得到了理想的效果。