风电机组齿轮箱动态周期不完全维修优化

刘华新，刘红艳，罗学智，朱霄珣

(1.华北电力大学动力工程系，河北 保定 071003；2.河北软件职业技术学院软件工程系，河北 保定 071000)

0 引言

大型风电机组作为户外发电设备，其工况恶劣，运行状态受自然环境如风速、风向、温度等影响较大，停机事件频发。风电企业运维费用在发电成本中的占比居高不下。据欧洲风能理事会的统计数据显示，风电机组运维成本约占度电成本的20%～25%[1]。当前，风电场中广泛采用的维修策略为故障维修和固定时间间隔的定时维修相结合，忽视了运行时间和维修活动对设备失效率的影响，容易造成“过修”或“欠修”。“过修”会造成维修成本的浪费和加速设备的老化，而“欠修”则为重大事故的发生埋下了隐患。

齿轮箱作为大规模装机的双馈型风电机组的关键设备，承受变速变载荷和恶劣的工作环境，其故障会造成风电机组长时间停机，发电量损失较大。针对齿轮箱维修策略的研究，对降低维修费用、提高机组可用度具有重大意义。当前研究中的预防性维修模型多采用固定周期[2]或修复如新的更换维修，即“完全维修”[3]。但是对于风电机组中的齿轮箱整体进行直接更换造价高昂。故在齿轮箱全寿命周期中，一般优先采用功能恢复的“不完全维修”或仅恢复运行的“最小维修”。

本文针对齿轮箱，在每个维修周期中，如有故障发生，采用“最小维修”恢复设备运行。在每个维修周期结束时刻，采用“不完全维修”方式的预防性维修。采用役龄修正因子[4]和失效率增长因子[5]对失效率函数进行修正来表示每一次预防性不完全维修的维修效果，使其更符合设备的实际运行状态，更好地满足实际工程需要。根据实际工程实践，采用动态预防性维修周期，以全生命周期维修成本最小为目标进行优化，求解最优维护策略并进行仿真分析。计算结果表明，该模型可有效降低维修成本，优化维修周期，提高风电场的经济效益。

1 齿轮箱失效率修正模型建立

1.1 模型描述

①齿轮箱在有限的(0，Ts)时间段内运行。

② 在Ts时刻前的第i个预防性维修周期内，齿轮箱如果没有发生故障事件，则进行预防性不完全维修，功能恢复，失效率得以降低；如发生故障事件，则在故障时刻进行最小维修，失效率无变化。

③运行到Ts时刻，对部件进行更换维修，恢复如新。

基于以上描述，对模型中所用符号规定如下：Ti为第i个预防维修周期长度；hi(t)为第i个预防维修周期齿轮箱的失效概率密度函数；Ri(t)为第i个预防维修周期齿轮箱的可靠性函数；η为威布尔分布尺度参数；β为威布尔分布形状参数；αi为第i次预防性不完全维修后役龄修正因子；λ为预防性不完全维修后失效率增长因子。

1.2 模型建立

根据经典维修理论，维修可以使设备的役龄得以恢复。但是除更换外很难实现役龄完全恢复，只能回退到之前的某个时刻[6]。同时，在实际维修工作中，设备经过维修后，通常能恢复设备功能，但是会以更短的时间间隔迎来下一次预防性维修。为了使齿轮箱失效率模型更接近实际运行工况，本文在经典失效率函数的基础上，引入αi和λ对失效率函数进行修正，即当系统运行到Ti后进行预防性不完全维修。由于是不完全维修，失效率无法修复如新，定义失效率回退到本次预防性不完全维修前αiTi(0<αi<1)时刻的失效率，同时失效率函数的斜率增长为维修前的λ(λ>1)倍。

役龄修正因子αi对失效率函数的影响可以用式(1)表示。

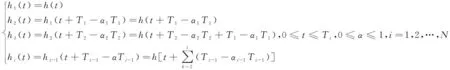
(1)

失效率增长因子λ对失效率函数的关系可以用式(2)表示。

(2)

役龄修正因子αi和失效率增长因子λ对失效率函数的综合影响可以用式(3)表示。

(3)

役龄修正因子和失效率增长因子对失效率函数的关系如图1所示。

图1 役龄修正因子和失效率增长因子与失效率函数的关系图

齿轮箱失效率服从Weibull分布[7]。Weibull分布的失效率函数为：

(4)

将式(2)代入式(1)，最终齿轮箱Weibull分布失效率函数为：

Tj≥t≥0,i=1,2,…,N

(5)

则第i个预防性不完全维修周期的可靠度函数Ri为：

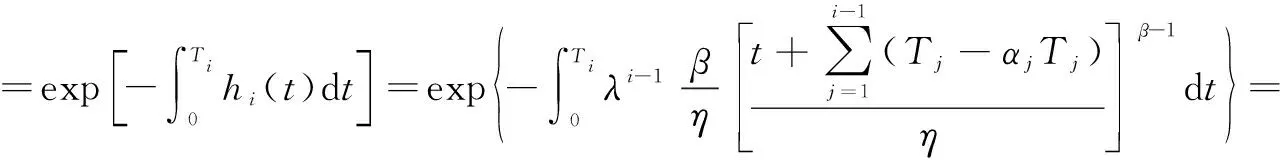
(6)

2 动态周期预防性不完全维修模型

定义C0为齿轮箱更换维修成本、Cip为预防性不完全维修成本、Cf为故障后最小维修成本、R0为可靠度最低下限。假设故障停机损失为常数，计入故障后最小维修成本，故障停机时间不计入齿轮箱全寿命周期；预防性不完全维修停机损失为常数，计入预防性维修成本，预防性不完全维修停机时间不计入齿轮箱全寿命周期；齿轮箱更换维修停机损失为常数，计入更换维修成本，第i个预防性不完全维修周期内失效次数为[8]：

(7)

第i个预防性不完全维修周期内的维修成本为：

(8)

最后一个维修周期内进行齿轮箱更换，该周期维修成本为：

(9)

齿轮箱全寿命周期的总维修成本为：

(10)

本文系统以齿轮箱全寿命周期总维修成本最小为优化目标，以可靠度Ri≥R0为约束，则优化目标函数为：

min{C∑}

(11)

约束条件为：

Ri(Ti)≥R0,i=1,2,…N

(12)

(13)

3 仿真分析

表1 可靠度限制下维修策略结果

将N=4及其他参数代入式(8)和式(9)中，可求得优化后齿轮箱预防性不完全维修累计成本为480 135.13元。与只考虑可靠度限制下累计维修成本相比，优化后的模型可以节约60 894.04元。经济成本和可靠度限制下维修策略优化结果如表2所示。

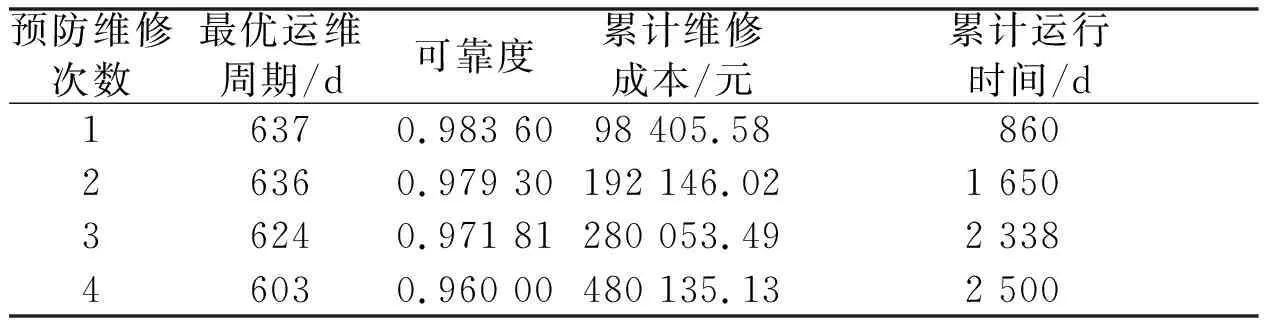
表2 经济成本和可靠度限制下维修策略优化结果

从表1和表2可知，预防性不完全维修运维周期逐渐缩短。这是由于役龄修正因子和失效率增长因子影响了其运维周期，符合齿轮箱的实际工况。预防性不完全维修最优运维周期小于最长运维周期，主要是因为最长运维周期对可靠度进行了充分运用，但是忽略了经济性的影响。最长运维周期中最后一次维修间隔过小，浪费了设备的可靠度，属于对齿轮箱的“过修”。而优化模型兼顾经济性和可靠度的相互影响，使维修周期得以优化、累计维修成本得以降低。

4 结论

本文在传统失效率函数的基础上，引入役龄修正因子和失效率增长因子，综合修正齿轮箱的失效率函数，使其更符合齿轮箱的实际运行工况。在可靠度约束下，考虑经济性的影响，建立了齿轮箱动态周期预防性不完全维修决策模型。以河北某风电场1.5 MW风电机组齿轮箱为例进行验证，优化了维修周期，降低了维修成本。风电机组其他部件也可参照此模型，建立各自维修决策模型。决策模型为风电场风电机组维修的科学决策提供理论依据。