基于STM32单片机的AES算法优化与实现

许韫韬，吕志刚，黄义国,2，李晓艳

(1.西安工业大学电子信息工程学院， 陕西 西安 710021；2.江苏无线电厂有限公司，江苏 南京 210012)

0 引言

当今社会，随着时代的不断进步，人类的科技生活已经逐步迈入信息化的时代。然而，人们在享受信息通信所带来的便利和快捷的同时，难免会遇到信息泄漏或窃取事件，保障重要信息通信的安全性已逐渐成为社会关注的热点。密码学是保证信息通信安全的有效办法之一，人们可以利用密码学中的各种数据加密算法，对一些重要的数据信息进行加密处理，从而有效提高信息的安全防护能力，降低信息在通信过程中泄露的风险，有效保护人们的信息安全[1-2]。

在实际的加解密处理中，高级加密标准(advanced encryption standard，AES)是现阶段通用的区块分组式加密标准。其硬件实现方式相对于软件实现，具有更高的物理安全性和运行速率。在密码学中，对称分组密码算法能够完成置换运算的基本结构就是S盒(substitution-box)。密码学的不断革新，推动了密码破解技术的发展。由于各种攻击方法相继涌现，AES算法在密码学的地位也受到了一定的冲击。其主要原因在于，AES算法自身仍存在不足。诸如算法结构层次上具有一定的缺陷，加、解密的结构不对称，扩展密钥的安全等级不高等[3]。针对AES算法在密钥扩展过程存在的不足，提出了一种优化方案，分别通过MATLAB仿真软件和STM32处理器对优化后的AES算法进行了研究。该算法具有很好的安全性和可靠性。

1 AES算法及优化

1.1 算法概述

AES算法又称Rijndael算法，是现阶段加密方面使用最为广泛的对称分组式算法之一[4]。AES算法的制定是为了替代已被攻破的美国数据加密标准(data encryption standard，DES)算法。AES算法在算法结构上采用的是SPN结构，通过特殊迭代密码，可以有效地抵御现有的多种密码攻击方式[5]。由此可见，AES算法的抗密码能力要远远强于被淘汰的DES算法，同时AES算法还拥有良好的可扩展性。

AES算法作为现阶段常用的对称分组式加密算法，其明文分组的长度为128位。算法在加解密处理过程中所涉及的密钥长度主要有AES-128、AES-192和AES-256三种，分别表示128位、192位、256位的密钥长度。根据矩阵形式，使矩阵中的每个字节按照由上至下和由左至右的秩序进行排列，从而构成由16个字节组成的有序矩阵。通过这种方式，构成了AES算法分组的基本结构。AES算法对语音信息进行加密和解密的处理过程，其实质是由对应的矩阵进行相应的变化实现的。在矩阵进行变换的过程中得到的中间态称为状态矩阵。对这些状态矩阵进行不同次数的迭代轮变换，可实现对信息的加密和解密处理[6]。根据密钥长度的不同，AES算法在加密以及解密的两个过程中[7]与之相应的所执行的迭代次数也不相同。三种加密算法的加密轮数如表1所示。

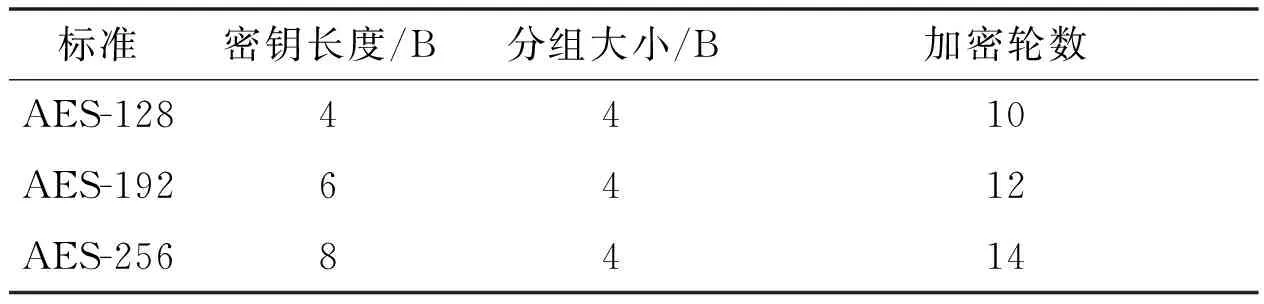
表1 三种加密算法的加密轮数

密钥长度以及分组大小在运算过程中都是以字节为单位，而每个字节的长度为32位。AES算法在进行加解密的过程中，当使用的密钥长度越长时，算法在加解密的过程中需要操作的加解密的轮数也会随之变得更多。此时相应的算法安全性也变高，但缺陷是算法的运行效率会受到影响，解密所使用的时间变得更长。所以用户需要根据实际的项目需求选择合适的密钥长度，达到相应的安全级别。由于语音数据量大、变化速率快，在确保AES算法的安全性的同时，实现尽可能高的执行效率。通过对几种算法在运行效率以及算法安全程度的对比分析，最终选择执行效率和安全性都相对较高的AES-128算法，实现对语音信息的加密以及解密操作。

1.2 密钥扩展算法

利用初始密钥进行迭代处理生成算法加解密所需要的子密钥的过程就是密钥的扩展。在这个过程中，需要用到密钥扩展算法完成初始密钥向子密钥的转换，然后将生成的子密钥应用到算法的加解密过程中。选择AES算法类型为AES-128，在完成一次明文向密文的转换过程需要执行10轮运算。但是根据实际测试发现，运算速率还是无法满足对语音数据的加密要求。通过查阅相关资料后，将10轮算法精简至6轮运算，在保证算法安全性的基础上，算法的运行速率也得到大幅提升。据此，AES算法完成6轮运算共产生896位密钥。

假定选用Wi来表示密钥矩阵K中的第i列对应的数值，根据密钥扩展算法递归得到Wi的数值完全是由Wi-1和Wi-4决定的。AES算法在进行密钥扩展的过程是依据式(1)和式(2)执行的。其扩展规则为：如果i的值不是4的整数倍时，只需要把Wi-1和Wi-4对应的数组进行异或变换就可以得到Wi；当i的数值为4的整数倍的时候，式(2)中的Wi-1需要通过函数“g”变换后得到结果，再将计算结果与Wi-4进行异或运算得到Wi。

Wi=Wi-4⨁Wi-1，i不是4的倍数

(1)

Wi=Wi-4⨁g(Wi-1)，i不是4的倍数

(2)

式中：Wi、Wi-1、Wi-4分别为密钥矩阵K中的第i列、第(i-1)列、第(i-4)列所对应的矩阵。

AES算法在完成初始密钥生成轮密钥时要用到轮常量数组Rcon[i]。它是一个4×10常量数组，同时数组的每一列均含有4个字节。其中：Rcon[i]每列的高8位均是由数组RC[i]组成，余下的位都用0补充，即Rcon[i]=(RC[i],0,0,0)。密钥扩展过程中的轮常量取值如表2所示[8]。

表2 轮常量取值

根据上述的密钥扩展过程，以W0-3作为用户设定的初始密钥，通过密钥扩展算法得到轮密钥W4-7。密钥扩展过程如图1所示。

函数“g”是经过三个基本变换得到的复杂函数，即循环移位(RotWord)、字节代换(SubWord)和轮常量异或[11-12]。若输入数据为W=(B0,B1,B2,B3)，通过RotWord变换后得到 (B1,B2,B3,B0)，再经过SubWord变换后得到(B1a,B2a,B3a,B0a)，最后通过与RC[i]异或运算得到g(W)，并将得到的结果g(W)运用于式(1)、式(2)的运算过程。

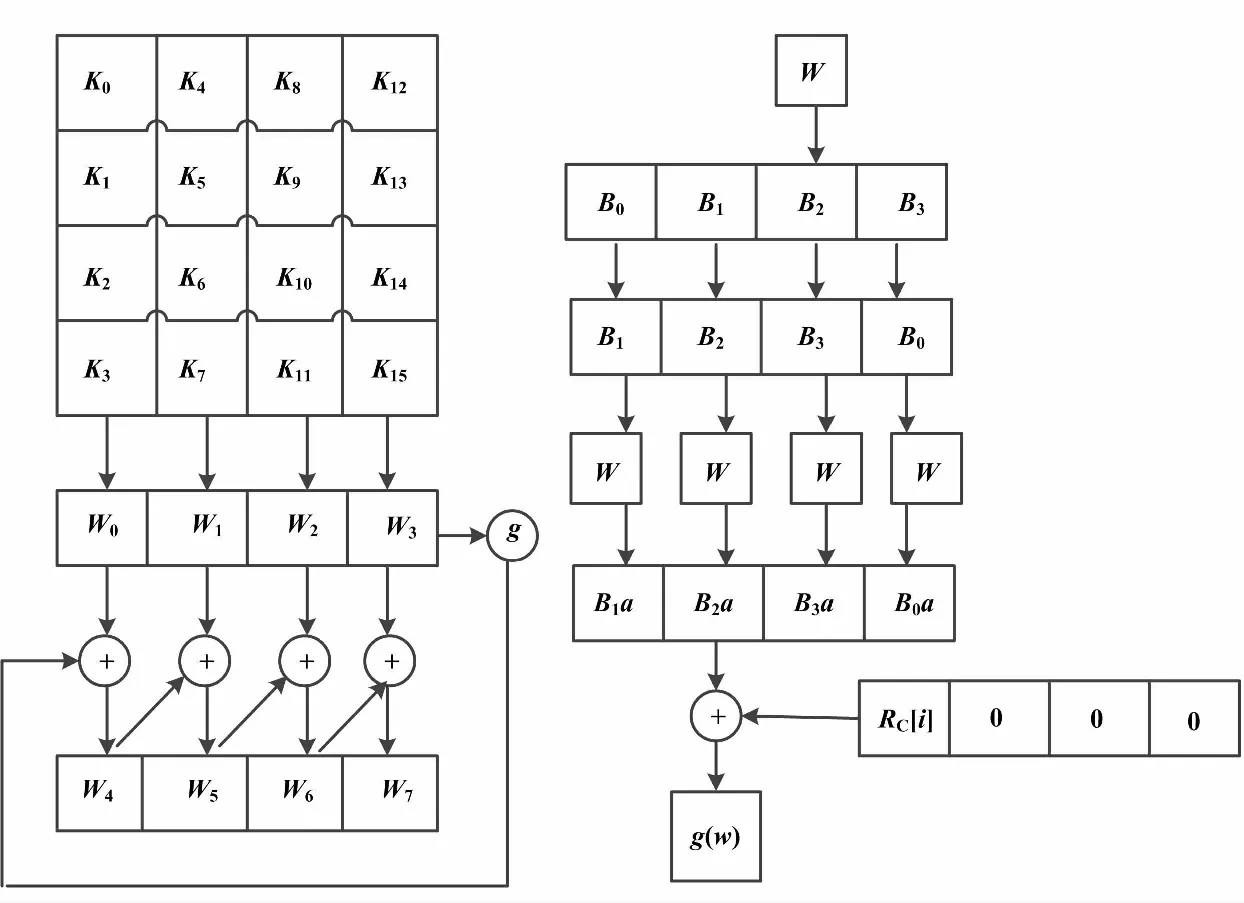
图1 密钥扩展过程图

1.3 算法优化

在加解密的过程中，AES算法对语音数据信息进行加密以及解密所使用的轮密钥均是通过初始的密钥进行扩展得到的。因为这种扩展方式的存在，导致后续所生成的轮密钥以及后续通过迭代生成的密钥都与初始密钥存在较强的关联性。这种关联性容易导致初始密钥被逆向推出来，从而造成密钥系统被破解的危险[9]。

通过查阅相关资料，并依据原始算法在对密钥扩展中存在的不足，提出了AES算法的改进方案[10]。具体的改进方案为：首先通过对初始密钥矩阵[W0,W1,W2,W3]进行行输入、列输出的置乱操作，然后生成状态矩阵[A0,A1,A2,A3]；再对状态矩阵与初始密钥矩阵进行异或变化，得到后续生成子密钥所必须的种子密钥矩阵[W4,W5,W6,W7]；最后依据原始AES算法的密钥扩展过程，以种子密钥替代初始密钥继续完成生成子密钥的操作，经过多次迭代后生成改进后算法所需要的所有的子密钥。改进后的密钥扩展过程如图2所示。

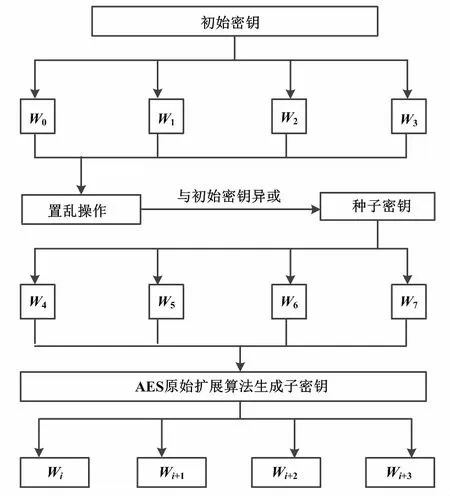
图2 改进后的密钥扩展过程图

通过改进算法与原始算法在密钥扩展的方式对比可知，改进后的算法通过对初始密钥与轮密钥进行列输入与行输出的置乱操作，可以有效降低初始密钥和轮密钥间的关联性。其次，再将置乱后的两个矩阵相异或变换。这个过程可以使得初始密钥矩阵和种子密钥矩阵之间只有对应的字之间有关联。通过对两个矩阵处理，进行异或变换可以防止出现破解的可能。最后，用得到的种子密钥代替初始密钥，经过密钥扩展生成加解密过程所需要的全部子密钥。通过分析发现，该优化方案不仅最大程度地继承了原有密钥扩展算法中的结构，而且加入的操作并没有降低算法的执行效率。

在密钥长度方面，密钥长度是由种子密钥[W4,W5,W6,W7]([W0,W1,W2,W3]与[A0,A1,A2,A3]的异或结果)决定的。因此对于破解者来说，想要利用子密钥来推导出初始的密钥，至少需要逆推232次；而想要破解整个密钥系统，攻击者至少要完成2128次穷举[11]。由此可见，改进后的方案增强了原有算法的抗密码分析能力。

在运行速度方面，由于改进的算法在原有的算法的基础上加入异或变化，而对算法的执行效率会造成一定的影响。但是在实际的运算过程中，如果只是增加了两个异或运算，在算法的整体运行速率上并不会产生太大的影响。同时，算法在处理信息的过程中，并没有涉及很深的运算，因此在运行时间方面要远小于子密钥生成所需时间。另外，由于处理的语音数据在数据量和数据长度方面相对较大，算法本身并不需要进行频繁的更换分组数据的初始密钥，可以根据语音数据的传输周期进行适当的更换。因此，相对于原始算法在对密钥扩展所使用的时间，改进后的算法在使用时间和运行效率方面都得到了很大的提升。

2 优化算法仿真分析

MATLAB是一种广泛应用于数值分析、数据处理和算法开发的高级计算机语言。MATLAB平台操作方便，同时拥有功能强大的工具箱和矩阵运算能力，在科学研究和工程设计领域都有普遍应用[12]。利用MATLAB对于数据处理的优势，实现对改进后算法的可行性的仿真分析。

在进行MATLAB仿真中，可以使用平台自带的音频读入函数wavread()直接对输入的语音样本信息进行加密和解密操作。其伪代码描述如下。

voice Path = [pathname filename];

[voice Origin,fs,bit] =wavread(voice Path);

//读入一个语音文件

Is_voice Cip(i,:) = cipher (Is_voice Origin(:,i),w,s_box,poly_mat)

//语音加密

Is_voice Recover(i,:) = inv_cipher(Is_voice Cip(i,:),w,inv_s_box,inv_poly_mat,AESIndex);

//语音解密

改进算法对语音加解密的波形如图3所示。改进算法对语音加解密的频谱如图4所示。

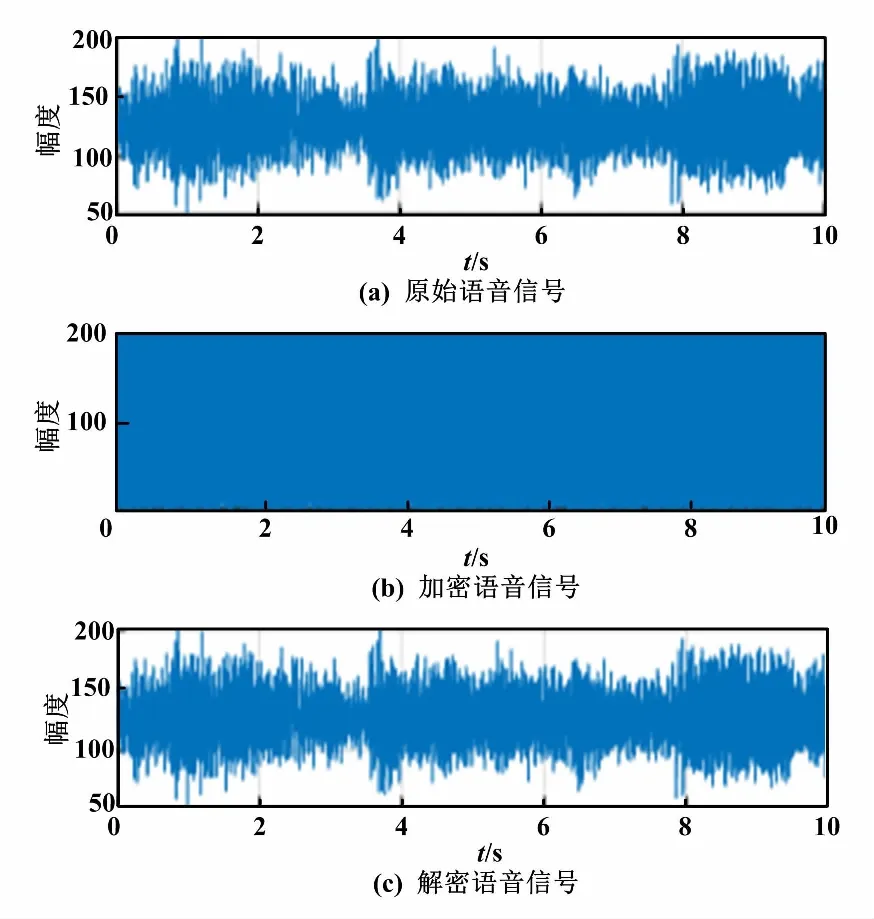
图3 改进算法对语音加解密的波形图

从图3可以看出，原始语音采样信号波形的波动变化较大，而经过改进算法加密后的语音信号被完全覆盖了，因此很好地证明优化后的算法具备较好的混淆和扩散的特性。

从图4可以看出，原始语音信号的频谱幅度变化不是很均匀，但是通过AES算法加密后，获得的密文信号的频谱较为平坦。通过AES算法对加密的信息解密后得到的语音信号的频谱与原始信号频谱基本一致，几乎保全了原始信号的全部数据量。因此可以得出，采用改进算法对语音数据加解密是可行的。改进算法在语音信号加解密过程中体现了较好的加解密特性。

3 优化算法STM32实现

为了进一步验证改进AES算法的可实施性，将其移植到STM32硬件平台上，对算法的性能和执行效率进行测试与分析[13]。在硬件平台完成AES算法移植后，通过输入语音信息并通过示波器对算法加密和解密效果进行验证。

在计算机上选取一段可视的英文字符串作为明文数据，并将明文数据发送给STM32单片机。STM32将经过算法加密后的密文数据，通过串口通信上传至计算机进行显示。计算机得到的是一串杂乱无章的密文数据。根据计算机显示的数据，需要加密的数据已经被STM32硬件平台加密。此时，再将加密的数据下发至主控芯片进行解密处理，通过硬件平台解密处理后的数据与原始数据对比发现，数据保持一致。根据试验现象分析发现，AES算法在STM32硬件平台上可以实现对字符串进行加解密的操作。通过后续对不同长度字符的硬件加解密测试，对测试数据进行对比分析发现，明文数据进行加密和解密处理后的数据与原始数据基本保持一致，验证了AES算法的稳定性和可靠性。

4 结论

针对原有AES算法在密钥扩展过程存在密钥之间关联性强的问题，提出了一种优化方案，通过对初始密钥进行置乱和异或操作，降低了初始密钥与轮密钥之间的关联性，可以在原算法的基础上提高抗密码攻击能力。在对AES算法理论进行简要阐述后，分析现代传统AES算法存在的缺陷并作出算法的改进，在原有算法基础上有效提高算法的安全性和运行效率。同时，通过MATLAB平台对改进后的算法进行仿真。结果表明，改进后的算法提高了可靠性和安全性；通过在STM32硬件平台上的实现，进一步验证了优化算法的高效性和可实施性。