一种基于频率自增的高精度谐波分析方法

张俊敏,郑植,田贇祥,卢晶

(1 中南民族大学 计算机科学学院,武汉 430074;2 中国科学院 等离子体物理研究所,合肥 230031;3 中国科学院 合肥物质科学研究院,合肥 230031)

随着非线性负载的大量使用,谐波造成的污染也越来越严重,谐波不仅会损害电源系统,甚至还会危害到人身安全,由此可见,谐波治理是至关重要的[1].对电网信号进行高精度的谐波分析,是谐波治理的重要手段.目前常见的谐波检测方法有FFT变换[2]、小波变换[3]、神经网络算法[4]等,其中FFT变换由于其易于实现嵌入式微机而被广泛使用.目前,通常采用加窗插值的方法来缓解FFT 进行谐波分析时带来的频谱泄露问题[5].适当的加权窗函数能够有效地抑制频谱泄露造成的长范围泄露[6],文献[6]用不同的窗函数对信号进行加窗分析,从而验证了不同的旁瓣特性对频谱泄露的抑制程度.而插值算法能够有效抑制频谱泄露造成的短范围泄露[7],文献[7]对离散目标频点附近的谱线群进行了充分的分析,并且考虑到了谱线分布的多种可能性,提出一种多谱线插值的频谱校正算法.对仿真信号进行分析时,谐波的次数往往是已知的,所以目前关于电网谐波分析的研究中,通常是按照基波的倍数确定各次谐波,但是在面对复杂电网信号时,无法准确地判断出各次谐波,从而导致谐波分析的不完整.

为了满足电网谐波的自动检测分析及其完整性,本文在现有插值算法的基础上提出了一种基于频率自增的高精度谐波分析方法.该方法将频率设为已知参数,通过设置合适的循环变量间隔,满足复杂电网信号的谐波分析.文中阐述了该方法的实现原理,并对其测量精度进行了验证,结果表明,该方法能够有效地运用于谐波未知的电网谐波信号检测.

1 四项三阶Nuttall窗及其特性

窗函数的旁瓣特性成为选择窗函数的重要依据,旁瓣越大则泄露越多,旁瓣衰减越快则对泄露的抑制越强.在进行加窗处理时,一般选用旁瓣峰值大且旁瓣衰减速率快的加权窗函数[8].常用的窗函数主要有汉宁窗、海明窗、Blackman窗、四项最小旁瓣窗及四项三阶Nuttall窗等,其中四项三阶Nuttall窗旁瓣衰减率为30dB/oct,且旁瓣峰值电平为-83dB,其出色的旁瓣特性使它能够适应多种谐波检测场合,因此本文选用四项三阶Nuttall窗对谐波信号进行加窗处理.

四项三阶Nuttall窗是一种余弦组合窗,其时域表达形式为:

(1)

其中bm为窗函数的各项系数,b0=0.338946,b1=0.481973,b2=0.161054,b3=0.018027.N为采样点数,n=0,1,…,N-1.

其频谱函数为:

(2)

2 四谱线插值算法

设输入某一频率信号:

(3)

对式(3)所示信号按采样频率fs以N点采样,得到离散序列:

(4)

其中Am为m次谐波幅值;f0为基波频率;φm为m次谐波的相位.

对式(4)进行加窗FFT变换处理,得到:

(5)

忽略负频点谱峰的影响,对m次谐波处进行分析得到:

(6)

其中,Δf=fs/N为频率分辨率;W(ω)为给定窗函数的频谱函数.

(7)

由式(7)确定β=g(α),亦作α=g-1(β).从而确定频率的修正公式为:

(8)

对四根谱线进行加权得到幅值修正公式为:

(9)

由式(6)得到相位修正公式为:

(10)

3 频率自增的谐波分析方法

输入如式(3)所示的余弦信号,经加窗FFT变换后,由式(8)计算出基波频率f0为:

(11)

其中k2为基波附近的幅值最大的谱线,设:

(12)

其中fi为第i次谐波处的频率,j为循环变量间隔,i=1,2,…,n.再由式(8),可得:

(13)

其中α∈(-0.5,+0.5),ki是频率fi附近幅值最大的谱线.

根据式(8)、式(9)、式(10)可对离散信号进行插值修正,得到谐波的各项参数,具体的流程图见图1.

图1 流程图

4 仿真实验分析

4.1 谐波分析方法研究

现假设输入信号x,其具体参数如表1所示,且采样频率fs=10240 Hz,基波频率为f0=50.5 Hz,采样点数N=4096.

表1 信号x的参数

对输入信号加四项三阶Nuttall窗,经FFT变换后,得到其离散信号.设置循环变量间隔,根据式(9)、式(11)得出插值修正后的信号的幅值与谐波次数的关系如图2所示.

从图2中可以观察到,各次谐波对应的幅值与表1中相应的各次谐波信号幅值的大小大体一致.该方法实现了对仿真信号内各次谐波的检测,并且相较于倍频的方式,通过循环变量间隔的合理设置,能够有效地运用到谐波未知的复杂电网信号中,从而保证对复杂电网信号完整谐波的检测分析,具有一定的实用价值.

图2 信号内谐波及其幅值

4.2 不同插值算法的比较

在仿真条件完全相同的情况下,分别对文献[9]中的四项三阶Nuttall窗四谱线插值算法、文献[10]中的六谱线插值算法以及本文提出的方法对信号x进行仿真实验，得到频率、幅值、相位的相对误差分别如表2、表3、表4所示.

表2 频率相对误差

表3 幅值相对误差

表4 相位相对误差

可以看出,本文方法的测量精度相较于文献[9]中的四谱线插值算法高出了大概两个数量级,相较于文献[10]中的六谱线插值算法,测量精度高出大约一个数量级,并且,其在次谐波处的测量精度最低能够达到10-5数量级,可见该方法能够满足谐波与间谐波的高精度检测.

4.3 基波频率波动的情形

对模拟信号进行仿真实验分析时,通常假定基波频率f0为一个固定值,然而在电网中,基波频率f0的取值往往在50∓0.5Hz附近波动,现假设基波频率的波动范围为(49.5Hz,50.5Hz),取步长为0.1Hz.现针对信号x主要次谐波进行仿真分析，得出插值修正后各次谐波在基波频率波动下的幅值和相位参数相对误差分别如表5、表6所示.

表5 各次谐波幅值相对误差

表6 各次谐波相位相对误差

可以看出,在基波频率波动的情况下,谐波的幅值及相位相对误差都能保持在一个较为稳定的数量级,如基波处,幅值的相对误差保持在10-8～10-9数量级,相位的相对误差集中在10-6～10-7数量级.由此可见该方法对基波频率波动造成的影响有较好的抑制作用,并且拥有较高的测量精度.

4.4 EAST实验运行数据分析

此前已检验了该方法对仿真信号误差分析的测量准确度,现针对真实电网信号进行仿真实验分析,实验数据来源于中国科学院先进实验超导Tokamak(EAST).通过分析EAST实验期间发生谐波电压、电流运行数据,得出信号的波形如图3所示.随即对A相信号进行加窗FFT处理,得到如图4所示的A相信号的频谱图.

图3 信号波形

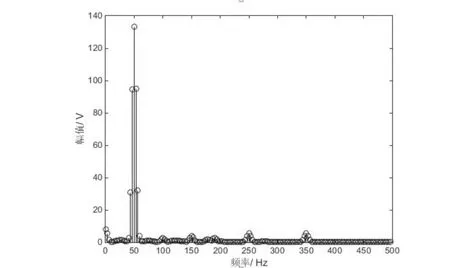
图4 信号频谱

从图4可以看出,在频率为50Hz的附近有最大谱线,该频点为基波,但是此处的频率点并非真实的谱峰频点.对此设置合适的循环变量间隔j=15,对信号进行插值修正,从而得出A, B, C三相的频率、幅值及相位分别如表7、表8、表9所示.

表7 A相参数

表8 B相参数

表9 C相参数

从表7、表8、表9中观察可知,A, B, C三相对应的频率点处的谐波信号,相位满足一定的超前、滞后关系，且表7中频率为50.00641Hz处有最大谱线,对应于图4中的基波频点,此外其余频点也都与图4各频点相对应.由此可见,设定频率按一定的步长增长,能够达到检测未知谐波的电网信号的效果.

5 总结

对复杂电网信号进行谐波检测分析时,各次谐波是未知的,若是按照基波的倍数次寻找谐波,则很可能会漏掉某一频点.针对该现象,提出了一种基于频率自增的高精度谐波分析方法,将频率设为已知参数,通过步长的合理设置,满足对电网谐波的完整分析.验证了本文方法在已知谐波次数的仿真信号下的测量精度,并与不同文献算法进行了对比,仿真结果表明:在完全相同的仿真条件下,本文方法的测量精度高出文献[9]所提算法大概两个数量级,高出文献[10]所提算法大概一个数量级.针对电网信号基波频率波动的因素,研究了基波频率在f0=50∓aHz,a∈(-0.5,0.5)下本文方法的测量准确度，并对EAST数据进行了实验分析,其实验结果能够满足电网信号的自动检测,具有一定的应用价值.