基于小波变换的图像压缩感知深度重构网络

熊承义，李治邦，高志荣，金鑫，秦鹏飞

(1 中南民族大学 电子信息工程学院，智能无线通信湖北省重点实验室，武汉430074；2 中南民族大学 计算机科学学院，武汉 430074)

2006年，DONOHO、CANDES和陶哲轩等人首次提出了压缩感知[1](Compressive Sensing，CS)理论，CS指出：假如信号本身或在某个变换域上是稀疏的，则可以通过观测矩阵将高维数的原始信号投影到一个低维空间上，并通过求解一个优化问题将原始信号以高概率重构出来.CS理论大大减少了信号的存储空间，降低了传输代价，在单像素成像[2]、医学成像[3]、无线通信[4]等领域得到了广泛的应用.

压缩感知重构是压缩感知理论中关键的问题之一，其数学模型通常可以转化为凸优化问题[5]，目前已经提出了许多传统的CS重构方法，比如交替方向乘子法[6](ADMM)、迭代阈值收缩法[7](ISTA)、快速迭代阈值收缩法[7](FISTA)和近似消息传递法[8](AMP)等.但是现有的传统优化算法主要不足之处是需要手动设置相关参数而且重构时间太长.

近年来，随着深度学习的发展，其在计算机视觉和图像处理方面受到广泛关注，并在图像去噪[9]、图像超分辨率重建[10]、图像分割[11]等领域取得了较好的效果.得益于其可以大大降低重构时间的优点，许多基于深度学习的图像压缩感知重构算法也陆续被提出.比如KULKARNI等人提出了ReconNet[12]，在一个全连接层后面堆叠两个SRCNN模型[10]，实现了非迭代图像压缩感知重构.YAO等人在ReconNet的基础上引入残差网络提出了DR2-Net[13]，网络由全连接层和四个残差学习块组成，取得了比ReconNet更好的重构效果.YANG等人提出ADMM-Net[14]，将ADMM算法映射到深度神经网络中实现，网络中参数和收缩函数等均可通过端对端的训练学习.ZHANG提出了ISTA-Net[15]，受ISTA算法的启发，将l1范数约束下的CS重构模型映射到深度网络中，采用卷积层和ReLU实现非线性变换，同时所有的参数都可以通过端到端的学习得到，并且模型可解释性强.ISTA-Net虽然在重构效果和可解释性上都有一定提升，但是其模型设计相对复杂，许多参数仍需手动设计.之后SHI等人提出了CSNet[16]，设计了卷积采样代替固定采样矩阵，不仅降低了模型设计的复杂度，而且一定程度上提高了图像的采样效率，使图像重构质量得到了进一步提升.然而，CSNet缺乏可解释性，并且在图像的深度去噪阶段和上述几种算法一样都没有充分利用图像的结构和纹理特性.

为了进一步改善图像压缩感知恢复性能，本文在ISTA-Net框架基础上，结合图像的结构和纹理特性，提出了一种基于小波变换的图像压缩感知重构网络.首先，网络引入了自适应采样，以提高图像的采样效率；其次，设计了一种梯度更新单元，对初始重构图像进行更新操作；然后对更新后的重构图像进行一阶小波变换，考虑到图像噪声主要分布在高频部分，因此保留其低频分量不变，只对三个高频分量进行去噪；最后通过小波逆变换得到去噪图像.另外，考虑到网络深度与重构图像质量之间的关系，本文将梯度更新单元和小波去噪单元进行了多次交替级联.大量实验结果比较验证了所提方法的有效性.

1 相关工作

1.1 压缩感知和传统重构算法

图像压缩感知重构主要是对图像进行随机投影采样，并利用图像在某种变换域的稀疏性作为先验知识，从少量测量数据中重构出原始图像.对于信号x∈Rn，如果它本身或者在变换Ψ对应的变换域上是稀疏的，则可以利用随机观测矩阵Φ将其投影到低维空间上，得到降维采样的测量值：

y=Φx,y∈RN,

(1)

当M≪N时，上式(1)是一个病态问题，由测量值重构原始信号会得到无穷多解.然而，压缩感知理论证明了，当观测矩阵Φ或感知测量矩阵A=ΦΨ满足约束等距时，信号x可以通过求解式(2)得到：

(2)

其中，‖*‖0表示l0范数，由于求解l0范数最小化为组合优化问题，因此式(2)是一个典型的NP-Hard问题，通常将l0范数松弛为l1范数对应的凸优化问题即下式(3)：

(3)

这是一个约束优化问题，在选择适当的正则化参数λ时，上式可进一步等价为一个无约束优化的求解问题：

(4)

对于上式(4)的求解，目前已经提出了多种方法，如AMP、ADMM、ISTA以及FISTA等.本文主要对迭代收缩阈值算法(ISTA)进行讨论.基于模型的ISTA算法将式(4)转化为下面两式的交替迭代实现求解：

r(k)=x(k-1)-ρΦT(Φx(k-1)-y),

(5a)

(5b)

上式中的k和ρ分别代表迭代次数和步长，变量r(k)代表第k次迭代运算得到的图像x的估计值，x-r(k)代表第k次迭代生成的误差图像.第一步迭代即式(5a)比较容易计算，第二步迭代(5b)的求解相对困难，然而观察发现当φ(x)=‖Ψx‖1时，式(5b)其实是一个近似映射proxλφ(r(k))，定义如下：

(6)

当φ(x)为l1范数时，上式(6)可以转换为软阈值函数实现求解.例如，取φ(x)=‖x‖1即Ψ=I(I为单位矩阵)时，x(k)=soft(r(k),λ)；若取φ(x)=‖Wx‖1，即Ψ=W(W为小波变换矩阵)时，x(k)=WTsoft(Wr(k),λ).

1.2 受ISTA启发的网络重构算法：ISTA-Net

传统ISTA算法可以方便的求解压缩感知重构问题，但是算法涉及到的所有参数均需要手动设计，而且需要多次迭代才能取得较满意的效果，重构时间太长无法满足实际应用的实时性.

为解决传统ISTA算法存在的上述问题，ZHANG等人提出了ISTA-Net[15]，其整体网络框架如图1所示，其中，x为原始图像对应的列向量，y为采样值，x(0)为初始重构图像对应的列向量.

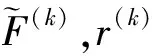
r(k)=x(k-1)-ρΦT(Φx(k-1)-y),

(7a)

(7b)

ISTA-Net与传统方法相比，不仅重构速度得到了大幅提升而且算法中的参数可以自学习；与完全基于神经网络的重构算法(如ReconNet和DR2-Net等)相比，ISTA-Net则具有更好的可解释性.然而，以ISTA-Net为代表的神经网络重构算法在对初始重构图像去噪阶段没有充分考虑图像的结构和纹理特性.

1.3 图像小波去噪原理

图像噪声来源主要可分为两个方面：图像获取过程中和图像传输过程中.常见噪声包括加性噪声和乘性噪声.假定一个噪声模型，其可以表示为：

Yij=Xijδ+N,

(8)

其中X,Y,δ和N分别表示原始图像，含噪图像，乘性噪声和加性噪声.i和j分别为像素的二维空间位置坐标.图像去噪的任务就是去除噪声，尽量找出X的估计值.小波变换能对时间和频率信号进行局部化处理，非常适合对图像进行去噪[17,18].

含噪图像经过小波变换后得到高频分量和低频分量，高频分量中包含绝大多数噪声信号，低频分量中大部分为有效信号，并且有效信号的小波分量模值大于噪声信号.因此可以选取合适的阈值从高频分量中筛选出噪声信号并置零，再利用小波逆变换恢复出干净图像，得到去噪后的图像.为了更好的恢复出图像的结构和纹理信息，本文引入小波变换并将其嵌入到深度重构网络中.

2 基于小波变换的图像压缩感知重构网络

传统优化模型的重构算法时间复杂度太高；基于神经网络的ISTA-Net虽然大大降低了时间复杂度，但是仍存在模型参数设计复杂、对图像的结构和纹理特性利用不够充分等不足.针对上述问题，本文在ISTA-Net框架基础上，结合图像的结构和纹理特性，提出了一种基于小波变换的图像压缩感知重构网络.网络框架如下图2所示，主要包括三部分：卷积采样层、初始重构层和深度重构层.

图2 本文提出方法的网络总框架

卷积采样层采用学习采样代替传统的固定基采样，通过大小为32×32的卷积核convl对输入图像进行卷积，步长取32，得到的采样输出为y.与传统方法使用固定采样矩阵进行采样相比，学习采样的卷积核conv1可以端对端学习，不仅可以避免手动设计采样矩阵而且可以提高采样效率.初始重构层输入为采样值y，y经过一个卷积核为conv2的卷积层和重组(Reshape)拼接(Concat)操作后得到初始重构图像x(0).深度重构层包含N个级联单元，第一个级联单元的输入为初始重构图像x(0)，之后每一个级联单元的输出是后一个级联单元的输入.第i个级联单元Phasei(i=1,2,…,N)对应第i次迭代操作，每个Phase又包括梯度更新单元(Gradient Update Unit)和小波去噪单元(DWT Denoising Unit)，梯度更新单元对应r(0)的更新，小波去噪单元对应r(k)的更新.

2.1 卷积采样和初始重构

针对上述问题，SHI等人提出了CSNet[16]，使用卷积采样代替传统固定基采样，本文采样和初始重构部分采用CSNet中的方法，具体实现如下图3所示.

图3 卷积采样和初始重构

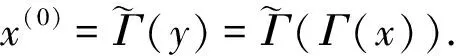
2.2 深度重构网路

深度重构网络由多个级联单元组成，每个级联单元又包括一个梯度更新单元和小波去噪单元.

2.2.1 梯度更新单元

梯度更新单元其作用是将ISTA算法中第一步交替迭代过程映射到神经网络中实现，所有参数均可自学习，避免了手动调整参数.关于ISTA算法中第一步交替迭代过程，即r(k)的迭代求解过程，传统ISTA算法和ISTA-Net均是通过式(9)实现，但是传统ISTA算法需要手动设计采样矩阵Φ，而且需要手动调整步长ρ；ISTA-Net虽然可以通过网络自学习步长ρ，但仍需要手动设计采样矩阵Φ.

r(k)=r(k-1)-ρΦT(Φr(k-1)-y),

(9)

针对此问题，本文设计一种梯度更新单元，把式(9)的求解过程映射到神经网络中实现，如下图4所示.

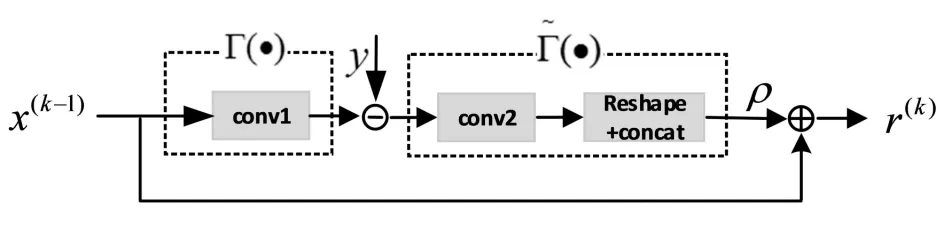
图4 梯度更新单元

梯度更新单元的输出为r(k)，输入为前一个级联单元的输出r(k-1)，所以梯度更新单元可表示为：

(10)

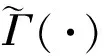
2.2.2 小波去噪单元

文献[15]提出了换向流反应器一维数学模型的一种理论解析方法与2种不同的数值计算方法，并将这3种不同求解方法与试验数据进行了对比，认为解析法在处理实际问题过程中更容易，更具有优势。

与ISTA-Net不同，本文采用小波去噪代替其原来的软阈值去噪，以期获得图像更好的纹理信息.小波去噪单元如下图5所示：

图5 小波去噪单元

小波去噪单元的输入r(k-1)为梯度更新单元的输出图像，r(k-1)首先经过一级小波变换分解为一个低频和三个高频分量，由于图像噪声主要分布在高频部分，因此保留其低频分量不变，分别对三个高频分量进行去噪.具体操作为将高频分量依次通过第一个卷积层、非线性变换层(ReLU)和第二个卷积层，其中第一个卷积层包含32个3×2×1的卷积核，第二个卷积层包含1个3×3×32的卷积核.最后将三个经过去噪处理的高频分量和未经处理的低频分量通过小波逆变换得到输出图像x(k).

3 网络训练

3.1 训练数据制作

本文使用和ISTA-Net相同的训练集，共91张图片.不同的颜色空间对图像分类、图像分割有一定的影响，但对图像重构方面影响较小.为公平起见，本文采用与ISTA-Net相同的颜色空间，将RGB图像空间变换到YCrCb图像空间，选取亮度通道，对图像进行取块操作，块大小为32×32，并对图像进行翻转旋转等操作最终得到88912个训练图像块.本文使用了7种采样率对网络进行了训练，分别是0.01、0.04、0.1、0.25、0.3、0.4、0.5，并在Set11[12]数据集上进行了测试.

3.2 训练参数设置

本文使用TensorFlow深度学习开源工具训练网络，所有实验均在Inter(R) Xeon(R) Gold 5118 CPU，主频2.3GHz内存128G，显卡GTX 1080Ti平台下完成.本文选择批次大小为64，共迭代100轮，前2轮迭代选择较大的学习率0.001，之后迭代的学习率全部设置为0.0001.所有卷积层的权重均使用Xavier方法进行初始化，偏置初始化为0.

3.3 损失函数

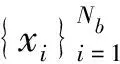
(11)

(12)

所以，总的损失函数：

L=L(1)+λL(2).

(13)

其中Nb为训练集的图像总数，N为深度重构网络的级联数，本文中N=9，NB为训练集中图像块的大小，本文中NB=32，λ为正则化参数，本文中取λ=0.01.

4 实验结果

本文与已有的5种算法进行比较，分别是ReconNet[12]、DR2-Net[13]、ADMM-Net[14]、ISTA-Net[15]和ISTA-Net+[15].首先为了验证深度重构网络中的级联单元数对重构质量的影响，本文在Set11数据集、采样率为0.25条件下和ISTA-Net+做了相应对比实验，如下图6所示.可以发现，随着N的增加，两种方法的重构效果均有所提升，并且当N分别为5、7、9、11、13、15时，本文重构效果均优于ISTA-Net+.当N=9时本文方法已经取得了良好的重构效果，N大于9时，重构质量的提升不再明显，因此本文后面所有实验均取N=9.

图6 不同级联单元数时本文算法和ISTA-Net+的平均PSNR(dB)

为了比较不同重构算法的重构质量，上表1给出了6种不同重构算法在Set11数据集上不同采样率下的平均PSNR.由表1可看出，本文算法的重构图像质量在表1的六种算法中表现最佳，特别是在较低采样率下.比如，在采样率为0.01的情况下，本文算法的平均PSNR比ISTA-Net+高2.77 dB，比DR2-Net高2.67 dB.

表1 不同重构算法在Set11数据集上的平均PSNR

为了比较不同重构算法的主观视觉效果，本文给出了0.25采样率下三幅图像的重构图像局部2.5倍放大图，如图7-9所示.观察重构结果可知，本文算法重构图像的结构纹理更加清晰.

图7 0.25采样率下不同算法对lena256重构结果

图8 0.25采样率下不同算法对Monarch重构结果

图9 0.25采样率下不同算法对Boats重构结果

5 结语

针对图像压缩感知重构问题，提出了一种基于小波变换的图像压缩感知重构网络.不仅引入了自适应采样，以提高图像的采样效率，而且设计了一种梯度更新单元，对初始重构图像进行更新操作.并对更新后的重构图像进行一阶小波变换，保留其低频分量不变，对三个高频分量进行去噪，最后通过小波逆变换得到去噪图像.实验结果表明，本算法的图像质量优于几种对比算法，验证了方法的有效性.