基于无差异阈值的停车设施定价模型

张新洁， 关宏志， 朱俊泽

(1.内蒙古科技大学土木工程学院，包头 014010；2.北京工业大学建筑工程学院，北京 100124)

停车设施在城市交通系统中具有很重要的作用，一些理论和实证研究表明，其收费定价对出行者的出行方式、路径、出发时刻和停车设施等选择行为有着显著的影响[1-3]，因此，停车收费政策的制定具有非常重要的现实意义。

在停车收费定价方面，Hensher等[1]研究了在中央商务区(CBD)内，停车价格和停车时间对出行者是否选择开车和是否选择停车的影响。关宏志等[4]通过调查分析了北京市繁华区出行者方式选择和停车行为选择与停车收费的关系。Qian等[5]研究了早通勤背景下的停车收费策略的经济性。Zhang等[6]研究了早通勤出行者出行行为随道路收费和停车收费费率的变化情况。王建军等[7]提出的停车定价方法不仅考虑了停车者和经营者的利益，也考虑了社会公众的需求。除了路外停车设施，一些研究还分析了路边停车和停车换乘(P+R)设施等多种类型停车设施的最优定价机制，此外，还有一些研究是关于垄断、寡头竞争、完全竞争等不同市场机制下的最优定价机制问题。如Wang等[8]研究了线性城市停车换乘(P+R)设施的最优选址与定价问题。卢晓珊等[9]建立了基于分层Logit模型的方式选择模型，讨论了4种机制下的收费策略。范文博等[10]研究了公共停车设施和停车换乘设施在三类运营机制下的定价问题。然而，上述代表研究中均存在以下不足：研究中对出行者出行行为的描述多采用离散选择模型，这类模型以随机效用理论和个人出行效用最大化为基本假设，这种假设可能与现实情况不符。

在另外一方面，根据诺贝尔经济学奖获得者Simon[11]提出的有限理性满意决策准则，人们的选择往往不是最优结果，而是一个满意的或其认为最优的结果。Krishnan[12]提出了无差异阈值的概念，指出只有当两个备选方案的效用差大于无差异阈值时，决策者才可以被认为是效用最大化的追求者。Lioukas[13]在Krishnan研究的基础上，建立了适用于两种以上备选方案的δ-Logit模型。Wang等[14]构建了交通需求不确定条件下的有限理性方式选择模型。张新洁等[15]认为以上有限理性Logit模型存在IIA (independence form irrelevant alternatives)特性，进而推导了能够克服IIA特性的有限理性分层Logit模型。上述研究对随机效用最大化假设进行了扩充，但是目前尚未有研究涉及无差异阈值对停车设施最优定价的影响。科学合理的出行行为假设是交通管理政策能够实现其预期目标的保证，因此在制定停车设施最优定价时考虑无差异阈值，可以更加准确地预测出行者的出行需求，进而使收费策略的制定能够更好地诱导出行者的出行行为。

本文假设所有停车场由同一个已获得政府授权的公司统一经营，政府制定停车收费的上下限，将停车设施定价问题描述为一个双层决策博弈问题，建立了基于无差异阈值的停车设施最优定价双层规划模型。双层规划模型中上层模型的目标函数是最大收益和最佳车位占用率，下层方式选择模型采用文献[15]中基于有限理性的分层Logit模型，即假设若两种交通方式的成本差大于无差异阈值，出行者的选择服从随机效用最大化；当方式间的效用差小于无差异阈值时，出行者将不能区分两者的大小，此时其方式选择是随机的。

1 模型的基本假设

如图1所示，假设出行者有三种备选交通方式从出发地到目的地，分别是全程驾车、地铁直达和停车换乘。建立如图2所示的分层结构，在出发地，即水平2，一部分出行者选择开车，一部分出行者选择地铁直达；在水平1，开车的出行者在具有相似性的全程驾车和停车换乘两种方式间做出选择。

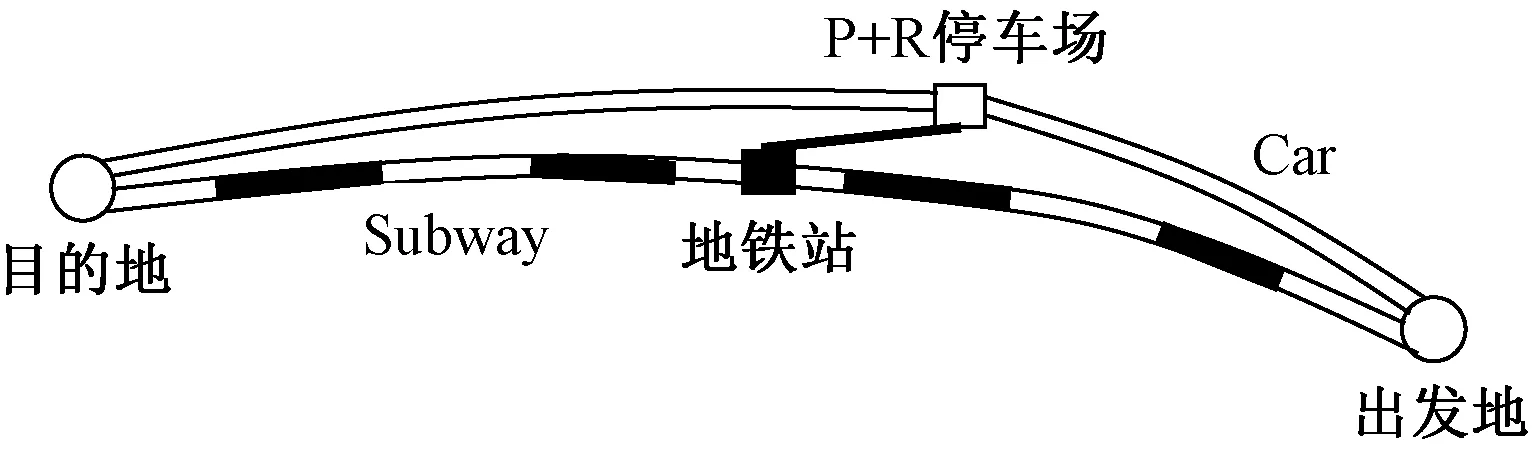
图1 多方式网络图Fig.1 Multimode network

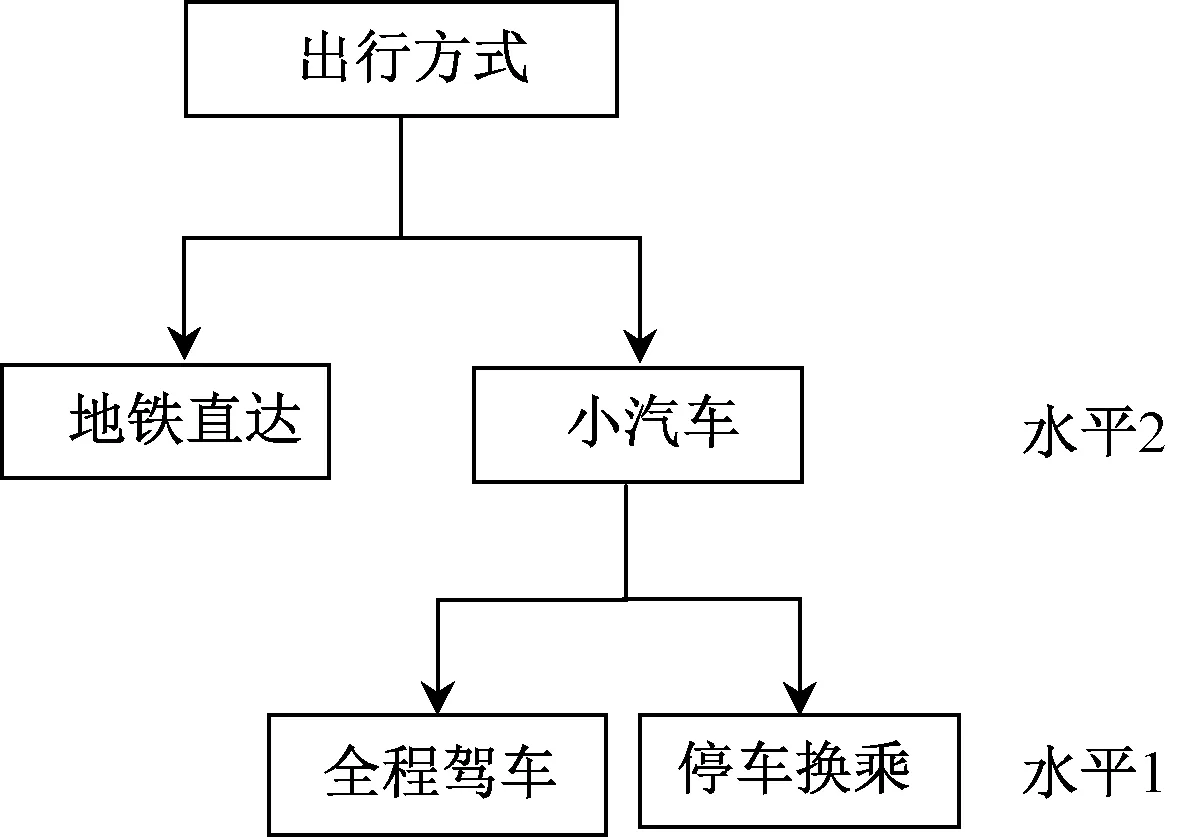
图2 交通方式的分层结构Fig.2 Nested structure of travel mode

对模型做出如下假设。

假设1停车换乘处和目的地分别设有一个停车场，假设所有停车场由同一个已获得政府授权的公司经营，政府制定停车收费上下限，运营者来制定停车设施的收费定价。

假设2交通方式的感知成本由固定项和随机项组成，随机项服从二重指数分布，且出行者是有限理性的，即当方式间的成本差大于无差异阈值，出行者的选择将服从随机效用最大化；若方式间的效用差小于无差异阈值，出行者将不能区分两者的大小，此时其方式选择是随机的。

2 基于有限理性的方式选择建模

根据文献[15]，可以写出不同交通方式的选择概率公式。全程驾车和停车换乘被选择的概率P(car)和P(PR)可表示为

P(car)=P(C)P(car|C)

(1)

P(PR)=P(C)P(PR|C)

(2)

式中：P(C)表示小汽车被选择的概率；P(car|C)和P(PR|C)分别是小汽车被选择条件下全程驾车和停车换乘的选择概率，数学表达式分别为

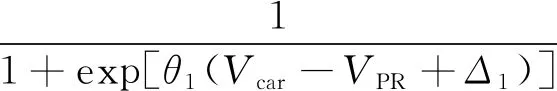
Δ1>0，θ1>0

(3)

Δ1>0，θ1>0

(4)

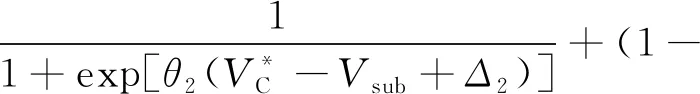
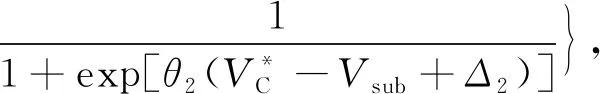
Δ2>0，0<θ2<θ1

(5)

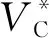
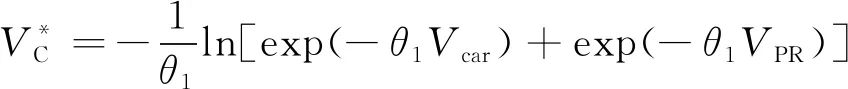
(6)

式中：Vcar、VPR和Vsub分别是全程驾车，停车换乘和地铁直达的广义出行成本；θ1、θ2是离散系数；Δ1是出行者可以区分全程驾车和停车换乘两种方式成本大小的无差异阈值；Δ2表示出行者可以区分小汽车和地铁成本大小的无差异阈值，假设所有出行者的无差异阈值都相同，Δ1≥0，Δ2≥0；τ1=τ2=0.5 表示出行者在方式间随机选择。

3 考虑车位占用率的停车设施定价模型

通过建立基于无差异阈值的停车设施定价双层规划模型来确定最优停车收费价格，上层模型的主体运营者设置停车费，下层模型的主体出行者依据运营者设置的停车费进行交通方式的选择。

根据前述假设条件，所有停车场由一个政府授权的公司运营，根据已有研究[16-17]可知，若停车设施能保持最佳的车位占用率(一般为60%～80%，理想值为85%)，能有效减少车辆的寻泊时间，避免出现供需失衡的现象。因此，在上层模型中，决策者的目标是最大收益和最佳车位占用率，停车场容量和政府制定的收费价格上下限作为约束条件，此时，上层模型是一个多目标优化问题：

0≤xk≤Hk

(7)

进一步，采用线性加权组合法，将上述多目标优化问题转化为单目标优化问题。

0≤xk≤HK

(8)

式(8)中：φ和η是权重系数，表示各个目标的重要程度；ψ是车位占用率和费用的换算系数。

4 求解算法

该双层规划问题采用遗传算法进行求解，并用套嵌相继平均算法求解下层方式选择模型，步骤如下。

步骤1遗传算法种群的初始化。根据收费的上、下限给定一组初始的停车收费方案。

步骤2求解下层模型。将初始的停车设施定价代入下层方式选择模型，用套嵌的相继平均法求解方式选择问题，确定不同停车设施定价方案下各方式的选择概率和交通量。

步骤3个体适应度函数评价。根据不同停车设施定价方案所确定的各方式交通量，计算不同定价方案下的适应度函数。

步骤4遗传操作。更新停车设施定价方案，计算相应定价方案所对应的方式选择情况，并对新种群的个体适应度值进行评价。

步骤5若算法达到最大的迭代次数，则输出优化结果；否则转步骤3。

5 数值算例

5.1 算例背景

如图3所示，以某通勤廊道作为算例背景，出行者有三种方式从出发地到目的地，分别是全程驾车，停车换乘和地铁直达。

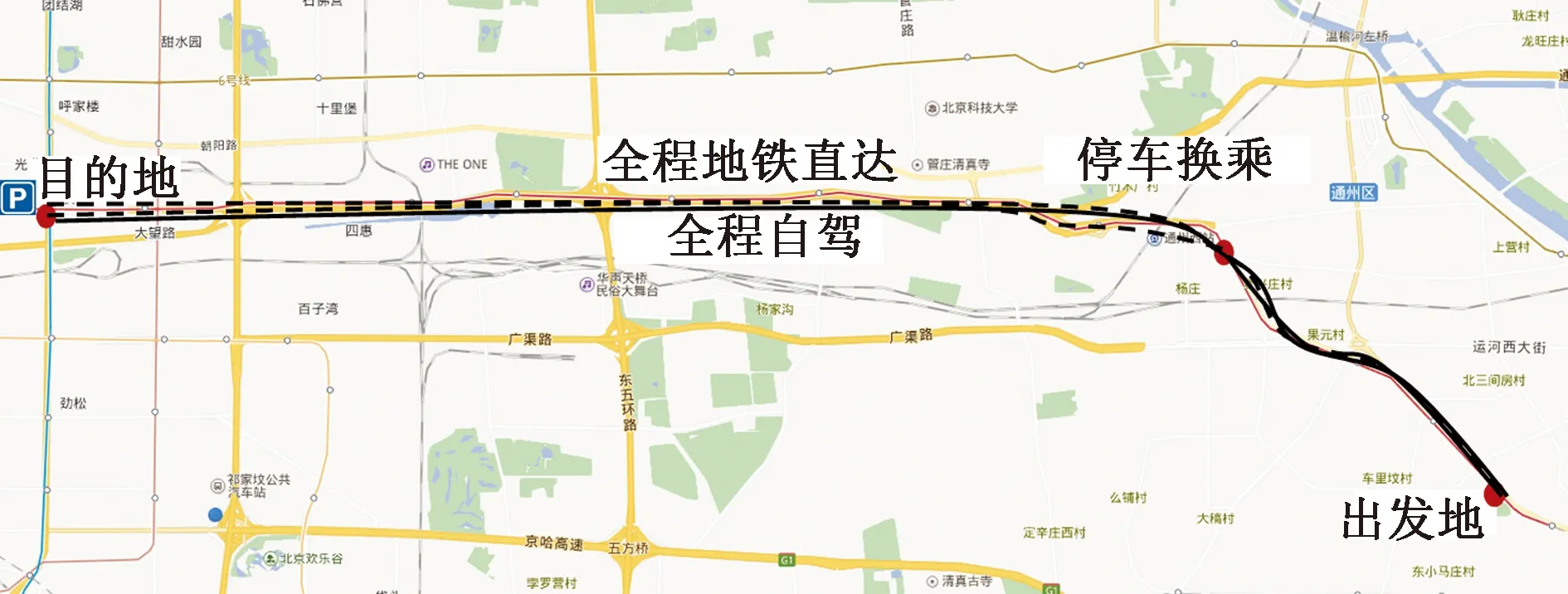
图3 某通勤廊道Fig.3 Acommunication corridor

5.2 交通方式的广义出行成本

地铁直达、停车换乘以及全程驾车的广义出行成本Vsub、VPR、Vcar分别为

Vsub=α1Tsub+μ[g(xsub)+g(xsub+xPR)]+F1

(9)

VPR=α2TPR+μg(xsub+xPR)+A+F2+pPR

(10)

Vcar=α3Tcar+ca(xcar)+A+pcar

(11)

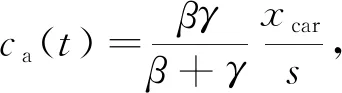
5.3 模型中参数的设置

根据文献[6，9]对模型中的参数进行赋值，如表1所示，其中D为起讫点间的总需求。

表1 模型中参数的取值

5.4 模型求解结果分析

图4所示为最优定价随Δ1的变化情况，可以看出以下结果。

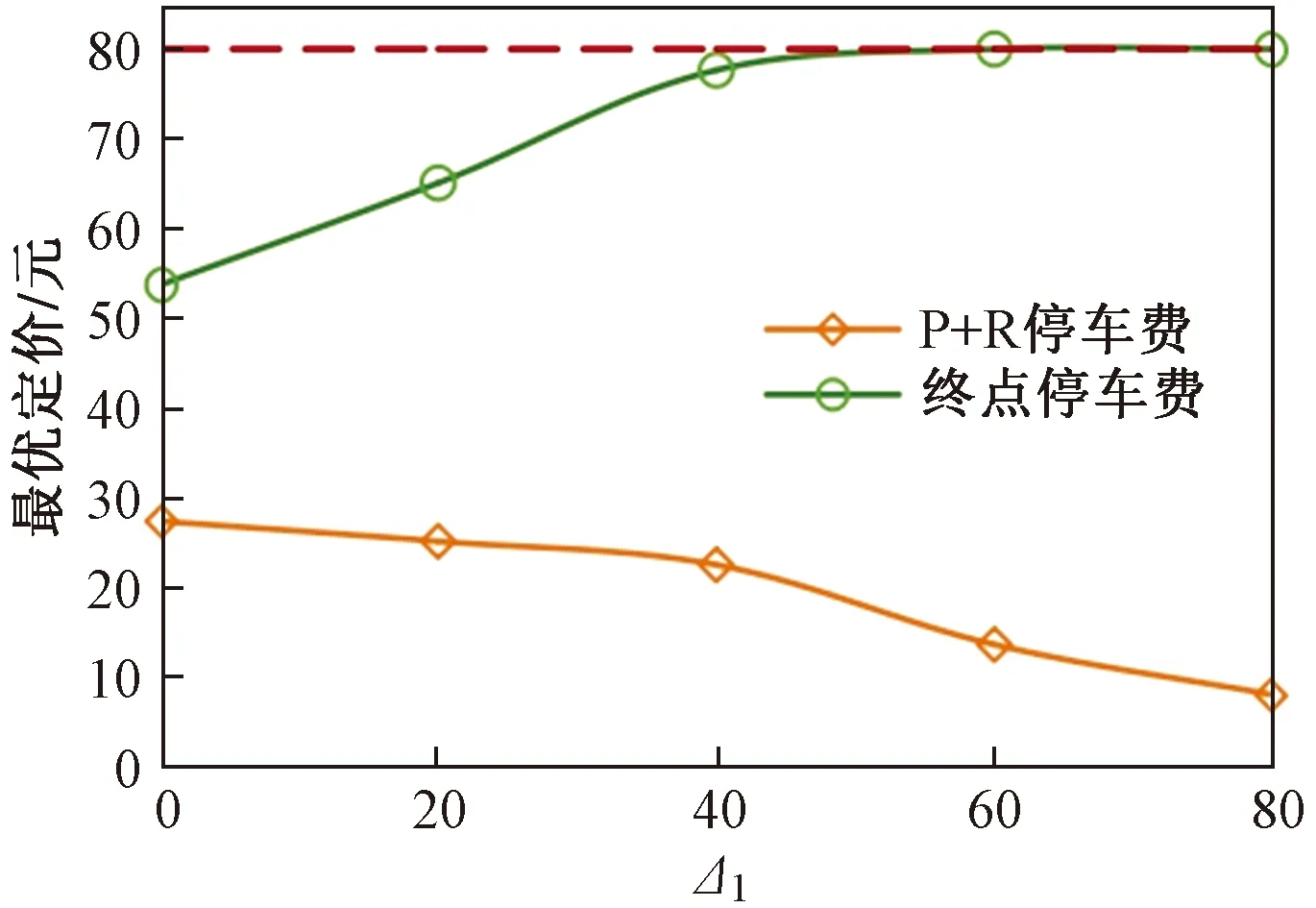
图4 Δ1对最优定价的影响(Δ2=0)Fig.4 The effects of Δ1 on optimal pricing (Δ2=0)

(1)终点停车场的最优定价随Δ1的增加而增加，P+R停车场的最优定价随Δ1的增加而减少，这是由于当Δ2=0时，出行者对于小汽车出行费用的变动很敏感，如果两个停车场都采取提高定价的策略，会导致出行者向地铁转移而引起停车场收益的减少。

(2)随着Δ1的增加，两个停车场的最优定价的差增加，是因为Δ1越大，出行者对全程自驾和停车换乘两种方式出行费用的差越不敏感。

(3)终点停车场的最优定价增加到系统设定的上限80元/次时不再增加。

图5所示为最优定价随Δ2的变化情况，可以看出以下结果。

图5 Δ2对最优定价的影响Fig.5 The effects of Δ2on optimal pricing

(1)Δ1=0时，考虑出行者有限理性(Δ2≠0)时的最优定价高于不考虑有限理性(Δ2=0)时的最优定价，且随着Δ2的增加，两个停车场的最优定价都先增加，这是因为与完全理性的出行者相比，有限理性的出行者对于出行方式费用的变动更不敏感，且Δ2越大越不敏感，因此经营者可以制定更高的定价来获取更多的收益。

(2)P+R停车场的最优定价增加到系统设定的定价上限时不再增加。

(3)终点停车场的最优定价出现降低，是因为终点停车场的占用率低于期望车位占用率，所以终点停车场需要降低其定价，吸引更多车辆，使停车资源的利用更加合理。

图6、图7分别表示不考虑无差异阈值(Δ1=Δ2=0)和考虑无差异阈值(Δ1=0,Δ2=40)时，地铁出行成本增加时，最优定价的变化情况。可以看出以下结果。

图7 地铁成本增加对最优定价的影响(Δ1=0,Δ2=40)Fig.7 The effects of the increase in subway cost on optimal pricing (Δ1=0,Δ2=40)

图6 地铁成本增加对最优定价的影响(Δ1=Δ2=0)Fig.6 The effects of the increase in subway cost on optimal pricing(Δ1=Δ2=0)

(1)无论是否考虑出行者的有限理性，随着地铁出行成本的增加，最优定价都先增加，这是由于当地铁成本增加时，停车场运营者可以通过提高定价来增加运营收入。

(2)P+R停车场的最优定价增加到系统设定的定价上限时不再增加。

(3)随着地铁成本继续增加，终点停车场的最优定价开始降低，这是因为终点停车场的车位占用率过低，需要降低定价来吸引车辆，均衡停车资源的利用。

图8表示不同定价策略下的车位占用率。权重系数η=0表示目标仅为收益最大的定价策略，权重系数η=60表示目标是同时保证停车场收益最大和实际车位占用最优的定价策略。从图8中可以看出，无论是否考虑出行者的有限理性，权重系数η=1时，两个停车场的车位占用率都比权重系数η=0时更接近期望占用率85%，说明考虑车位占用率的定价策略，能够使停车资源的利用更加合理。

图8 不同定价策略下的车位占用率Fig.8 Parking occupancy under different pricing strategies

6 结论

在考虑有限理性条件下，无差异阈值的大小会影响停车场的最优定价。

(1)Δ2=0时，终点停车场的最优定价随Δ1的增加而增加，P+R停车场的最优定价随Δ1的增加而减少。

(2)Δ1=0时，考虑出行者有限理性(Δ2≠0)时的最优定价高于不考虑有限理性(Δ2=0)时的最优定价。

(3)无论是否考虑出行者的有限理性，考虑车位占用率的定价策略，都能够使停车资源的利用更加合理。

(4)未来还可以在以下方面进行拓展研究：①考虑多种市场机制下的定价策略；②考虑不确定条件下的方式选择和定价问题。这两方面将是下一步研究的重点。