计算教学的迷失与回归

游小云

一、问题的提出

我国数学课程一直将数的运算作为小学数学的主要内容，重视培养学生的运算能力，并取得了许多宝贵的经验。小学阶段的整数、小数和分数四则运算及混合运算为以后中学学习有理数运算、整式运算打下基础。但长期以来，一些教师对计算教学的理解有所迷失，将其等同于运算技能培训（看谁算得又对又快），且由于考试等“功利性”因素，对计算速度的要求越来越高。除了运算技能，还有哪些有价值的内容？为了了解计算教学现状，笔者调研了苏州市C校各年级200名学生。本次测试内容选用与书本同等难度的练习题，如口算20以内的加、减法，表内乘、除法，笔算小数乘、除法等，并选取了淑女班（全部为女生）和实验班（传统男、女生混合班）进行对照。数据汇总如下：

笔者经过初步分析发现，低年级阶段，女生的计算速度、优秀率及合格率整体上高于男生。但到了中、高年级，女生的计算优秀率整体上低于男生，主要原因在于女生的四则混合运算分析能力、简便计算意识弱于男生。

通过访谈个别学生，笔者发现，在教学过程中教师窄化了运算能力的理解，学生对运算的意义及四则运算之间的关系、估算和精确计算的策略、运算律及运算性质没有充分理解，数学思维能力也没有得到应有的培养。

二、计算教学的迷失

什么原因导致了这样的结果？笔者经过深入调查研究，发现了计算教学的几个误区：

1.学生缺乏对算理算法的理解

笔者访谈学生对“三位数乘两位数”“小数乘除法”等精确计算是怎样想的、为什么这么算、这样算的好处等问题，学生认识不清晰。实践证明，学生在掌握知识时，如果没有理解意义，那么，知识在被淡忘以后，就很难留下什么;如果学生在学习知识时理解了它的意义，即使知识已被遗忘，能力也可以永远融合在对知识的理解之中。

2.计算教学过分依赖情境

教师忽略了学生的迁移应用，情境设置甚至显得牵强附会，情境变成看图说话，教师一味问“从图中你知道哪些信息”，削弱了数学课堂的探究味。

3.过分追求算法多样化

教师对算法只求量上的多，而忽视了学生思维品质的提升。当算法出现多样化时，教师没有引导学生对多种算法进行分析思辨，各种算法之间缺少联系。

4.计算教学缺少对话互动

计算教学表现为一种存储行为，“数学知识被看作教师给予学生的一种恩赐”，学生是知识的保管人，教师是储户。教师不是和学生进行交流互动，而是单方面灌输，让学生去接受、记忆和重复模仿，抹杀了学生在教育过程中的主动性和创造性。

三、计算教学的回归之途

鉴于上述分析，笔者认为，教师必须重新审视小學数学计算教学，学习我国传统计算教学的精髓，培养学生的计算兴趣，提高运算技能，发展数学思维能力。

1.理解算理算法是计算教学的“根”

什么是算理？什么是算法？这些是进行数学教学必须搞明白的问题。算理就是计算过程中的道理，解决为什么这样算的问题。算法就是计算的方法，解决怎样算的问题。布鲁纳认为：“学习结构就是学习事物是如何关联的。”如9.6÷3，教师要引导学生讨论商的小数点为什么要和被除数的小数点对齐，使学生明确，因为第一次是把9个1平均分成3份，每份得到3个1，所以3应该写在个位上;第二次再把6个0.1平均分成3份，每份得到2个0.1，所以2写在十分位上;最后把两次分的结果合起来就是3.2，这就是算理。把分的过程一步一步记录下来的除法竖式，就是算法。教师组织学生探索算理算法“过程和结果”的联系，使学生最终理解算理，掌握算法。

2.培养计算品质是计算教学的“道”

《现代汉语词典》对“品质”的解释为：“行为、作风上所表现出来的思想、认识、品性等的本质。”品质有很多种，工作时表现出来的是工作品质，学生计算时表现出来的是计算品质。计算品质的培养主要从计算的正确性、熟练性、灵活性和简洁性四个方面进行。学生计算的正确性和熟练性属于基础目标，即学生必须掌握应知、应会的知识和方法。计算的灵活性和简洁性属于发展性目标，应当结合学生的实际情况进行分层教学。计算品质的形成主要是建立“立体式”算法，即估算在前、笔算在后、发展口算、方法验证的立体计算模式。如3.6×2.8，教师先让学生估计结果的区间范围，在学生说出结果比6大、比12小后，让学生明确估算的理由;然后引导学生探索笔算的算理算法，学生在笔算结束后，看看笔算结果是否在估算值范围之内;最后引导学生进行验算，养成验证的习惯。

3.促进数学思考是计算教学的“魂”

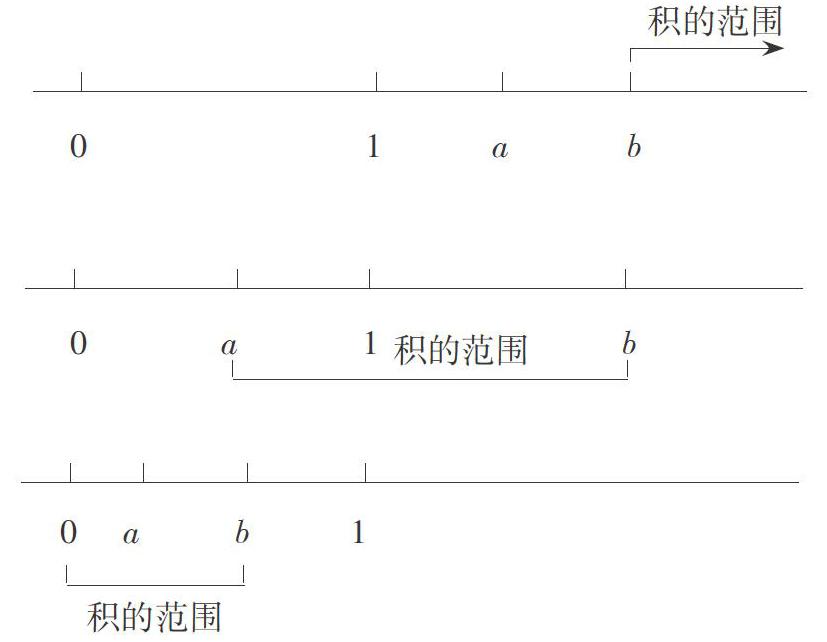
“数学思考”是从数学的角度去思考问题，发现计算现象背后的数学规律，并运用数学思想和方法去解决问题。学生探索知识的思维过程总是从解决问题开始，又从问题解决中得到创生和拓展。如在学习小数乘法的过程中，C同学发现：小数乘小数，积的变化规律富有多样性，有时积比两个因数都大，有时积比两个因数都小，有时积比其中的一个因数大，比另一个因数小。那么，在小数乘小数中，积的变化规律是怎样的呢？为了理解因数和积的范围关系，在笔者的引导下，C同学画出了下面的关系图，只要比较a、b这两个因数与1的大小就可以确定积的范围。

总之，走出计算教学的误区是一个长期的过程。只有理解算理算法、培养计算品质、发展数学思考这三个策略统一起来，计算教学才更有实效性和长效性。

（作者单位：首都师范大学教育学院）