区域水电市场价格预测模型研究
2020-08-01赵珊霈
赵珊霈
(中国电建集团北京勘测设计研究院有限公司,北京 100024)
1 概 述
电力价格是水电市场中较为重要的因素之一,是电力能源供需关系之间相互作用的结果。同时,水电市场中的电力价格还受到其他类型电力企业的影响,因而电力价格受到多种因素的影响。水电市场中的电力价格对于资源重新分配,维护供应计划,降低财务风险,制定电力市场预算和计划都至关重要,因此对水电市场中电力价格的预测模型研究具有非常重要的意义[1-2]。
在过去的15-20年中,国内外科研工作者用多种方法进行电力价格预测,取得许多较为满意的结果。 但到目前为止,这些模型的分类尚无统一的标准[3-4]。其中,较为流行的分类结果将电力价格预测模型划分为4类,分别为市场均衡模型、智能模型、统计模型、混合模型[5]。市场均衡模型主要有纳什均衡模型、SFE模型等,该类模型以社会效益最大作为均衡状态,会造成模型的预测值整体偏高。智能模型主要有智能进化模型、人工神经网络模型等,该类模型容易陷入局部最优解,影响最终预测结果的准确性。统计模型主要有自回归模型、移动平均模型等,该类模型对原始数据的依赖较大,对数据的波动不能很好地处理。混合模型主要是通过权重或者技术将上述3类模型进行组合,但是不同模型的组合未必能够提高模型的性能,需要进行大量数值模拟实验进行甄别,这无形加大预测过程的工作量。
灰色模型是一种研究“贫信息”、“小样本”和不确定性问题的方法[6-7],被广泛应用于经济、金融等领域。电力价格的历史数据量不大,同时受到多种因素的影响,具有震荡性,因此采用灰色模型对电力价格进行预测具有一定适用性。分数阶灰色模型将模型阶数从正整数扩展为正实数,能够有效地提高灰色模型的预测精度[8]。在分数阶灰色模型中,分数阶反向累加灰色模型相对于传统的灰色模型具有预测扰动小、能够利用序列新信息等特点,受到许多学者关注[9]。因此本文根据电力价格的历史数据,以“历史数据拟合最好”作为目标函数,采用混合蛙跳算法求得最优阶数,结合分数阶反向累加灰色模型对电力价格进行预测,并对预测结果进行合理性分析。通过本文研究,以期为水电市场中电力价格的预测研究提供参考依据。
2 研究模型
2.1 分数阶反向累加GM(1,1)模型
分数阶反向累加GM(1,1)模型相对于传统的GM(1,1)模型具有预测扰动小、能够利用新信息的优点。根据分数阶反向累加灰色模型原理,r阶反向累加算子可写为[8]:
(1)
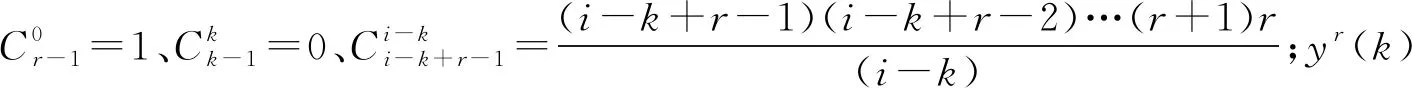
模型的时间响应式为:
(2)
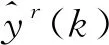
(3)



2.2 模型最优阶数确定方法
以历史数据拟合最优为目标函数,可挖掘历史数据的内在规律,为将来的预测奠定基础,具体见式(4)。
(4)
式中:f2(r)为模型对历史数据拟合的程度,约束见式(5)。
St 0 (5) 本文采用混合蛙跳算法求解最优阶数模型,具体介绍如下: 混合蛙跳算法与粒子群优化算法一样,具有参数少、概念简单、容易实现的优点[11],该算法的具体过程如下: 初始化种群K={K1,K2,…,KN},其中ki={r1,r2,…,rs}为第i只青蛙,也为优化问题的s维解。将每一个个体蛙代表的s维解带入目标函数,求得每个个体蛙对应的适应值,根据适应值对每个青蛙个体降序排列。对整个群体进行分组,具体分组方法参考文献[12]。 将种群个体划分好组别后,把每一个模因组内具有最好适应值和最差适应值的青蛙分别标记为Fb和Fw,而该种群中具有最优适应值的青蛙标记为Fg。然后,对模因组内的每一个青蛙执行局部位置更新操作,具体更新公式见式(6)-式(7): D=R(Fb-Fw) (6) Fw=Fw+D (7) 式中:R为0-1内的随机数,D为青蛙移动的距离,-Dmax 如果更新后得到的青蛙优于原来的青蛙,则可替代原模因组内的青蛙Fw;否则,用Fg代替Fb,执行局部位置更新操作,见式(8)-式(9): D=R(Fg-Fw) (8) Fw=Fw+D (9) 如果上述操作仍然不能获得更好适应值的青蛙或移动过程中超过了青蛙所允许的最大移动距离,那么就随机生成一个新的青蛙直接替代原来的Fw。重复数次以上局部位置更新操作,并将所有模因组内的青蛙重新混合排序和划分模因组,再执行下一轮的数次局部位置更新操作,直到满足预先设定的收敛条件或者达到混合最大迭代次数为止。 采用相对误差对模型的预测效果进行评价,相对误差公式见式(10): (k=n+1,n+2…m) (10) 其中,相对误差越小,模型越优。 我国长江中上游与珠江红水河两个地带特别适合开发水电站,这两个区域水能资源特别丰富,开发条件优越。而云南省正好位于这一地区,具有很好的水电开发前景,可开发水电站装机容量9 795×104kW,居全国第二[13]。 本次采用文献[5]中的水电电力价格作为基础数据。其中,2015年4月至2016年3月作为训练数据,2016年4月作为验证数据,具体数据见表1。 表1 水电电力价格 首先对表1数据进行一定的处理,具体处理过程见文献[14]。根据式(4)-式(5)结合2.1中的分数阶反向累加GM(1,1)模型,构造最优阶数模型,使用混合蛙跳算法对模型进行求解(种群大小为100,进化代数为100代),混合蛙跳收敛过程见图1。 图1 混合蛙跳算法收敛过程图 从图1可以看出,混合蛙跳算法具有较好的收敛能力,在第37代已经完全收敛。从图1也可以可以看出,最优阶数为0.027。 根据最优阶数,结合2.1中的分数阶反向累加GM(1,1)模型,对研究区水电市场中电力价格进行预测,预测结果见图2。 图2 分数阶反向累加GM(1,1)模型模拟与预测结果图 从图2可以看出,分数阶反向累加GM(1,1)模型具有较好的模拟和预测效果,模拟和预测的平均相对误差分别为5.070%和0.025%。 为了验证本文模型的合理性,将本文模型与人工神经网络模型、IGM(0,N)模型进行比较,各个模型的预测结果见表2。 表2 各个模型模拟与预测结果 从表2可以看出,本文的分数阶反向累加GM(1,1)模型具有最好的模拟效果和预测效果。本文模型相对于人工神经网络模型与IGM(0,N)模拟相对误差分别低14.378%和3.743%,本文模型以历史数据拟合最好作为目标函数,寻求模型阶数,这也是本文模型对训练数据模型效果好的原因。而本文模型相对于人工神经网络模型与IGM(0,N)预测相对误差分别低4.635%和6.015%,这是因为本文模型采用反向累加的方式构造模型,加大对新数据的利用,使模型能够充分利用新信息,能够有效地处理新旧信息不一致的问题[15]。而水电市场中的电力价格受多种因素影响,因此电力价格的历史数据常常会出现不一致的问题,而且本文模型的阶数为分数阶,也能提高模型的精度。同时,人工神经网络模型则容易陷入局部最优解,而影响模型的精度。IGM(0,N)属于统计模型,对数据依赖较大,而且不能利用新信息,因此精度也在一定程度上受到影响。 本文以云南省水电市场中的电力价格预测为例,使用混合蛙跳算法、分数阶反向累加GM(1,1)模型对云南省水电市场中的电力价格进行预测,最后得出本文模型的模拟和预测的相对误差分别为5.070%和0.025%。本文模型相对于人工神经网络模型与IGM(0,N)模拟相对误差分别低14.378%和3.743%;本文模型相对于人工神经网络模型与IGM(0,N)预测相对误差分别低4.635%和6.015%。 本文模型使用反向累加的方式构造模型,加大对新数据的利用,使模型能够充分利用新信息,能够有效地处理新旧信息不一致的问题,同时本文模型的阶数为分数阶,也能提高模型的精度。 综上可以得出,本文模型对于水电市场中的电力价格预测具有一定适用性。2.3 预测效果评价
3 实例计算与应用
3.1 模型计算
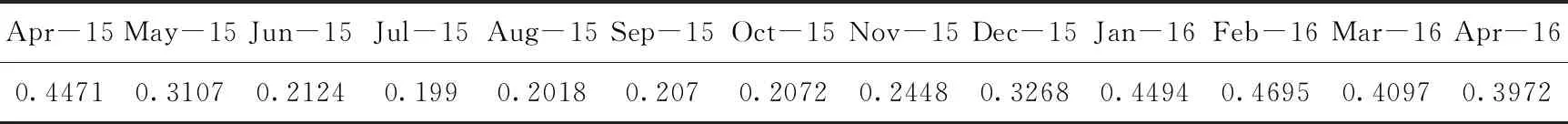


3.2 模型对比与验证

4 结 论
