小苹果不等式

张蕴禄

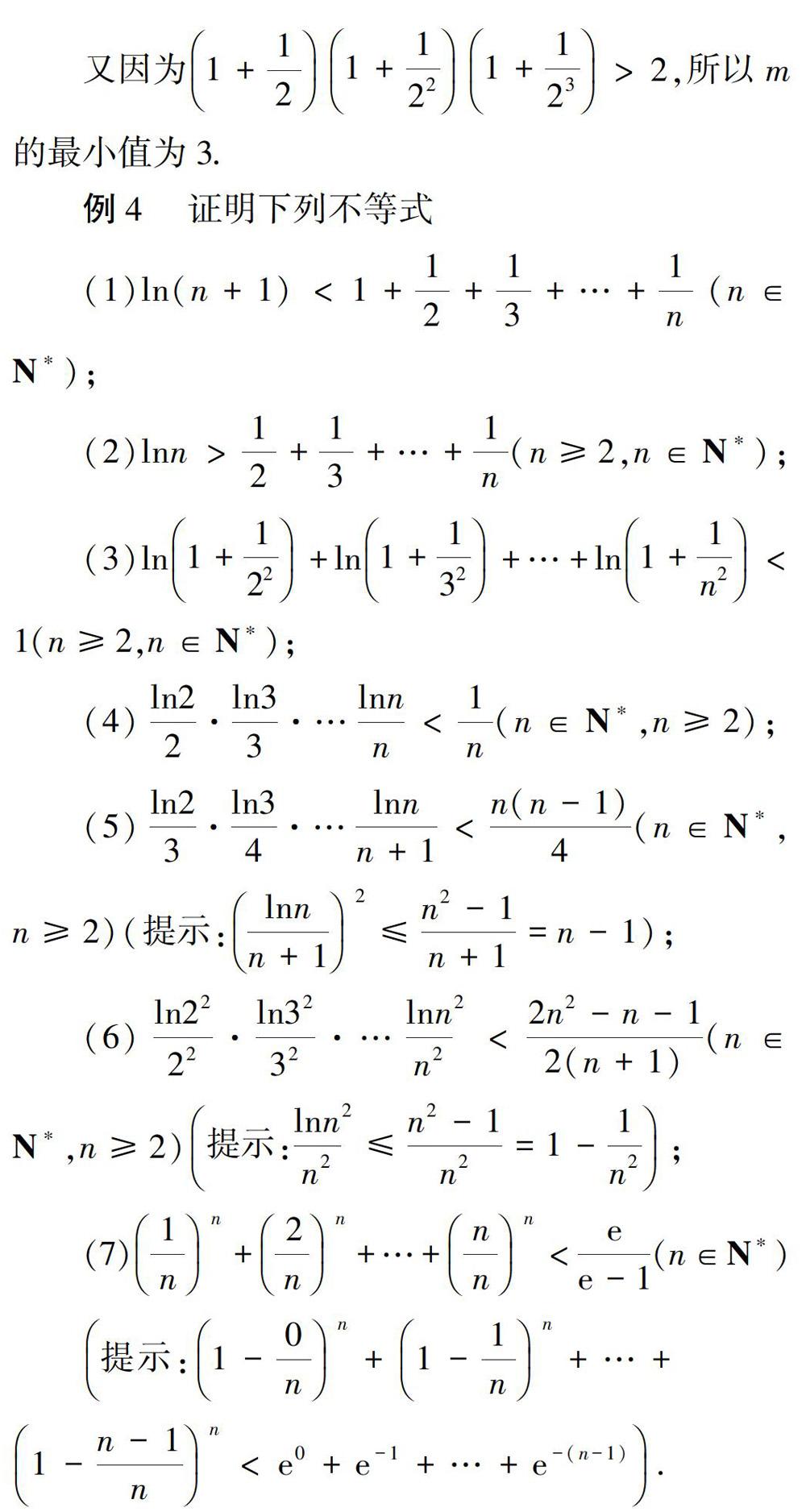
有句歌词：“你是我的小苹果，小呀小苹果，怎么爱你都不嫌多，……”。此文要说的是一个与函数与导数有关的常用不等式，堪称不等式中的“小苹果”。所以这里笔者亲切地称作为“小苹果不等式”。

小苹果不等式：

（1）ln（1+x）≤x，当且仅当X=0时取等号;

（2）e^x≥x+1，当且仅当x=0时取等号。

由于此不等式属于常见不等式。其证明过程大家也非常熟悉（限于篇幅，证明过程略）。事实上两组不等式是等价的。不等式（2）是（1）的指数形式;不等式（1）是（2）的对数形式。

1 赋值功能的神奇

小苹果不等式的赋值功能非常强大，如果对小苹果不等式及其各种变形中的x进行不同的赋值，可使许多看似棘手的不等式问题得到解決。

例4中的不等式都是从某些函数与导数综合题或高考题中截取的。大家可以从中领略小苹果不等式赋值功能的强大和神奇。

2 式子变形的密码

函数与导数的综合问题在历年高考和各类模拟试题中一般处于压轴题的位置。作为压轴题得分一般都很低。因为有时在推理和运算过程中需要对表达式进行适当的变形与调整，而在很大程度上，这个变形与调整往往是整个题目能否解决的一道分水岭，甚至成为很多学生不可逾越的鸿沟。其实很多表达式的变形与调整与小苹果不等式有关。只要我们的学生心里装着小苹果不等式，对小苹果不等式及其衍生的一些常用函数的组合有较高的敏感度，那么就会使十分困难的表达式的变形与调整变成一件十分自然和水到渠成的事情了。

3 不等式放缩的利刃

函数与导数的综合问题离不开不等关系。离不开成立问题。无论是不等关系还是恒成立问题，尽管都与函数的单调性有关系，但是在很多情况下需要对不等式进行适当的放缩来完成。在很大程度上，这种不等式的放缩与小苹果不等式不无关系

不等式的放缩，小苹果不等式是一把利刃，如果没有它的参与不知要多走多少弯路。

4 高考命题人员的最爱

上文中的诸多实例几乎全部来自于全国各地的高考试题，这已经充分说明小苹果不等式是广受高考命题人员青睐的。不仅如此，在历年高考试题中许多函数与导数题目就是直接以小苹果不等式为函数模型进行命制的。

众多的高考试题都以小苹果不等式为切入点，难免有重复和雷同之嫌。出现这种情况的一个重要原因除了小苹果不等式的重要性之外。还有一个重要原因就是小苹果不等式在高考试题的编拟过程中是很难绕过去的。众所周知。高中数学分别涉及到了幂函数、指数函数、对数函数以及三角函数的导数。那么高考试题中由指数函数、对数函数以及相关组合为函数模型就司空见惯了。而小苹果不等式正是指数函数、对数函数（或平移、组合后），以及切线等内在关系的一种体现，所以很多题目都或多或少有它的影子，进而成为命题人员的最爱也就不足为怪了。