数学核心素养的高考测评及其培养

陆吉健 丁姣娜

[摘要]本文选取2017-2019这三年的浙江省高考数学试题作为研究样本，建构出高考中数学核心素养测评的编码分析框架，量化编码后发现，逻辑推理和直观想象是2019年高考数学测评中有明显增多的数学核心素养。最后。也提出了对日常高中数学教学中培养数学核心素养的启示。

[关键词]数学核心素养;高考测评;逻辑推理;直观想象;浙江高考

1 研究背景和问题

数学学科核心素养是数学教育育人价值的核心体现，是数学课程目标的集中体现在学习数学和应用数学的过程中，学生需要发展数学学科的核心素养。《普通高中数学课程标准（2017年版）》（以下简称《标准》），提出了六个数学核心素养：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析这六个方面。在高考试题中，核心素养与四基、四能融为一体，往往是高考试题背后的考查核心。而且，在每一题背后，往往同时考查了多个数学核心素养。

那么，该用怎样的分析框架，来进行高考中数学核心素养测评的编码分析？近年来的高考数学试题测评数学核心素养的情况，又是如何的？日常高中数学教学中，又该怎样进行数学核心素养的培养？基于这些问题，利用内容分析法及团队已有习题编码分析操作，选取2017-2019这三年的浙江省高考数学试题作为研究样本，在深入编码分析后，提炼出高考中数学核心素养测评的编码分析框架，并量化呈现出了这三年的的高考数学试题测评数学核心素养的情况，也提出了对日常高中数学教学中培养数学核心素养的启示。

2 高考中数学核心素养测评的编码分析框架

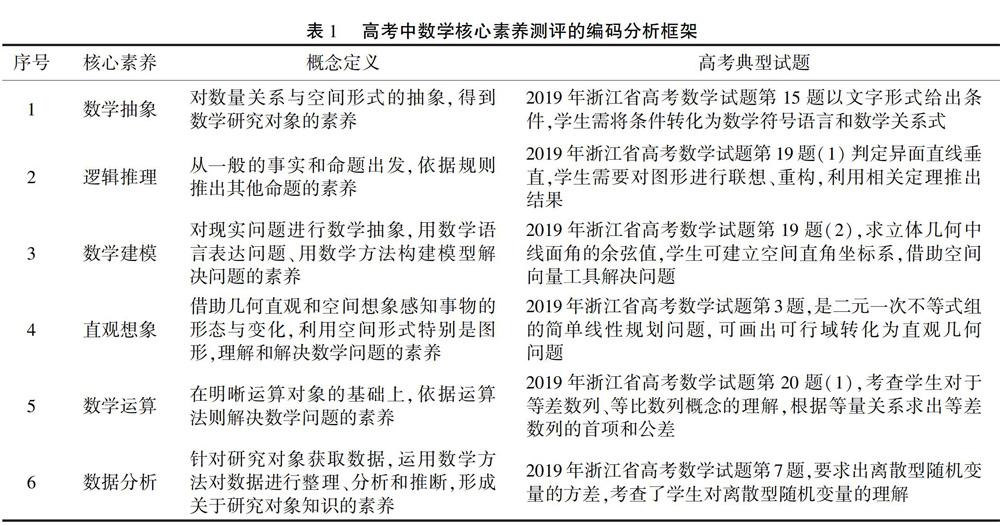
高考中数学核心素养测评的编码分析框架。主要是基于6个数学核心素养及其概念界定，配以2019年典型的浙江省高考数学试题，具体如表1所示。

其中，数学抽象主要包括从数量与数量关系、图形与图形关系中抽象出数学概念以及概念之间的关系，从具体的背景中抽象出一般规律和结构，并运用数学语言予以表征。逻辑推理主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比;一类是从一般到特殊的推理。推理形式主要有演绎。数学建模过程主要包括：在实际情境中从数学的角度发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题直观想象主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律;建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路。数学运算主要包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等。数据分析过程主要包括：收集数据，整理数据，提取信息，构建模型，进行推断，获得结论。

3 高考中数学核心素养的测评情况

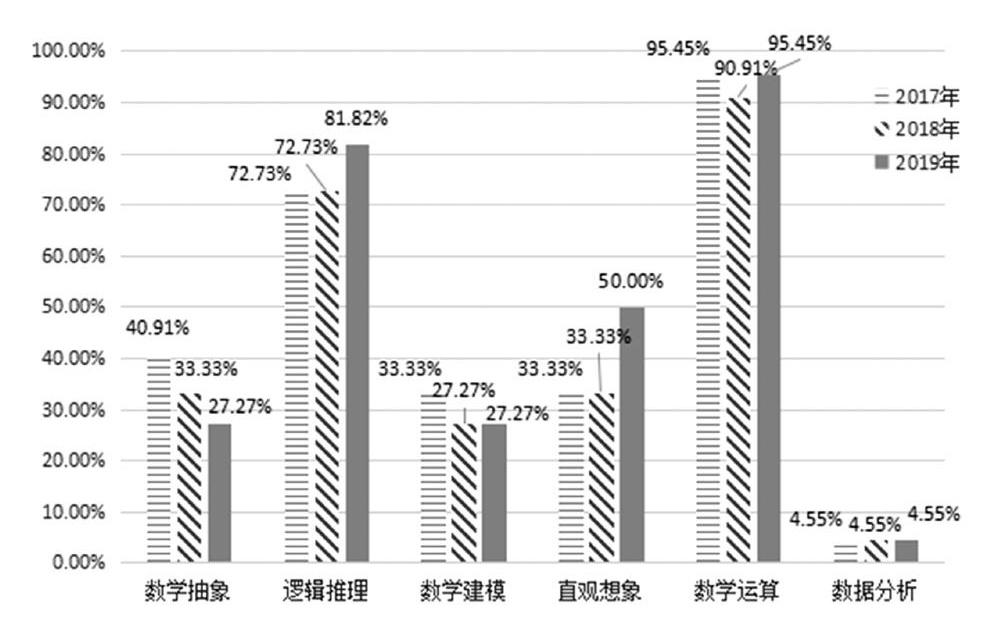
基于高考中数学核心素养测评的编码分析框架，对2017年到2019年的浙江省数学高考试题，进行数学核心素养测评情况编码分析后，发现：（1）数学运算和逻辑推理，是高考数学主要测评的数学核心素养;（2）数学抽象、数学建模和数据分析，则是高考数学测评较少的数学核心素养;（3）逻辑推理和直观想象，是2019年高考数学测评中有明显增多的数学核心素养。具体情况如图l所示。

具体而言，2017至2019年浙江高考中数学核心素养的测评比例，总体相差不大。其均值，由高到低依次为：数学运算（93.9%）、逻辑推理（75.8%）、直观想象（38.9%）、数学抽象（33.8%）、数学建模（29.3%）、数据分析（4.5%）。从中可以明显看出，数学运算和逻辑推理的测评比例均值都超过了四分之三，即75%，是高考数学主要测评的数学核心素养。毕竟，数学运算和逻辑推理是高中生及其未来学习、工作和生活中数学应用的主要技能。另外。数学抽象、数学建模和数据分析的测评比例均值都低于40%，是高考数学较少测评的数学核心素养，尤其是数据分析核心素养，该核心素养的测评比例均值甚至低于5%。

与此同时，相对于2017年和2018年而言，2019年的浙江高考中数学核心素养的测评中，逻辑推理和直观想象的测评比例分别有明显增多，分别增多到了50.0%和81.8%。相对于2017年和2018年的33.3%和72.7%均值，增多了约50.0%和12.5%，尤其是逻辑推理。毕竟，人工智能等技术的发展，逻辑推理和直观想象能力的作用越来越重要，尤其是逻辑推理能力。

4 指向高考的数学核心素养培养

通过对2017-2019年数学核心素养高考测评情况的编码分析，进一步概括提炼出如下指向高考的数学核心素养培养启示。

4.1 增强对逻辑推理和直观想象核心素养的要求和实践

数学高考对于学生思维的灵活性有很高的要求，具体体现在对逻辑推理、直观想象等核心素养的考查上。这就要求学生在把握数学概念本质基础上构建知识点之间的关联，包括异同点、递进关系等。具体可以通过变式教学的方式，来帮助学生掌握概念本质，辨析概念差异，以达到提升学生逻辑推理、直观想象核心素养的目的。

变式教学就是教师有目的、有计划地对命题进行合理的转化。教师可以变更命题中非本质的特征，变换命题的条件和结论、内容和形式、配置实际应用的各种环境等，从而引导学生对命題进行不同角度、不同层次的探究。

首先教师可以引导学生探究同一问题的一题多解，从多种解法中归纳数学本质。总结提炼数学思想。对于空间几何问题，在一题多解的过程当中，深化了学生对于几何体的空间理解。提升学生的直观想象能力：教师也可以改变命题条件和结论，深刻把握数学问题的本质，为学生构建知识体系奠定基础，也培养到了学生的数学抽象的核心素养：教师也可以让学生参与到编题、讨论交流心得的过程中，在创新合作、交流总结的过程中进一步深刻把握知识的核心，培养学生的创新精神。

更进一步，教师在变式教学中，注重发挥学生的主体作用，关注知识点间的关联性。教师设计有针对性的问题引导学生充分参与课堂中，体会知识间的关系，提出有价值的问题。学生灵活运用所学知识，根据自己的理解形成知识结构，有助于培养逻辑推理能力。例如在2019年浙江省高考数学试题的第20题第（2）小题中，

4.2 保持对数学运算核心素养的实践和严谨性要求

保持数学运算在课堂中的实践和严谨性。是目前高三学生必要的内容。通俗的讲，教师要本着“宁可少讲一道例题，也要留更多的时间给学生运算”的态度。

数学运算核心素养的培养在浙江省数学高考中考查频率居首位，教师需要更多关注学生运算的正确率、算理的理解和运算过程的严谨性。

在高三复习课中。很多时候教师在有限的课堂时间中只是引导学生理顺解题思路，总结解题方法，而把运算留给学生在课后完成，只要答案正确即可。弱化了算法、算理、运算技巧的指导，人为将运算训练与思维训练割离开来。事实上，在运算过程中，往往包含着学生对于概念、算理和运算法则的理解。

留一定时间给学生去做运算操作，首先在于解决运算技能较弱的问题。让学生经历整个运算过程，体会运算中的难点、易错点。教师可根据学生暴露出的问题有的放矢的进行指点，可以是运算技巧的点拨，可以是易错点提醒、指导，亦或是运算方向上的选择。其次在于解决知识掌握不清的问题。发现学生在运算过程中概念理解不透彻、公式性质记忆不准确的问题，从而进一步制定复习计划。例如学生对于“两角和与差的三角函数”公式识记不清导致运算出错，属于概念理解不清导致公式识记混淆的问题，则需要教师带领学生对“两角和与差的三角函数”公式进行推理和证明。在理解算理的基础上识记公式。能达到事半功倍的效果。与此同时，不仅仅培养了学生数学运算的核心素养，在逻辑推理、数学抽象方面也相应获得提高。

4.3 留意对数学抽象、数学建模和数据分析核心素养的培养

《标准》指出，数学课程的目标在于让学生能用数学的眼光去分析世界。数学抽象、数学建模以及数据分析是学生在新时代分析各种现象的关键素养。

数学抽象贯穿于整个数学的产生、发展与应用过程。众所周知，学生的数学学习过程是一个自主构建对数学知识理解的过程。他们带着自己的知识背景和活动经验理解数学。前面已经提到。变式教学在改变概念非本质条件时能凸显概念的本质条件，便于学生理解概念，进行有效的数学抽象活动。此外教师在高三学生的复习课中，要充分考虑学生理解水平和认知风格的差异，采用多样化的教学策略，帮助学生更好地理解数学知识。

虽在高考中对于数学建模、数据分析要求较低，但是在信息社会对数据分析、处理能力和数学建模解决问题提出了更高的要求。在高三复习阶段以及整个高中阶段，教师都要注重设计实际场景，引导学生运用所学数学知识解决问题，多設计数学实践活动，在实践活动中提升解决现实问题的能力。

4.4 注重对学生探究精神、意志力与自信心的历练

在数学课堂中，教师应致力于“让探究活动成为课堂的常态”，应该充分发挥学生的主观能动性，让学生成为课堂的主体，探究数学问题，让学生的探究代替教师的讲授。这不仅仅是高三学生需要的。更是所有阶段学生所需要的。

首先，学生每天的数学学习，都是一个不断积累、优化、迁移、螺旋上升的过程。高三的复习不能仅仅是单纯回顾旧知。而更应该是构建知识点之间关联的重要阶段。设计合理数学问题，引导学生探究问题并总结规律能帮助学生构建知识体系，培养数学核心素养。其次，在高考中出现的题往往比较新颖、复杂，学生很难在第一时间形成完整的解题思路这是对学生心理的考验。许多考生受考场紧张情绪的影响，出现畏难心理，容易出错。倘若在平时的教学过程中，学生乐于探究，享受探究合作、寻求答案的快乐，那么学生的数学学习兴趣也相应提升了。面对考试中的问题，学生会抱着一种积极、意志坚定的态度去面对，能有效提升学生的考试信心，有助于学生在考试中更好的发挥出自己的水平。