蒙特卡罗法液压缸动态特征可靠性灵敏度分析
2020-07-31陈鹏霏于泰龙贺宇新
*陈鹏霏,于泰龙,和 鹏,贺宇新
(1. 长春工业大学机电工程学院,吉林,长春 130012; 2. 长春职业技术学院机电学院,吉林,长春 130033)
0 引言
目前,随着液压缸驱动控制装置向高精度方向发展,对其动力学特性要求也越来越高[1]。同时,由于工程结构的复杂性,其模型求解通常具有隐式和非线性特征。如何准确、高效地求解隐式、非线性结构的可靠性,一直是可靠性分析领域的研究热点之一[2]。
本文通过揭示引起液压缸爬行现象(即自激振动现象)的本质原因及其作用机理,采用蒙特卡罗法可靠性分析理论,对液压缸动态特征参数进行可靠性灵敏度分析研究。
1 液压缸动态特征分析
1.1 动力学模型的建立
液压缸属于液压系统中的执行元件,可将油液压力能转换为机械能输出。虽然液压缸的种类繁多,但其工作原理基本相同。单活塞杆双作用式液压缸的工作原理简图,如图1 所示。
根据牛顿第二定律,其动力学方程可表示为

式中:m为活塞和负载的等效质量;cF为介质粘性阻尼力;fF为运动过程中的摩擦力;tF为液压弹性力;LF为外加负载。

图1 单活塞杆液压缸的工作原理图 Fig. 1 Schematic diagram of hydraulic cylinder about single piston rod
由文献[3]可知,当活塞低速运动时,液压弹簧刚度具有非线性特征,而摩擦力具有时变性特征。因此,液压缸驱动装置可抽象为如图2 所示的模型。
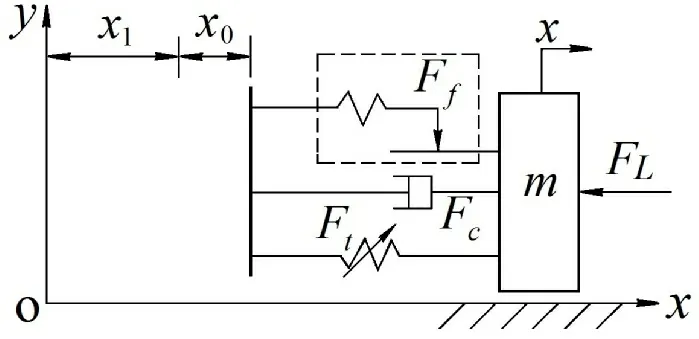
图2 液压缸活塞的非线性动力学模型 Fig. 2 Nonlinear dynamic model of hydraulic cylinder piston



1.2 非齐次线性微分方程的求解

由式(6)可知,液压缸活塞低速时呈现出明显的非线性运动特性。此时,活塞的运动状态将随预期运动速度v的不同,分别处于边界润滑区域、混合润滑区域和流体动压润滑区域三种情况。其对应的速度时域图像,分别如图3 中的分图(a)、(b)、(c)所示。
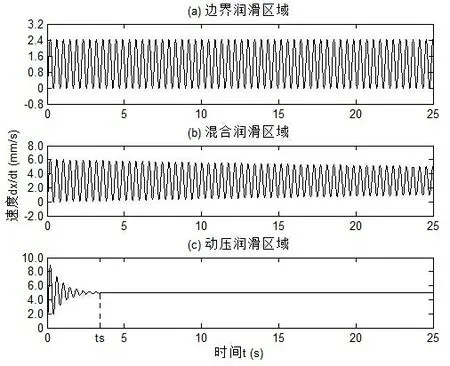
图3 不同润滑状态下的速度时域图像 Fig. 3 Sketch map of velocity-time domain under different lubrication conditions
如图3(a)所示,当液压缸处于边界润滑区域时,活塞运动体现出负阻尼特性,即随着活塞瞬时速度增大,摩擦力会减小,导致阻尼比为负值( 0<ξ)。因此,活塞在整个运动行程内均出现液压爬行现象(即自激振动现象)。如图3(b)所示,当液压缸处于混合润滑区域时,活塞运动的负阻尼特性减弱,导致阻尼比较小(ξ→0)。因此,活塞在整个行程内会出现时缓时急的液压爬行现象。但是,随着运动时间的增加,瞬时速度d /dx t的变化幅度会越来越小。如图3(c)所示,当液压缸处于流体动压润滑时,活塞运动体现出正阻尼特性,即随着活塞瞬时速度的增大,摩擦力将增大,阻尼比为正值( 0>ξ)。于是,活塞仅在整个行程的初始处,出现了短暂的液压爬行现象,随即便迅速衰减为等速运动。
综上所述,液压爬行现象(即自激振动现象)的产生,是造成液压缸低速运动失效的主要原因。然而。机床设备中使用的液压缸驱动装置,由于受到工件材料、技术要求、环境温度和维修周期等因素的影响,导致活塞预期运动速度、油液粘度和体积弹性模量等参数不断变化,会严重影响动态系统的阻尼和刚度特性。从而,使低速运行中的液压缸活塞在不同的润滑区域间变换,极易产生自激振动现象(或爬行现象),导致液压缸的运动状态发生失效,降低机床的加工精度可靠性。因此,考虑到各种随机因素的影响,构建液压缸运动系统可靠性模型,求解各种影响因素的可靠性灵敏度,对提高运行中液压缸的动态可靠性,具有积极作用。
2 蒙特卡罗法可靠性灵敏度分析
2.1 Monte Carlo 法分析失效概率
蒙特卡罗法(Monte Carlo 法,简称MC 法)作为可靠性分析随机模拟法中的一种基本方法,其基本思想是将数值积分问题转化为具有同样解答的概率问题,采用数字模拟的方式来进行求解计算。

因此,只要N足够大,失效概率fP可由结构的失效次数占总的抽样次数N的频率来表示。
2.2 可靠性灵敏度求解

3 液压缸低速运动可靠性分析
机床在加工工件时,为保证表面粗糙度和加工精度,一般要求低速进给切削。由图3 可知,对于液压进给系统而言,当活塞运动处于边界润滑区域,或者混合润滑区域时,液压缸均会出现较明显的爬行现象(即自激振动现象),很难保证加工质量。只有当活塞处于流体动压润滑区域,且瞬时运动速度x˙的调整时间ts足够小时,才能保证液压缸进给驱动装置的加工可靠性。
已知某机床的液压进给驱动系统,采用的是进油节流且回油有背压的回路。若缸筒内径为100 mm,活塞杆直径为50 mm,总有效行程为150 mm;活塞负载的总质量为370 kg;油液密度为900 kg/m3;液压缸的预期驱动速度为3 mm/s。

显然,式(14)中的ts属于隐式参数,不能通过显式解析式进行表达。但是,ts可以先根据式(6) 通过数值方法进行求解。之后,采用Monte Carlo 法对式(14)进行可靠性灵敏度分析。经分析计算后的结果,如表1 所示。

表1 液压缸低速运动可靠性灵敏度分析结果 Table 1 List of results about reliability sensitivity analysis under low speed motion on hydraulic cylinder
由表1 中的数据可知,液压缸阻尼系数c0无论是均值灵敏度Sc0,还是标准差灵敏度Sσc0,均明显大于液压弹簧刚度k的均值灵敏度Sk和标准差灵敏度Sσk,说明相对液压弹簧刚度来说,系统阻尼对液压缸动态可靠性的影响,更加显著。同时,表1 中数据显示,阻尼系数c0和液压弹簧刚度k的均值灵敏度Sc0、Sk均为负值,说明增加阻尼和提高液压弹簧刚度均有利于减小活塞运动的失效概率;而其标准差灵敏度Sσc0和Sσk为正值,说明工作中阻尼和液压弹簧刚度随机变化的偏差较大,均会提高活塞运动的失效概率。
4 结论
1) 与液压弹簧刚度相比,液压缸驱动系统的阻尼系数对活塞低速运动可靠性具有更大的影响。因此,控制好活塞表面的润滑状态,对保证活塞的运动可靠性,意义重大。
2) 采用Monte Carlo 法对于隐式结构的可靠度求解,具有良好的适用性,且对于强非线性问题也很有效。然而,Monte Carlo 法的计算精度是建立在大量抽样结果基础上,因此对于大型复杂结构的可靠性分析,其计算效率不易被接受。
