模型不确定下船舶动力定位鲁棒控制器设计*

朱梦飞 徐海祥 余文曌 卢林枫

(武汉理工大学高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063)

0 引 言

随着海洋资源开发的深入与先进船舶技术的不断发展，船舶动力定位控制技术广泛应用于各类工程作业船、科学考察船和海洋平台等，已成为深海资源开发不可或缺的关键支持技术，在海洋资源勘探、航行补给等领域应用甚广[1-2].在海洋中作业的船舶会受到未知时变的环境扰动，如风、浪、流等；同时，复杂多变的海况将导致船舶模型参数产生不确定扰动.对于动力定位系统，这些不可忽略的动态未知扰动不仅会影响定位精度，还会使控制输出不稳定，从而导致推进器磨损以及能耗增加.

文献[3]提出了一种环境最优位置控制(WOPC)方法，该方法根据环境扰动的大小调整艏向角以减少能量消耗.文献[4]针对外部扰动为已知常值和未知常值的情况，设计了鲁棒无源输出反馈控制器，实现船舶定位控制的渐近稳定.针对在未知环境力作用下船舶横向和艏向所受到的力和力矩具有不便测量的特点，文献[5]提出一种基于非线性分离式原理的动力定位环境最优控制律.文献[6]提出了一种基于Backstepping的船舶动力定位正交神经网络自适应控制方法，同时考虑非线性模型和未知常值环境扰动，采用正交神经网络对数学模型的非线性项进行逼近，并采用自适应积分估计环境扰动.上述文献大多考虑的扰动为常值，并不满足实际情况下扰动连续非线性变化的特征.文献[7]设计了一种滑模控制方法，基于1∶150比例的模型船实验证实了其有效性.针对具有不确定性和未知时变扰动的水面船舶动力定位问题，文献[8]应用矢量反步法设计了一种鲁棒自适应神经控制器，采用径向基函数(RBF)神经网络对船舶模型动力学不确定性和时变扰动进行补偿.考虑未建模环境扰动，文献[9]提出了一种基于无源滤波的反步逆最优控制器，利用Lyapunov函数设计了未建模扰动环境力自适应律和渐进稳定的控制律，同时满足了局部性能指标和全局性能指标.文献[10]采用鲁棒自适应技术和反步法设计了一种船舶艏向容错控制器，处理外部时变环境扰动和艏向传感器突发故障，设计参数自适应律来估计鲁棒项的上界，仿真结果验证了控制器的有效性.针对具有未知模型参数和未知时变扰动的船舶动力定位问题，文献[11]通过将参数不确定的船舶运动数学模型和未知时变扰动分别表示为参数形式，构造处理扰动的观测器，并利用自适应矢量反步法，设计了动力定位鲁棒自适应控制律.

在分析相关文献的基础上，针对船舶动力定位控制问题，同时考虑船舶模型参数不确定性和未知时变环境扰动，为简化设计过程，假设扰动上界已知，本文提出了一种船舶动力定位鲁棒控制方法.基于一艘平台供应船模型的对比仿真结果验证了本文所提出控制律的有效性和优越性.

1 问题的描述

1.1 船舶数学模型

对于低速运动的船舶，考虑纵荡、横荡、艏摇三个自由度方向上的平面运动，根据运动学和动力学理论，船舶的非线性数学模型为

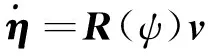
(1)

(2)

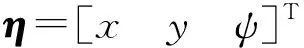
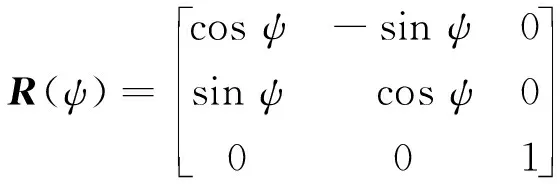
(3)

且满足R-1(ψ)=RT(ψ)和‖R(ψ)‖=1，‖·‖表示向量或矩阵的2范数；M∈R3×3为惯性矩阵，D∈R3×3为线性阻尼矩阵，且M是正定的；b为风、浪、流等环境扰动，其未知但有界；d为船舶模型参数不确定项.

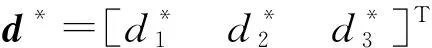
1.2 切比雪夫正交神经网络

切比雪夫正交神经网络广泛应用于控制工程中，具有很强的连续非线性函数逼近能力和较快的收敛速度.其模型可以定义为

(4)

式中：wj(j=1,2,…,n)为隐藏层和输出层之间的权重;Φj={Φ1(X),Φ2(X),…,Φn(X)}为一组切比雪夫正交多项式.

(5)

在假设1和假设2下，设计船舶鲁棒自适应控制律，在存在动态扰动的情况下，使得船舶的位置收敛到期望的位置，同时保证闭环控制系统中所有的信号一致最终有界.

2 动力定位鲁棒控制器设计

在假设1和假设2下，结合动态面控制技术，设计具有动态扰动的鲁棒控制律，使得船舶的位置和艏向收敛到期望的位置和艏向，实现船舶的动力定位控制.控制器设计包括以下两个步骤.

步骤1定义船舶的位置误差向量为

z1=η-ηd

(6)

对式(6)求导可得

(7)

选取虚拟函数向量α

α=-R-1(ψ)K1z1

(8)

式中：K1为正定对称设计矩阵.

引入状态向量Xd，对虚拟函数向量α设计一阶低通滤波器，其表示为

(9)

式中：Td为滤波器时间常数.

步骤2定义船舶的速度误差向量为

z2=v-Xd

(10)

对式(10)求导，并乘上惯性矩阵M可得：

(11)

记神经网络逼近误差和模型参数不确定项所构成的复合扰动ε的界为

ε*=δ*+d*

(12)

采用正交神经网络估计时变环境扰动项RT(ψ)b，则设计的控制律为

(13)

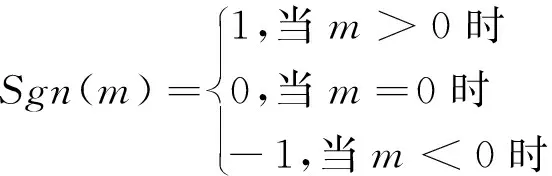
(14)

定义系统边界层误差向量为

z3=Xd-α

(15)

构造如下Lyapunov函数.

(16)

对其求导可得：

(17)

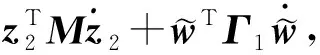
(19)

设计神经网络权值自适应律为

(20)

式中：Γ1为待设计矩阵.

(21)

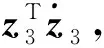
(22)

(23)

根据上述各式，可得：

(24)

式中：λmin(·)为矩阵的最小特征值，并且

(25)

(26)

λmin(K1)-β1-β2>0

(27)

(28)

(29)

根据上述分析，可得以下定理.

定理1对于具有模型参数不确定性和时变环境扰动的系统(1)和(2)，设计出具有一阶低通滤波器的已知扰动界鲁棒控制律，通过合理设计参数矩阵K1、K2，以及滤波器时间常数Td，能够使得船舶的位置收敛到期望位置上，并保证该闭环系统中所有信号一致最终有界.

证明解式(24),可得

(30)

因此V(t)是一致最终有界的.根据式(16)可知，z1、z2和z3一致最终有界，那么该闭环系统中的所有信号均一致最终有界，定理1得证.

3 仿真结果与分析

表1 船舶模型参数

本文以两种情况对平台供应船进行仿真研究.

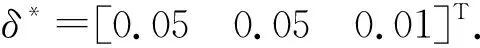
(31)

式中:Δ1为补偿神经网络逼近误差的鲁棒项；ε1=δ，表示神经网络逼近误差.

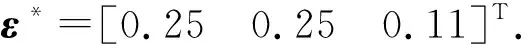
(32)

式中:Δ2为补偿模型参数不确定项和神经网络逼近误差的鲁棒项；ε2=ε.

两种情况下的参数设置相同，相关设计参数矩阵定义为

选取的神经网络初始权值矩阵为

并通过权值自适应律进行权值在线更新，以估计环境扰动.

仿真结果见图1～5，其中τ1为情况1下的控制律，τ2为情况2下本文设计的鲁棒控制律.北东坐标系下的船舶定位轨迹见图1，表明τ1和τ2能够使船舶到达期望位置并长时间保持其位置.在τ1和τ2的作用下船舶位置见图2，τ1作用下船舶位置存在一定的误差且艏摇角存在超调；τ2能够使船舶准确保持在期望位置，具有较强的鲁棒性.船舶速度见图3，表明τ1和τ2作用下的u，v和r是有界的，且τ2作用下的速度更为平滑.环境扰动的估计见图4，τ1，τ2均能够准确地估计时变环境扰动.图5为τ1和τ2作用下的控制输出是合理并且有界的，且τ2作用下控制输出更为平稳.上述结果表明，本文设计的鲁棒控制律在同时存在模型参数不确定性和未知环境扰动的情况下达到了满意的定点定位控制效果，与未考虑模型参数不确定性的情况相比，考虑了模型参数不确定性后，定位精度更高，控制输出更平稳合理，能够减少推进器的磨损，从而一定程度上降低能耗.

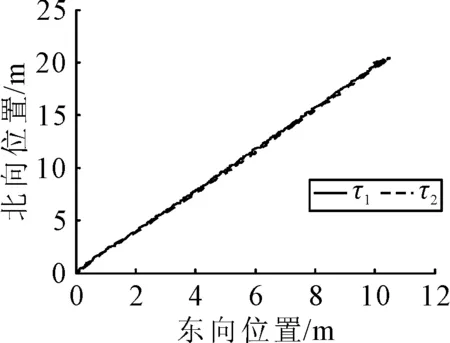
图1 北东坐标下船舶定位轨迹

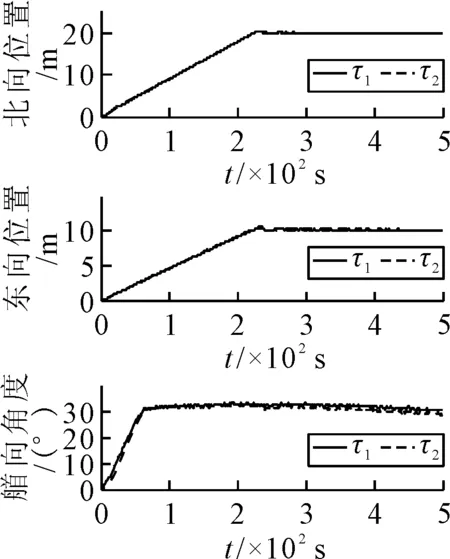
图2 船舶位置

图3 船舶速度

图4 环境扰动估计

图5 控制输出

4 结 束 语

同时考虑模型参数不确定性和时变环境扰动，本文设计了一种船舶动力定位鲁棒控制律.与动态面控制技术结合，利用一阶滤波器的微分项代替虚拟控制向量的微分项，使控制律设计过程中的微分运算用简单的代数运算代替，这样简化计算，易于在工程中实现.采用正交神经网络估计环境扰动，其具有很强的连续函数逼近能力且收敛速度较快.通过设计鲁棒项来补偿模型参数不确定项和神经网络逼近误差，并假设扰动上界已知以简化设计过程.应用Lyapunov函数证明了所设计的鲁棒控制律的稳定性，能够使船舶位置收敛到期望位置并保证该闭环系统的所有信号一致最终有界.最后对平台供应船模型进行了仿真，验证了本文所提出控制律的有效性.