典型双曲度板材冲压成形回弹差异分析*

赵 涵 胡 勇 蔡一杰 黄朝炎

(武汉理工大学教育部船舶技术高性能重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063)

0 引 言

船体曲面外板的成形按加工方式可分为热加工成形和冷加工成形.多年来，国内外船厂对双曲度外板加工一直是采用人工操作压力机与水火弯板相结合的方式进行的.板材的多点成形技术是目前解决上述问题较好的途径.多点成形是指由一系列规则排列、高度可调的基本体形成离散曲面代替传统模具进行三维曲面成形的板材柔性加工技术.李明哲等[1]对多点冲压成形的基本理论与实用技术进行了系统研究，并研制出了多点冲压成形样机.为了解决造船过程中船板在多点成形中的压痕问题，王呈方等[2-4]在分析研究相关成果的基础上，提出了使用“方形压头可调活络模具板材曲面成形装置”的三维曲面船体外板自动成形加工的技术，并基于该技术成功制造了“船舶三维数控弯板机”，该设备已运用在实际的船体外板加工生产中，但对于回弹的问题尚未得到有效的解决.

双曲度板材的冷冲压成形是一种大应变弹塑性变形，涉及材料非线性、几何非线性、边界条件的非线性，而其中影响成形精度的主要缺陷就是回弹，板材回弹与材料、厚度、目标曲面形状、接触摩擦等因素相关.Johnson等[5-6]对在固定模具冲压下的双曲度板材成形回弹问题进行了理论分析和实验验证，用回弹比的概念描述双曲度板材回弹的大小，推导出了在双向纯弯曲理论下的多个回弹比公式，为双曲度板的成形回弹研究领域奠定了理论基础.Xue等[7-8]将圆形板的成形过程中的应变分解为径向应变和轴向应变进行分析，通过旋转壳理论、板的纯弯曲理论和能量法对考虑了膜力作用和弯矩作用的圆形板的球模冲压回弹进行了分析，并计算出了圆形板的径向和周向回弹应变，预测了圆形板的回弹大小，进而将该理论推广至双向曲率相等的方形板和双向曲率不相等的圆形板，对比了其理论预测结果和实验结果，验证了其回弹计算的有效性，但其提出的方法无法完全适用于离散模具成形的问题.

随着有限元方法和计算机强大计算能力的结合，通过对板材进行网格划分，对非线性问题进行数值求解，使之能够满足工程实际要求，成为回弹补偿问题中常见的做法.李明哲等[9]通过板材回弹后的板材得出其与目标板面之间的变形量来计算出调整值来控制基本体冲头矩阵，从而对板材最终成形形状面进行反复修正，直到板材成形精度达到实际应用的要求，但是这种反复成形法对各种形状各种规格的板材成形的泛用性并没有得到讨论.张海明等[10]提出回弹修正算法，并用有理B样条曲面生成重构曲面，从而做到对板材成形的精度控制，可是文中并未对迭代修正过程中整体算法的收敛性进行研究，这限制了该种回弹补偿方法的推广使用.

为了解释双曲度板材的双向弯曲成形回弹问题，在通过离散模具时能对典型双曲度板材进行更好的回弹补偿.本文提出了双曲度板回弹大小的理论计算模型，表现了双曲度板回弹前后的几何变化的内在原因，得出了不同方向上板材的回弹区别，从而体现出双向回弹作用对回弹大小的影响.同时通过一系列的典型双曲度板的实验数据和相同条件下的有限元仿真数据，验证了双曲度板材成形回弹时双向回弹作用下的回弹大小差异问题和理论计算模型的正确性.

1 典型双曲度板回弹大小理论分析

1.1 回弹比

金属板材弯曲成形过程中，会经历弹性变形和塑性变形，当成形力卸载后，板材的曲率会在这个过程中减小，这就是回弹现象.板材的回弹可以通过一些物理量进行描述，比如回弹角、回弹曲率、回弹位移，以及回弹比等，其中回弹比被定义为回弹后与回弹前的曲率之比，即

(1)

式中：κf为回弹后板材的曲率；κ为回弹前板材的曲率.

单曲度板回弹前后的曲率易求得，故回弹比可以通过公式直接得出，但是双曲度板有着复杂的空间曲面，其回弹前后的曲率难以确定，故在应用回弹比公式时存在困难之处.对于板材成形而言需要的是准确的几何量，为了简化回弹描述和便于得出板材回弹的补偿值，结合船体外板的流线型方向主要是沿着船长和型深方向的特点，本文选用船体板的板长方向(x方向)和板宽方向(y方向)的曲率来描述其在相应方向上的曲面弯曲程度.由于船体板材的成形曲率半径通常大于加工板材的边长，故双曲度板材在某一方向上的曲率变化很小，因此板材在离散化之后的离散点处的所有曲率的均值可近似认为是双曲度在相应方向的弯曲曲率，同样双曲度板在该方向的回弹可以用回弹前后所有离散点的回弹比均值表示.

1.2 基本假设

在双曲度板材成形和回弹的整个过程中，板材的受力情况是非常复杂的，为了简化问题的求解，需要提出一些必要的假设.

1) 板材在冲压过程中的弹性变形忽略不计，塑性变形被认为是不可压缩的，即整个变形过程中体积不变.

3) 板材的横向剪应力忽略不计，且板材的厚向应变εz为小量，即εz≈0.

4) 板材的中性面始终保持在几何中面的位置不变.

5) 帆形板和马鞍形板的回弹差异是由于弯曲作用上的差异导致的，即仅考虑板材的弯曲效应.

1.3 帆形板与马鞍形板的回弹比差异分析

假设冲压双向曲率半径大小分别相同的帆形板和马鞍形板，即有

(2)

式中：ρ为双曲度板上某离散点的曲率半径；上标a为帆形板，上标b为马鞍形板；下标i为x,y两个方向，i=x,y.

基于假设1)，冲压过程中只发生了不可压缩的塑性变形，且认为板材成形过程中经历的是单一加载路径下的一次冲压，故加载期间应力与应变是一一对应关系，即可以使用形变理论，同时不需要考虑Bauschinger效应，因此存在如下关系.

(3)

式中：σi,εi分别为板材x,y方向上的应力和应变；σm为平均应力；等效应力σe、等效应变εe的定义为

(4)

考虑平均应力σm的定义，且根据假设1)板材变形过程中体积不发生改变，故σm=0，那么有两个方向的应力大小：

(5)

式中等效应力σe和等效应变εe之间的关系满足假设2)中的关系.基于假设5)，考虑到帆形板和马鞍形板受到弯曲应力，在x方向，两种形状板的受力情况相同，但在y方向，帆形板的上表面受压，下表面受拉，而马鞍形板则相反，即上表面受拉，下表面受压.

(6)

式中：z为到中性面的距离.基于假设5)，随着成形力卸载后，若卸载不引起反向屈服，则卸载过程相当于对板施加一个大小相同方向相反的弯矩所引起的弹性效应，且轴力的纯弹性效应将不改变曲率，则回弹后的曲率满足：

(7)

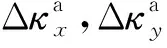
(8)

式中：E为板材弹性模量；μ为板材的泊松比.

而对于矩形截面板，同时基于假设5)，且卸载过程符合弹性关系时，加载弯矩Mi与对应方向上的最大应力(σi)max存在如下关系.

(9)

式中：h为指板材的厚度.将式(6)代入式(9)得：

(10)

将式(7)～式(10)代入式(1)中回弹比的定义中，可得出x,y方向的回弹比ηi.

(11)

(12)

2 双曲度板材冲压成形回弹实验和有限元仿真

2.1 双曲度板材回弹实验

本文对6组尺寸均为840 mm×840 mm×19.05 mm的Invar钢方形板进行了双曲度板材冲压实验，采用的冲压设备是某公司的SKWB-2000型船舶三维数控弯板机，见图1，其相关参数为：最大弯板厚度40 mm，压头尺寸100 mm×100 mm，上压头数量20×20，下压头数量21×21，单个压头压力20 kN，成形曲面为帆形、马鞍形.Invar钢的材料相关参数为：密度8 410 kg/m3,弹性模量123 GPa,泊松比0.25,屈服应力241 MPa,抗拉强度440 MPa,伸长率40%.板材的冲压形状是典型的帆形与马鞍形，见图2.

图1 SKWB-2000型船舶三维数控弯板机

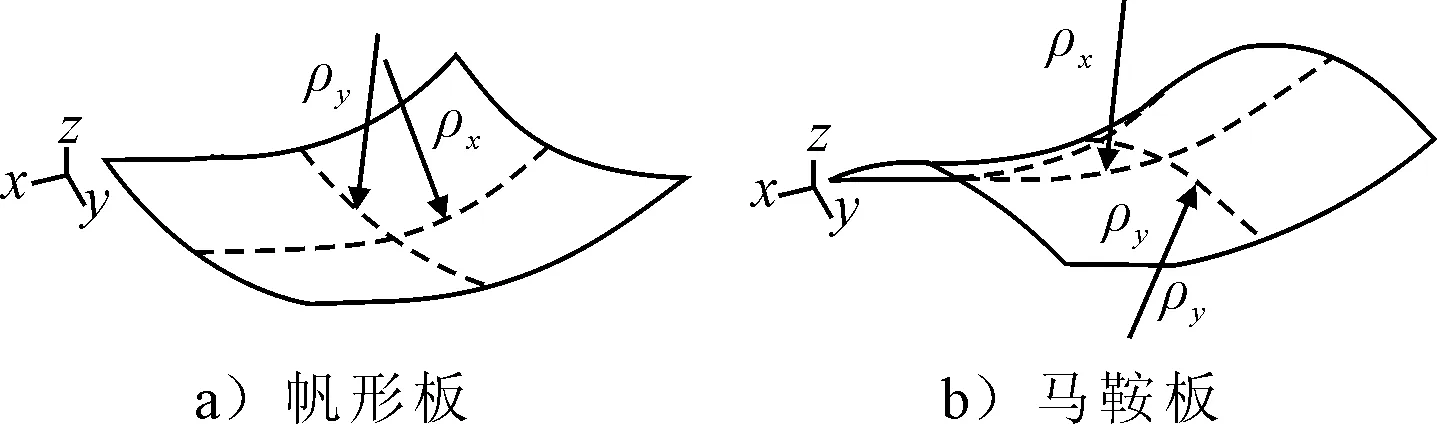
图2 帆形板和马鞍形板材示意图

冲压成形的帆形板满足的曲面方程为

(13)

马鞍形板满足的曲面方程为

(14)

所有实验板材的曲面式(13)、式(14)的相关参数见表1，其中的马鞍形板y方向曲率半径前的负号代表曲率方向与x方向相反.

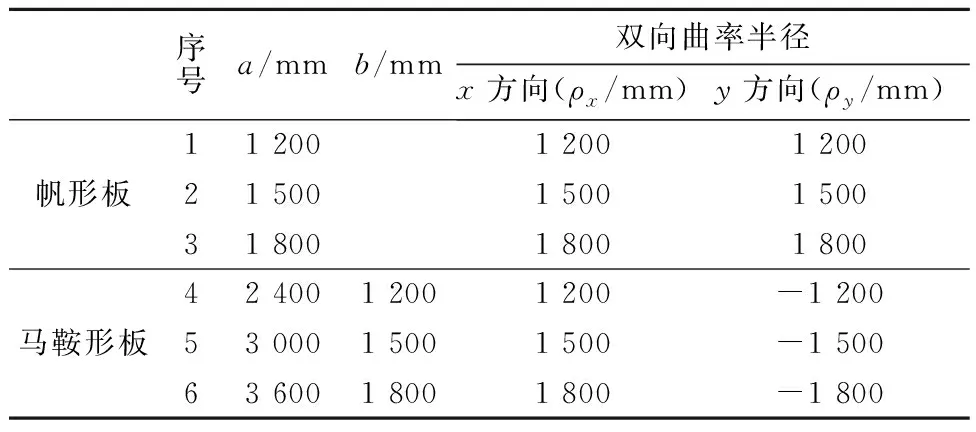
表1 实验板材曲面方程相关参数

双曲度板材冲压成形后所有板材的形状数据均由三维激光扫描仪测量.

2.2 双曲度板材回弹仿真

仿真过程中对武汉理工大学三维数控弯板机进行冲压的整个过程建立模型.

3 典型双曲度板冲压成形回弹的实验结果

对所有实验的双曲度板，计算出x，y方向上的回弹比均值，见表2.

表2 Invar钢帆形板和马鞍形板的双向回弹结果

根据表2中的所有双曲度板回弹均值数据可以得出对于双向曲率相同的Invar帆形板和马鞍形板的实验结果回弹比均值随曲率半径变化图见图3.

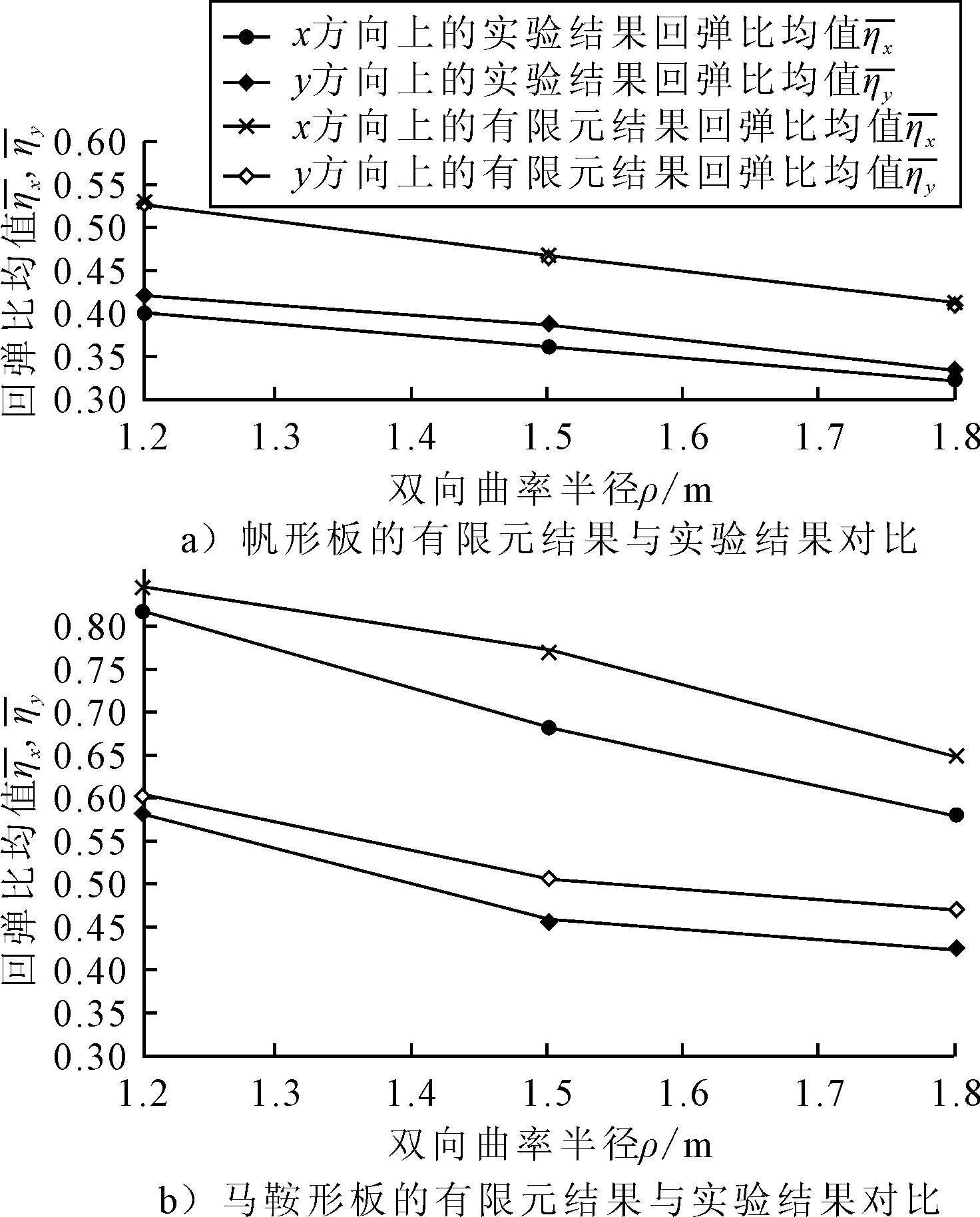
图3 双向曲率相同的Invar帆形板和马鞍形板回弹比均值结果随曲率半径变化图

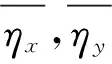
双曲度板冲压成形时两个方向的变形有相互影响，其在两个方向的回弹也有相互影响.双曲度板回弹中的两个方向的相互作用是双曲度板回弹与单曲度板回弹最大的不同.正是这种相互作用使得双曲度板材的回弹机理非常复杂，其回弹补偿也更加困难.但是通过本文提出的双曲度板理论计算模型，可以反映出板材在这种双向耦合作用下回弹量的大小，表现出板材在两个方向上的形状变化.

4 结 束 语

对于可重构模具双曲度板的冲压成形，本文建立了双曲度板材的理论分析模型，比较了帆形板和马鞍形板加工成形中的回弹差异.进行了6组双曲度板的冲压回弹实验和有限元仿真，并通过每个板材上的离散点在两个方向的回弹比均值描述了一系列双曲度板材一次冲压回弹的结果.通过两个方向上回弹比均值的对比发现，实验结果中的帆形板在曲度加工方向的回弹显著大于马鞍形板的回弹.对帆形板和马鞍形板的回弹差异进行了理论分析，这种差异认为是双向曲度在成形过程中由于双向耦合作用而造成的.本文可以为双曲度板材的回弹补偿提供理论指导，从而达到减少冲压次数，提高成形效率的目的.