船型小样本结合近似模型的阻力性能优化

黄国富,张乔宇

(1.中船重工节能技术发展有限公司,上海 200001；2.中国船舶科学研究中心，江苏 无锡 214082)

采用近似模型对优化问题进行求解是解决CFD计算优化时间长 、计算资源高的一种有效途径[1-2]。国内外学者已开展了该方法对于水动力性能优化的相关研究[3-5]，但大多是基于大量的船型样本点对近似模型进行构建，虽然可以保证近似模型的预报精度，但样本集的构建时间较长，减弱了近似模型进行船型优化的优越性[6]。因此，本文提出了一种基于敏感度分析的拉丁超立方的船型小样本选取方式，与以往常用的拉丁超立方、正交试验设计选取的船型小样本集分别构建响应面近似模型，对模型的预报精度和优化效果进行考察。本文船型样本集的构建以Wigley船型在设计航速下的兴波阻力系数作为预报目标，取自由变形法的船体线型变换参数为近似模型的设计变量。

1 基于敏感度分析的拉丁超立方设计

试验设计是数理统计学科中研究如何在减少随机误差、保证试验数据科学性的前提下，根据实际需要收集试验数据从而可以有效降低计算资源、时间成本的方法。目前在船型优化中应用广泛的样本点选取方式主要为正交试验设计、拉丁超立方设计等。正交试验设计的基本思想是根据试验变量对目标的敏感重要性确定出变量水平，利用正交表挑选出均匀分散、整齐可比的试验点，但样本点数量受设计变量个数和水平数的限制，三者需满足特定的数学关系[7]；拉丁超立方设计的本质是根据设定的样本数，对所有变量进行等概率分层抽样，从而确保所有变量在其任意分层区间内都有一个值与之相对应[8]，然而单纯采用拉丁超立方选取小数量船型样本时，样本分布会较为分散，设计方案代表性较差，导致所建近似模型精确度较低。本文采用一种基于敏感度分析的拉丁超立方设计方法，结合具体问题进行设计变量分析，根据变量的敏感度高低进行不同水平的分层拉丁超立方抽样，可在选取小数目船型样本集的同时，一定程度上保证样本点的均布性及代表性。

1.1 敏感度分析

设x1,x2,…,xn为设计变量，ximin与ximax(i=1,2,…,n)分别为对应变量的上下限，则变量xi的敏感度系数计算公式为

(1)

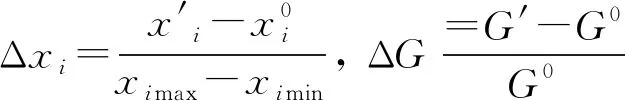
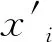
1.2 拉丁超立方设计

在进行变量敏感度分析后，根据具体实际问题，确定出高低敏感度变量(m维)的水平数(P)和样本数目K(P≤K)。对于其余的n-m维变量，根据各自的变化范围等分为K个区间，在每个区间进行等概率抽样，抽样概率为1/K。为确定出各区间内样本点的具体位置，在[0,1]内产生K个随机数Ui(i=1,2,…,K)，与第k个区间对应的随机数Uk为

(2)

将所产生的P个m维变量、K个n-m维变量进行不重复的随机组合，可得最终的K个样本点。

2 近似模型设计

2.1 母型船兴波阻力数值计算

Wigley船型的定义公式为

(3)

(-L/2≤x≤L/2,-H≤z≤0)

式中：x正向表示船体前进方向;z正向表示垂直向上;L为船长;B为船宽;H为吃水,B/L=0.1,H/L=0.062 5，船型方形系数为Cb=0.44，设计航速状态下Fr=0.316。在基于Rankine源基础上的SHIPFLOW软件Xpan模块下进行设计航速下的兴波阻力计算[9]，船体面元网格和自由面网格的划分情况见图1～2，不同航速下兴波阻力系数的计算值和试验值的对比情况见图3。在Fr为0.31～0.4之间，计算所得兴波阻力系数与试验值的误差较小，且变化趋势基本一致，可为后续建立近似模型训练样本，开展兴波阻力优化工作提供保证。

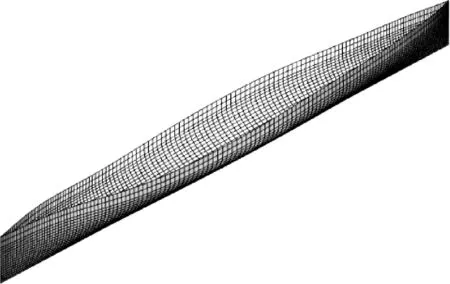
图1 船体面元网格

图2 自由面网格

图3 兴波阻力系数计算值与试验值对比

2.2 船型参数空间建立

采用自由变形法(free form deformation，FFD)对船体曲面参数化。FFD方法是一种灵活的三维几何变形方法，该方法将变形区域线性嵌入到长方体格子中，通过控制格子顶点使船体部分发生形变[10]。选取8组设计变量对船体艏艉部分进行线型变化，几何重构示意图见图4，设计变量变化范围见表1。

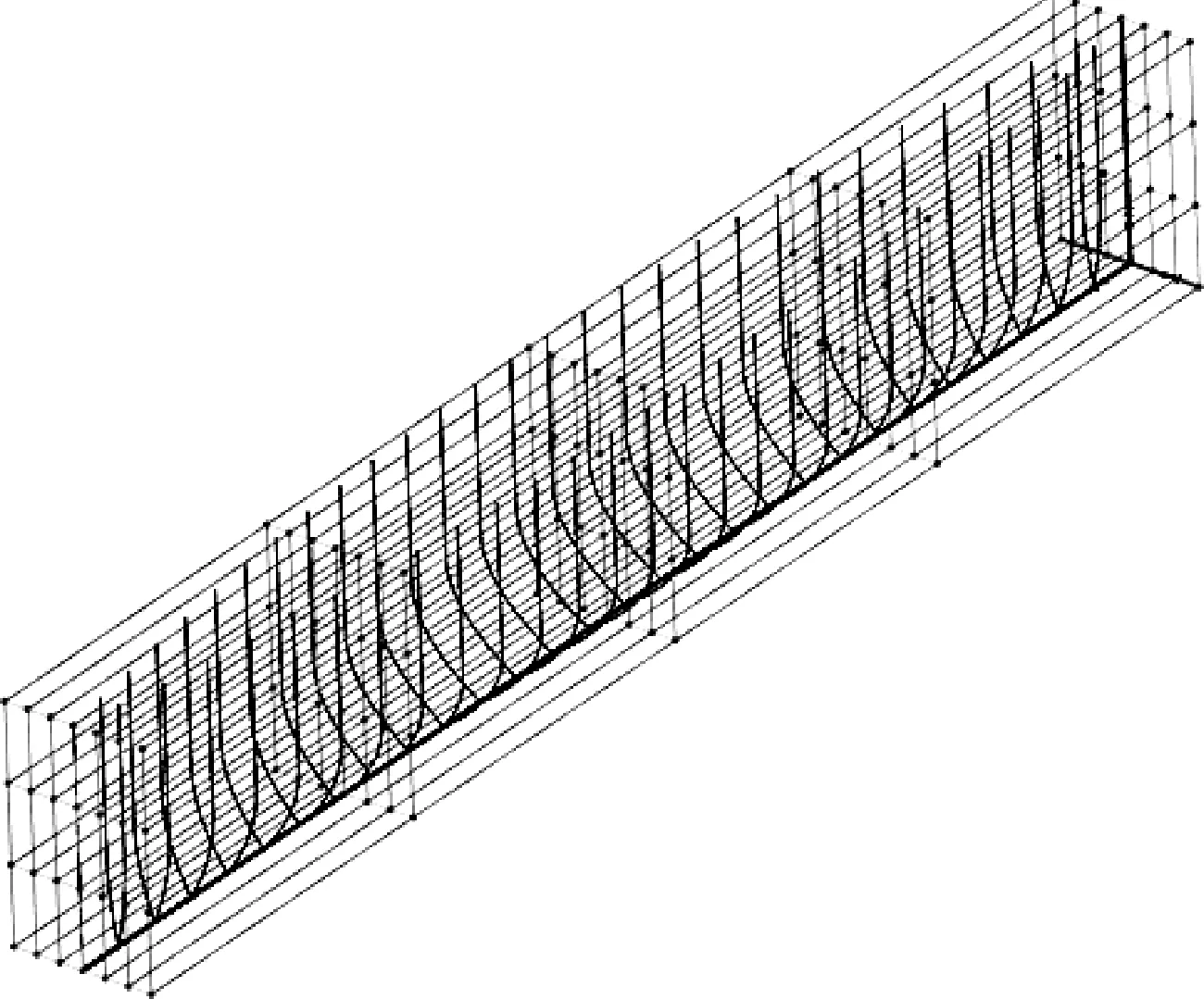
图4 船体几何重构示意

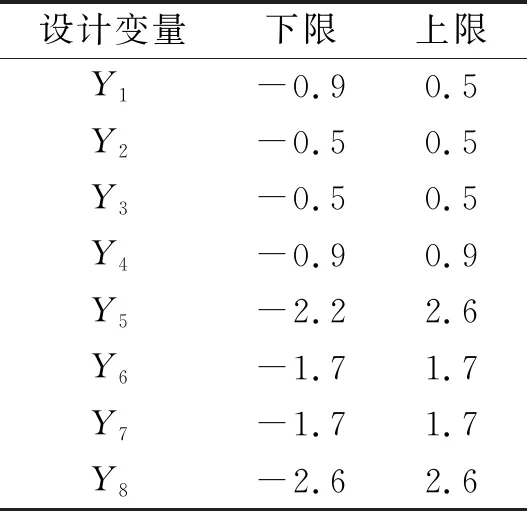
表1 设计变量变化范围

2.3 响应面模型精度对比

分别采用拉丁超立方设计、正交试验设计和基于敏感度分析的拉丁超立方设计方法选取船型小样本集，采用舍去交叉项的二次多项式响应面进行近似建模。为了验证响应面模型的准确性，分别计算样本点拟合预测的平均绝对误差(MAPE)和置信区间，其定义分别为

(4)

(5)

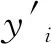
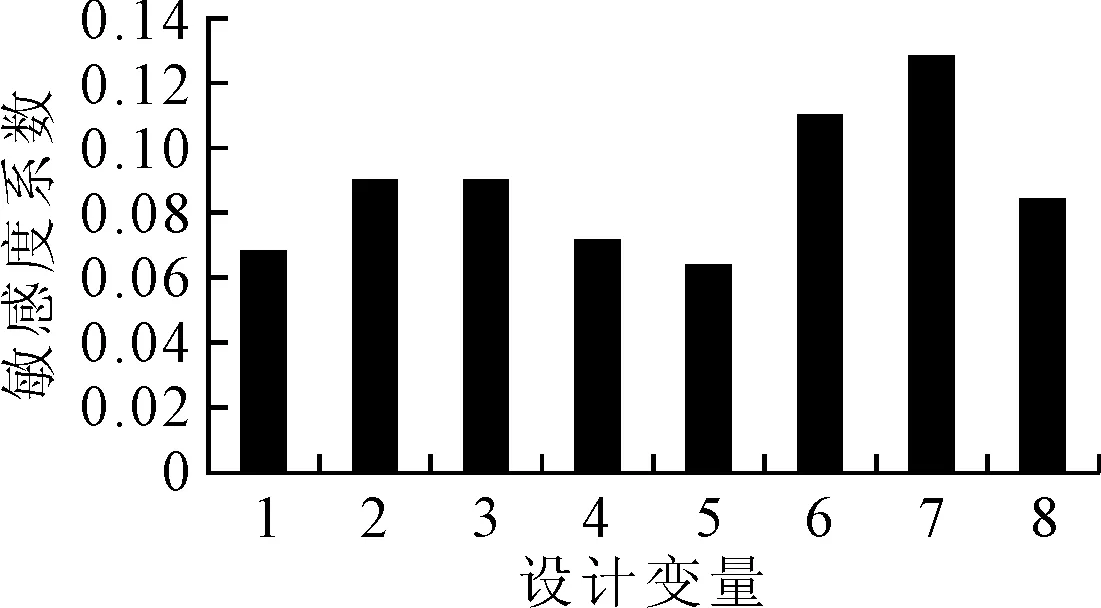
图5 设计变量敏感度分布

表2 正交试验设计抽样

表3 拉丁超立方抽样

表4 基于敏感度分析的拉丁超立方抽样

根据训练样本构建多项式响应面模型，各分项系数见表5～7，拟合预测的平均绝对误差和置信区间见表8～9。为了进一步验证近似模型的精度，另外随机选取100个测试样本，分别采用CFD计算及响应面模型对兴波阻力系数进行求解，结果见表10～11。

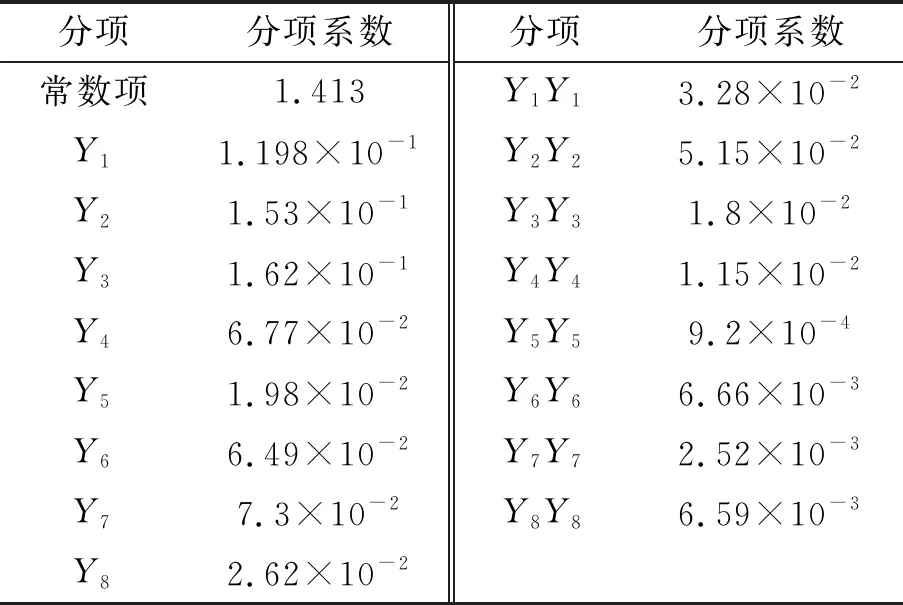
表5 拉丁超立方构建的响应面

表8 响应面预测平均绝对误差

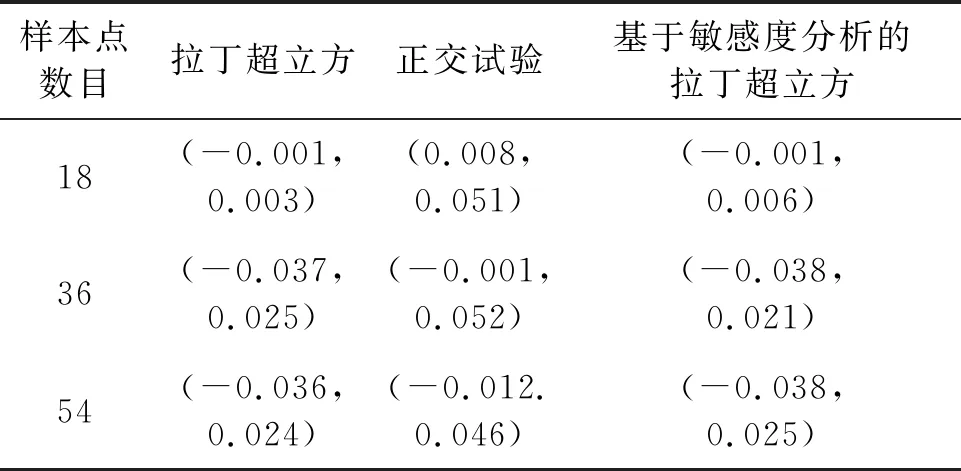
表9 响应面预测置信区间

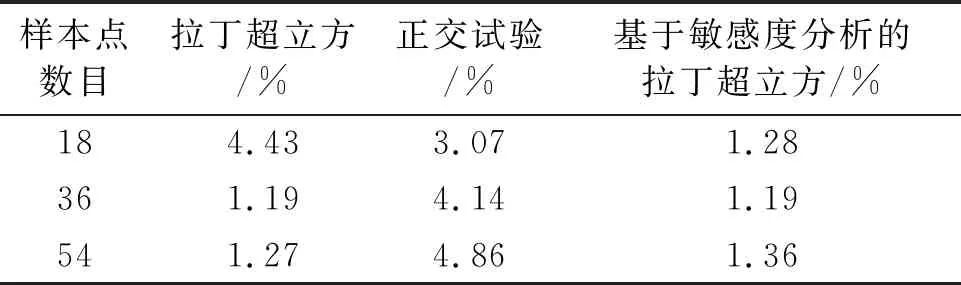
表10 测试样本预测平均绝对误差

表11 测试样本预测置信区间

上述结果表明，采用正交试验设计方法选取的样本虽然保证了均布性，但在样本数量较少时设计变量选取水平有限，所构建的近似模型精度较低；拉丁超立方设计方案的样本均布性与变量水平相比正交设计均得到了明显提升，但样本点的选取随机性较大，没有对敏感度高的设计变量进行重点考察，所构建的近似模型虽然对训练样本预测精度较高，但对于测试样本的预报误差较大，随着训练样本数目的增多，其预报精度有所提升；而基于敏感度分析的拉丁超立方设计的小样本，根据变量敏感度高低进行分层采样，既保证了样本选取的均布性，又使得样本方案具有代表性，所构建的近似模型对于训练和测试样本均表现出较好的预测效果。

3 设计航速下的船型优化

在设计航速下分别采用CFD方法与响应面模型对Wigley艏艉线型进行优化，响应面模型采用基于敏感度分析的拉丁超立方抽取的18组样本进行构建。优化目标函数的数学模型为

Cw=minf(Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8)

(6)

为满足船舶浮态要求，除设计变量满足表1要求外，排水量、湿表面积和浮心纵向位置均不超过原型的1%，优化算法采用单目标遗传算法。在CFD方法的优化过程中，种群数量设置为20，终止代数为50，交叉变异概率分别为0.8和0.06,在经历了20 h的优化时间后，得到最优解船型Ⅰ。同时采用响应面方法，优化设置不变，经历了0.25 h优化时间后得到优化船型Ⅱ，优化迭代过程见图6～7，优化船Ⅰ、Ⅱ的结果对比见表12。由此可知，响应面的优化结果经CFD计算验证，兴波阻力系数误差仅有1.3%，精度满足工程要求。图8～9展示了优化船Ⅱ与母型船的波切面图和兴波波形图，可以看出优化后船体周围波形数减少，波形切片幅值降低，近似模型方法仅需通过CFD计算18组训练样本的兴波阻力，减少了约96%的计算成本，较单纯采用CFD技术直接优化，优化效率和质量均得到明显提高。

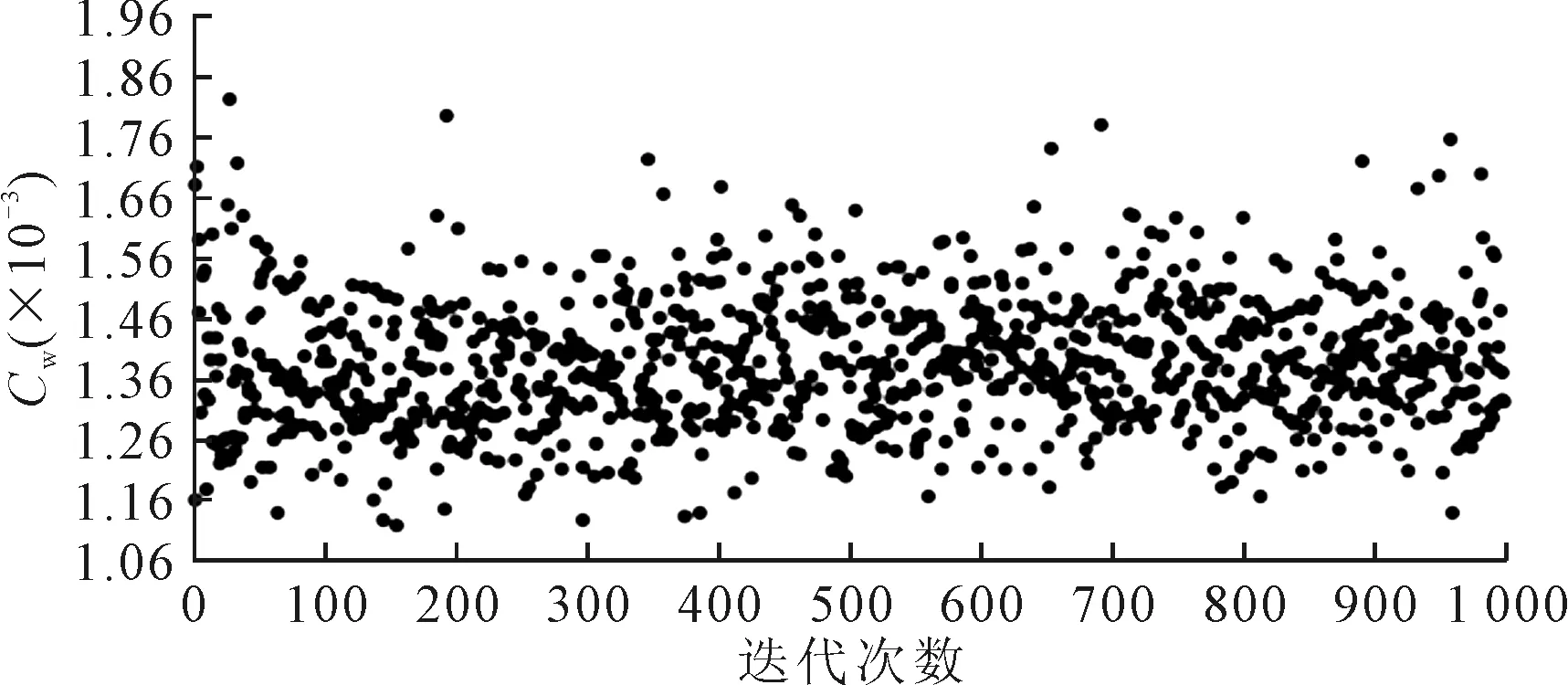
图6 CFD方法优化过程

图7 响应面模型优化过程

表12 CFD技术与近似模型优化结果对比

图8 波切面对比

图9 波形对比

4 结论

在选取船型小样本时，根据实际问题对设计变量进行不同程度的分层均布抽样，可以构建出精确度较高的近似模型。除文献中采用近似模型进行船型优化的类似工作外，本文还着重探究了如何在选取船型小样本条件下构造出高精度近似模型，并取得了较好的应用效果，明显提升了优化效率和质量，可为结合近似模型的船型优化工作提供参考。采用近似模型进行船型优化还有许多问题值得进一步研究，如响应面近似模型对于不同船型变换方式的适应性、高精度近似模型的形式选取等。