坐底式深水网箱振动实测信号分析处理方法

宋嘎，王娜娜

(1.山东职业学院，济南 250104；2.烟台汽车工程职业学院，山东 烟台 264000)

在实际的深水网箱使用过程中，由于受到复杂的海洋环境影响，结构振动信号复杂多变，往往呈现非稳态信号的特征，同时信号中还会包含有各种噪声成分，给深海网箱结构的监测带来了很多难题。在海洋环境中，大多数的测试信号是时变的非平稳信号，仅使用传统的傅里叶变换进行频谱分析已经无法满足实际要求，需要在时域内观测结构真实模态的变换信息，提高对深水网箱结构实测信号的分析能力,即进行时频分析[1]。通过时频分析，可以完整刻画信号在时间和频率轴上的能量强度分布——联合时频分布[2]，以及结构振动频率随时间的变化情况，提供信号的局部特征，从而实现对深水网箱结构的安全检测[3]。有学者开展的相关研究[4-6]。

本文在传统变分模态分解的基础上，通过引入相关性分析及频域最大值分析，提出一种自适应设置模态阶次的变分模态分解方法，根据信号的特征自动确定模态阶次。利用Matlab软件进行编程，并将该方法应用于实测的深海网箱振动信号，证明该方法在处理深海网箱实测振动数据时的有效性及在对深海网箱结构进行安全监测时的应用价值。

1 变分模态分解

变分模态分解可以将非稳定的多成分信号分解为在中心频率处的有限带宽成分信号，每个分离出的成分即为有限带宽的固有模态函数。假设信号y(t)中包含k个分量xk，且每个分量的中心频率为ωk，各分量通过求解下式的约束变分模型得到：

(1)

式中：*为卷积运算;δ(t)为Dirac分布。

引入拉格朗日乘法算子λ，式(1)可以转化为非约束变分问题

L({xk},{ωk},λ)=

(2)

式中：α为二次惩罚因子，可以约束数据的保真度。同时，在算法中嵌入维纳滤波器，以避免计算过程中受采样频率和噪声的影响。为了求解变分问题，采用交替方向乘子进行计算，同时定义收敛准则：

(3)

k阶分量可以通过下式求得：

(4)

(5)

2 自适应变分模态分解算法

2.1 频域最大值分析

当模态阶次设置较少时，会导致一个模态内存在多个频率成分，在分解过程中，需要对分解出的成分进行分析，判断成分内是否发生模态混叠，检验其是否分解完全。在本方法中，选用各成分在频域内极大值的个数和幅值大小进行判断。引入筛选准则ξ：

(6)

2.2 相关性分析

利用变分模态分解时，若模态阶次设置过小，会造成欠分解问题，导致信号中的真实模态难以分离出来。因此，通过引入相关性分析，进一步确定模态阶次。相关性系数ρ定义如下。

(7)

式中：yc为重构信号；y为原始信号；E为期望。

当相关系数较小时，欠分解问题发生，需要继续增加模态阶次。

2.3 算法流程

1)设置变分模态分解的参数，一般惩罚因子α设置为2 000。

2)设置模态阶次k=1，并利用变分模态分解进行第一次分解，得到一个分量记为IMF1。

3)对IMF1进傅里叶变换，并在频域内求出所有极值点的大小。

4)设置筛选准测ξ，当极值点间满足该筛选准则，则认为此时模态阶次k满足要求，若不满足该筛选准则，则增大模态阶次k并重新进行变分模态分解。

5)当分解满足筛选准则时，对分解出的k个成分进行求和并计算重构信号与原始信号的相关性，若相关性满足阈值要求，则认为此阶次较为合适，若不满足，则继续增大阶次，重新进行变分模态分解。

3 实测数据分析

3.1 结构介绍

测试结构见图1，为位于渤海海域的某坐底式深水网箱。该网箱容积60 000 m3，长66 m，宽66 m，最大吃水30.5 m。采用坐底式四边形钢结构形式，设计使用寿命10年。该网箱集成了网衣自动提升、自动投饵、水下监测、网衣清洗、成鱼回收等自动化装备，最大程度保证网箱的安全性和经济性。除智能养殖功能外，网箱还兼具休闲旅游的功能。网箱上方建筑采用了双层生活区模块化建筑，有效提升了生活区利用率，周边走台进行加宽设计，生活区内采用高标准“中国风”装修风格，可同时满足30人休闲垂钓和观光旅游需求，给客户以舒适的度假体验。测试时在四根立柱处分别安装三向加速度传感器进行测量。测试时间为260 s，采样频率为250 Hz。选择其中一个传感器的y方向测试数据进行分析，测试加速度信号的时域图和频域图见图2。

图1 测试的深海网箱结构

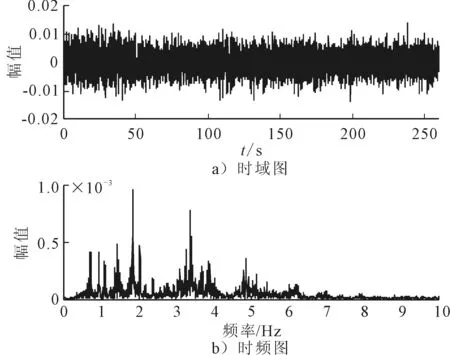
图2 测试信号y方向的时域图和频域图

3.2 分析结果

在信号分析过程中，通过使用自适应变分模态分解技术对50～90 s，共10 000个点的信号进行分解，当模态阶次增加到等于86时，分解结束。对前3个成分进行展示。

由图3可见，由改进的变分模态分解方法分解出的第一个成分对应于图2中的一阶模态，从该成分的时域图中(图2a))可以看到该信号较为稳定，对提取出的成分进行Hilbert变换可以得到该成分的时频图，见图3b)。从时频图中可以看到该成分的信号频率在1.8 Hz左右，同时在整个时间范围内，该实测的振动信号表现出了较大的时变性。

图3 信号分解后得到的第一阶模态

对分解出的第二个成分和第三个成分进行Hilbert变换，得到其时域图和时频图，见图4、5，可以看到2个成分分别对应于3.3 Hz和5.2 Hz。与图3对比可以发现，结果与整个信号在频域内的结果一致。在图3中，由于频域方法的局限性，无法展现信号频率随时间的变化情况，这个问题在所提出方法中也得到了解决。

图4 信号分解后得到的第二阶模态

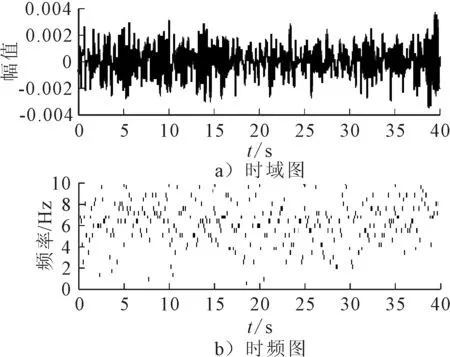
图5 信号分解后得到的第三阶模态

为了进一步验证该方法的有效性，对分解的信号进行重构，并与原始信号进行对比，对比结果见图6。为了使结果更加清晰，在图6中对10～10.3 s的部分信号进行放大展示，可以看到，原始信号与重构信号吻合较好。利用式(7)计算重构信号与原始信号之间的相关性，可以得到此时相关系数为0.997 4，证明所改进的方法在处理深水网箱实测振动信号的有效性。

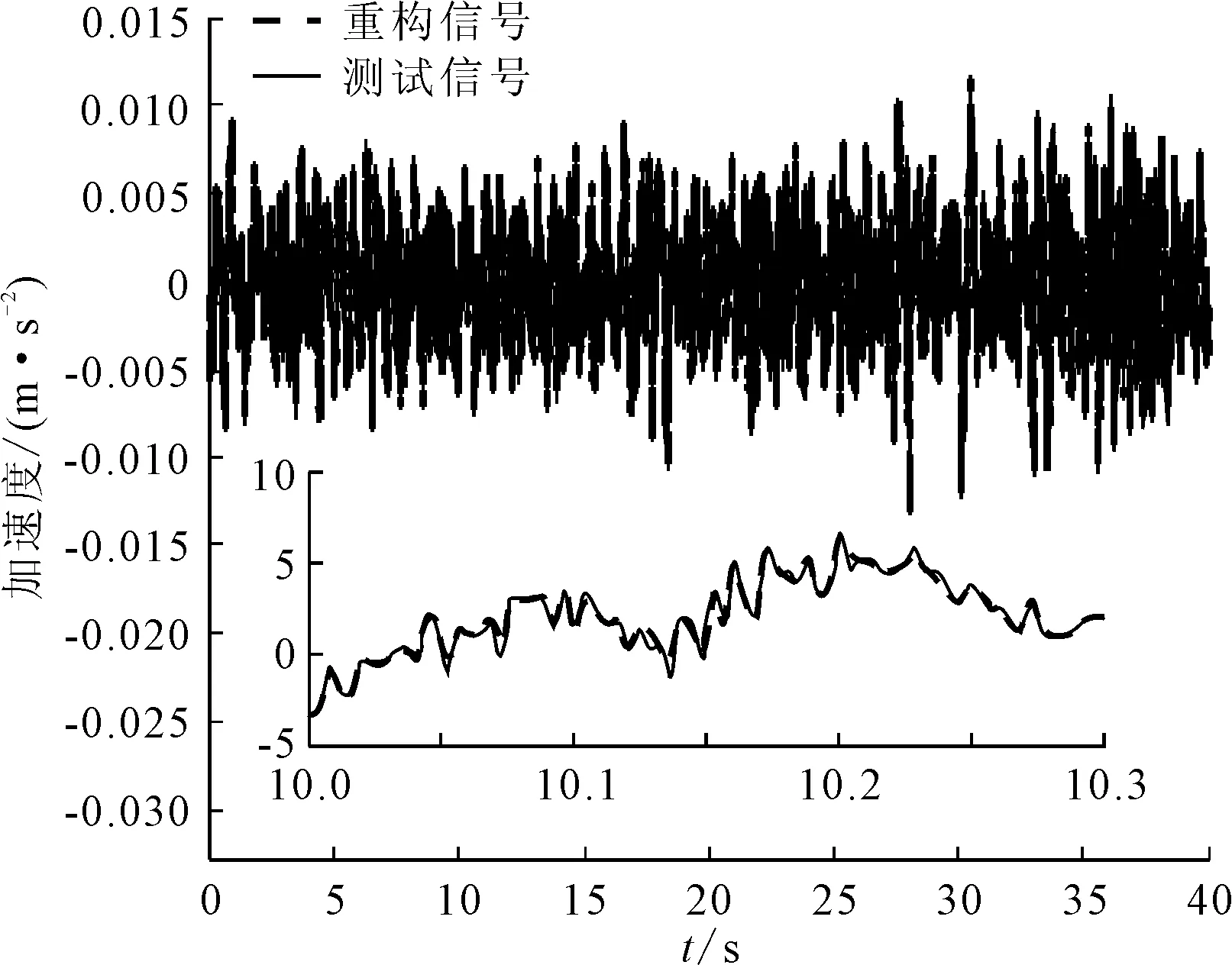
图6 重构信号与原始信号

4 结论

在传统变分模态分解方法中，一个主要的局限性就是其需要预先确定模态阶次。本文针对这一局限性，引入了相关性分析及频域最大值分析，提出一种自适应的变分模态分解技术。在分解过程中，由于使用了维纳滤波器，使得该方法具有去噪能力。通过相关性分析和频域最大值分析，该方法可以最小化所有固有模态函数的频谱宽度之和，实现基于变分模态分解的信号最优分解。通过利用该方法对实测得到的深水网箱振动信号进行分解，并通过Hilbert变化可以得到分解模态的时频图。结果显示，深水网箱实测信号具有较强的时变性。使用本文的方法可以对深水网箱信号进行很好地分解，也证明该方法在深水网箱结构的安全检测中的潜在价值。

虽然改进的变分模态分解方法可以自适应的设置分解阶次，其本质仍然为变分模态分解，因此，在变分模态分解中存在的其他缺陷在本文方法中仍然存在，例如端点效应，模态混叠等问题。因此，如何克服这些缺陷，使用改进方法对深水网箱的实测信号进行更为有效地分解，将作为今后的重点进行研究。