高温高压屏蔽泵用电动机可倾推力轴承水膜计算与分析
2020-07-29刘丁元郭小佳
刘丁元,郭小佳
(佳木斯电机股份有限公司,黑龙江佳木斯 154002)
0 引言
泵用电动机(以下简称核电动机)是反应堆压力边界的一部分输送介质为反应堆冷却剂,含有放射性。当易损件到达寿命时,需停堆维护。轴承做为核主泵电机的关键易损件,其设计直接关系机组寿命进而影响电站运行的经济性和工作人员的身体健康,故轴承设计是电机关键技术,轴承设计中动压润滑水膜计算尤为重要。目前,已有不少学者对多级泵滑动轴承液膜的特性展开了相关研究,余江波[1]对轴承水膜润滑机理进行了研究,冯慧慧[2]基于有限差分法对水润滑主泵轴承进行了细致分析,根据流体动压润滑理论[3、4]。本文基于Matlab编程求解二维定常Reynolds方程,对方程进行差分离散化,得到核主泵电动机可倾推力轴承水膜压力分布与水膜厚度分布,研究在不同转速和轴向载荷下,水润滑轴承水膜厚度分布变化规律,并得到相互关系曲线,对指导可倾推力轴承设计具有重要的工程意义。
1 电动机可倾推力轴承结构概述
轴承结构轴承运行80℃去离子水换将,选择M209K与镍基合金组成摩擦副。在目前有成熟应用经验的材料中,石墨基体浸渍呋喃树脂材料M209K,具有良好的自润滑性能与导热性能、抗冲击性能、耐辐照性能。
推力盘的下方设置下推力轴承,机组产生的剩余轴向力由下推力轴承承受。下推力轴承由8块扇形瓦块组成,每块扇形瓦均安装在单独对应的瓦座内,并用挡板、螺钉压紧。在止推轴承座下方有圆轴承支座和支座,支撑在止推轴承座偏心位置,使下推力轴承工作时自然形成水楔倾角,具有较大的承载能力。主泵电动机下推力轴承结构见图1。

图1 下推力轴承结构(右侧为三维示意图)
2 可倾推力轴承扇形瓦面动压润滑理论模型
本文以可倾推力轴承扇形瓦点支承推力轴承为研究对象,依据流体动压润滑理论,建立了水膜压力方程(雷诺方程)、水膜厚度方程、粘温方程。图2为可倾推力轴承单个瓦面简化示意图。
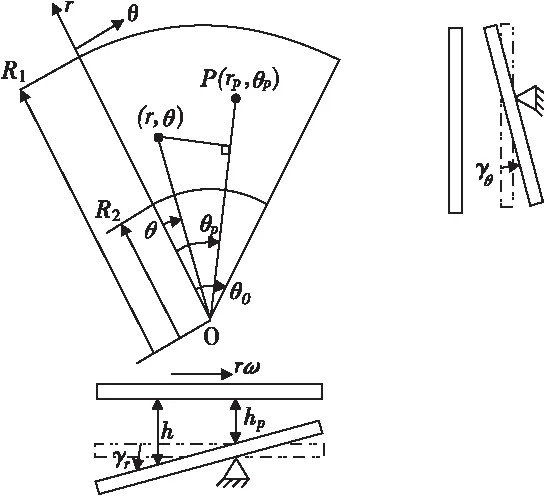
图2 推力轴承单个瓦面简化示意图
2.1 水膜压力方程(雷诺Reynolds方程)
基于流体流动物理守恒定律,从粘性流体力学的连续性方程和动量方程出发,采用一定的合理假设可推导出的雷诺微分方程,Reynolds方程描述了水膜压力分布与水膜厚度、流体粘度、流体速度之间的数学关系。其假设条件如下
(1)不考虑瓦块与推力盘的变形;
(2)推力盘与瓦块间的水膜层很薄,水膜压力在水膜厚度方向上被视为常量;
(3)润滑水与固体面间没有相对滑移;
(4)润滑水除粘度外,其它物性参数不变,属于牛顿流体;
(5)润滑水的彻体力和惯性力与水性力相比,可以忽略不计;
(6)润滑水不可压缩;
(7)润滑水流动为层流流动。
在此基本假设下,柱坐标下的水膜压力方程即雷诺方程为

(1)
一般情况下,沿水膜厚度方向的速度为0,即沿Z轴的速度W1=W2=0,推力瓦的速度U1=0,镜板的速度U2=ωr。同时,应用极坐标形式将式(1)简化为
(2)
式中,μ—润滑水动力粘度;P—水膜压力;ω—滑动盘转速;h—润滑水水膜厚度;r、θ—极坐标系下水膜任一点坐标。边界条件为
(3)
式中,Γ—水膜边界;Γ1—水膜破裂边界。
2.2 膜厚方程
根据点支撑推力轴承扇形瓦结构,导出瓦块倾斜时,瓦面上任意一点处的水膜厚度方程
h=hρ+γr[rsin(θρ-θ)]+γθ[rcos(θρ-θ)-rρ]
(4)
式中,h—瓦面上任意一点的水膜厚度;hρ—扇形瓦支点P处的水膜厚度;γr—瓦绕OP线的转动角;γθ—瓦垂直于OP线的转动角;r—瓦面上任意一点的半径;θ—瓦面上任意一点的轴向角;θρ—扇形瓦支点P处的周向角;rρ—扇形瓦支点P处的半径,示意图见图2。
2.4 温粘方程
温粘关系采用Walther-ADTM方程,方程为
lglg(ν+0.6)=A0-B0lg(T+273.15)
(5)
式中,A0、B0—实验确定出的系数;ν—运动粘度。水的物理参数为: 其实际运动粘度为44.1mm2/s,密度为871kg/m3,系数A0=11.176254,B0=4.390936。
3 基于Matlab推力轴承润滑性能计算分析
根据前文建立的有关扇形可倾瓦点支承推力轴承润滑性能的数学模型以及基于有限差分法离散形式的基础上,本文应用 Matlab编制了可倾推力扇形瓦点支承推力轴承润滑性能数值计算程,推力轴承结构参数见表1。

表1 推力轴承结构参数
3.1 额定工况电动机可倾推力轴承润特性计算结果
额定工况电动机可倾推力轴承润滑静特性计算结果见图4。
由图3知,最大水膜厚度187μm,出现在推力轴承扇形瓦进水处,最小水膜厚度48μm位于推力轴承扇形瓦左上方,水膜厚度从推力轴承扇形瓦右下方左上方呈现减小趋势,水膜厚度分布沿上述方向分布与主泵电动机旋转方向相关,同时分布规律与上文式(4)膜厚方程相符。水膜压力分别沿推力瓦径向与周向沿抛物线分布,水膜压力在推力瓦进口处先缓慢增加到最大值0.166MPa在推力瓦出口处急剧减小,由雷诺方程边界条件式(3)可知,可倾推力轴承扇形瓦四周边缘的压力为初始值,即为0。

图3 定工况可倾推力轴承扇形瓦水膜厚度与压力分布

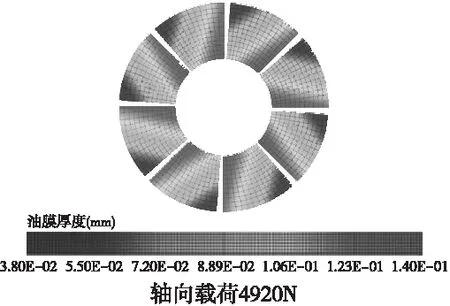
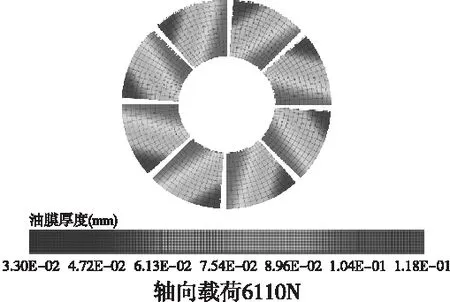

图4 倾推力轴承扇形瓦水膜厚度分布(不同载荷)
3.2 主泵电动机轴向载荷对水膜厚度影响
如图4,在主泵电动机推力扇形瓦,扇形瓦结构参数(包括瓦数、周向与径向倾角、扇形瓦内、外径)与转速恒定,轴向载荷分别为3970N、4920N、6110N、7050N时,润滑水膜厚度分布情况,可知,3970N对应最小水膜厚度为44μm、4920N对应最小水膜厚度为、6110N对应最小水膜厚度为33μm、7050N对应最小水膜厚度为30μm,故水膜厚度与轴向载荷呈反相关,关系曲线见图5。
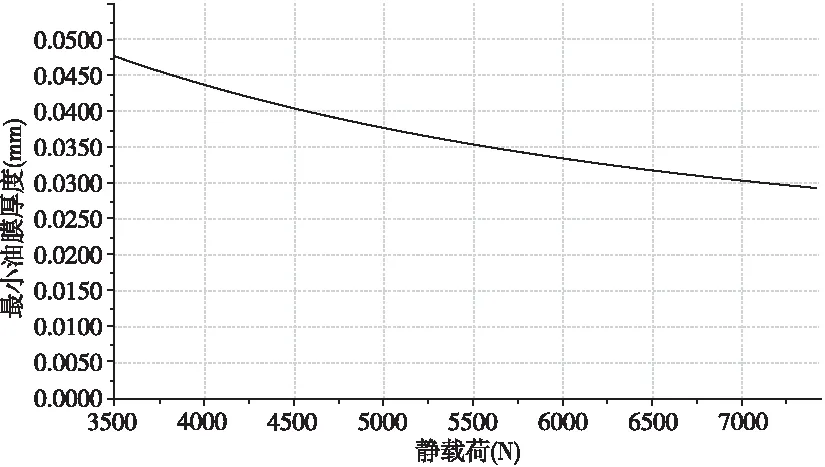
图5 水膜厚度与轴向载关系曲线
3.3 主泵电动机转速对水膜厚度影响
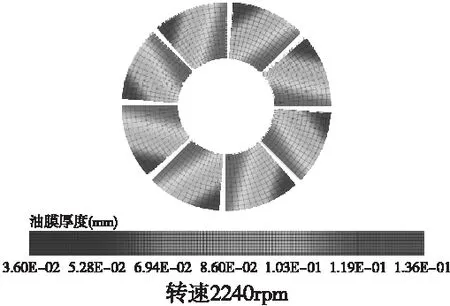
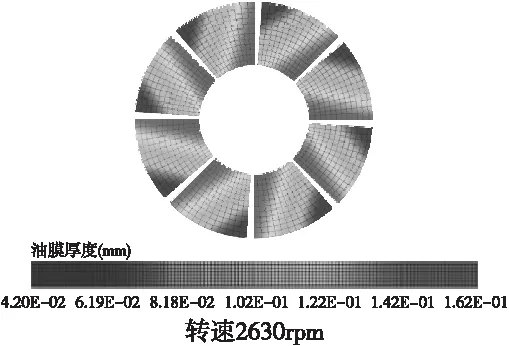
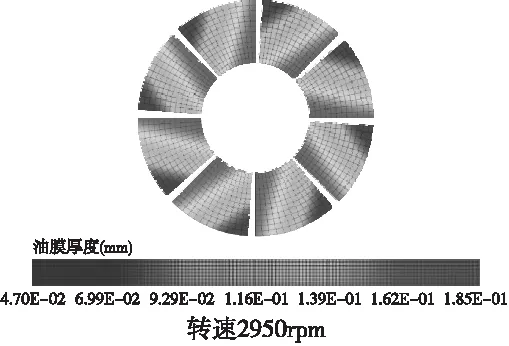
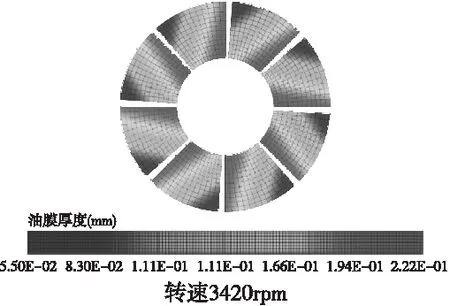
图6 可倾推力轴承扇形瓦水膜厚度分布(不同转速)
图6可知,在主泵电动机推力扇形瓦,扇形结构参数(同上)与轴向载荷恒定,转速分别我2240rpm、2630rpm、2950rpm、3420rpm所对应最小水膜厚度分别为36μm、42μm、47μm、55μm,水膜厚度与转速增加而增大,关系曲线见图7。
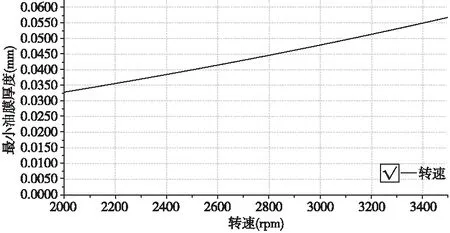
图7 水膜厚度与转速关系曲线
4 结语
本文以某型主泵可倾推力轴承为例,介绍了推力轴承结构,根据流体动压润滑理论,编制基于Matlab有限差分法程序,计算得到额定工况下水膜厚度分布、水膜压力分布,并分析了电动机转速、轴向载荷对轴承润水膜厚度的影响,总结如下。
(1)额定工况下,电动机可倾推力轴承水膜厚度从推力轴承扇形瓦右下方→左上方呈现减小趋势,水膜厚度分布沿上述方向分布与主泵电动机旋转方向相关,同时分布规律与膜厚方程相符。
(2)额定工况下,电动机可倾推力轴承水膜压力水膜压力在推力瓦进口处先缓慢增加到最大值0.166MPa,在推力瓦出口处急剧减小,这与雷诺方程边界条件设置一致。
(3)电动机可倾推力轴承润滑水膜厚度比与电动机转速、轴向载荷等因素相关,在一定转速范围内(2200~3400rpm),随着转速的升高,润滑水膜厚度增大。在一定轴向载荷范围内(4000~7000N),润滑水膜厚度随轴向载荷增加而减小。
