基于扩样技术和地理加权泊松回归模型的交通量估计

荆 毅，林航飞

（同济大学道路与交通工程教育部重点实验室，上海201804）

交通流量是交通工程中的基础数据。交通流量的用途包括但不限于交通设施的规划和建设、交通政策的设计和实施、道路碰撞风险的量化和交通污染的评估。正是由于道路交通量的重要性，地方政府投入了大量资金和精力，并采用不同的方法来采集交通流量数据。其中，自动流量检测器（例如线圈检测器和摄像机）是采集交通流量的主要设备。使用流量检测器面临的一个重要问题是存在大量缺失值［1］。首先，出于成本考虑，流量检测器只布设于少数主要道路上，而绝大多数的低等级道路由于没有安装检测器而没有数据。第二，频繁的道路重建，可能会破坏埋在道路下的线圈检测器，导致数据缺失。第三，传输错误和设备故障也可能导致数据丢失。因此，利用有限的交通流量数据来估算整个路网的交通量就显得更加实际和重要。

在以往的研究中，不同研究人员用不同的方法来估计交通量。基于扩展因子的模型是一种传统的交通流量估计方法。在该模型中，根据交通量的变化模式对路段进行聚类，然后利用扩展因子将观测到的交通量扩展到同一个聚类中没有交通量的路段。该方法简单易行，在世界范围内被广泛采用［2］。多元线性回归（MLR）是另一种常用的交通量估计技术。在MLR中，最常用的自变量可分为道路设计特征、社会人口统计特征和土地利用特征［3-4］。此外，还融入了一些基于空间位置的地理特征，例如，Morley等［5］提出了一种由最短路径的通过次数确定的道路重要度特征来预测路网的年平均日交通量（AADT）。随着数据量的快速增长，近年来机器学习算法如神经网络［6］、支持向量机回归［7］和基于树的模型［8］也被用来估计流量。虽然机器学习算法能提供比统计方法更高的精度和效率，但由于其黑箱特性，机器学习结果解释性并不高。此外，越来越多的研究表明，区域内的交通活动之间存在空间相关性，即流量不仅与研究路段的特征相关，而且与相邻路段上的流量相关。因此，能捕捉这种空间相关性的空间模型可以提高流量估计的精度，这些空间模型包括空间插值［9-11］、空间回归模型［12］和地理加权回归模型［12-14］。

地理加权回归模型是一种可以捕捉研究区域内因变量和自变量变化关系的回归方法。与许多全局回归模型不同，地理加权回归模型是为每个研究单元构建一套模型参数［15］。根据因变量分布的不同分为地理加权高斯模型、地理加权泊松模型（GWPR）和地理加权Probit 模型等。其中，地理加权泊松模型更适合于对计数数据（如交通量）的估计［12-13］。

使用空间模型的一个问题是道路网络中可用数据的不平衡分布。由于在估计路段交通量时，还考虑了附近的交通量，因此附近可用数据较少的道路估计性能较差。Eom等［9］采用空间插值算法对北卡罗来纳州非高速公路道路的交通量进行预测，发现在流量检测器密度较高的区域估计性能更好。解决此问题的一种方法是对原始样本数据重新采样以平衡其分布。一些研究证明，在建立空间模型之前采用扩样方法可以提高模型的性能。例如，Tajmajer 等［16］在使用机器学习模型预测交通量之前，先使用基于扩展因子的方法扩大了样本量。Chen等［17］采用合成少数过采样技术（SMOTE）对非主干路上的交通量进行扩样，结果表明，SMOTE有助于纠正样本的不平衡，并显著提高模型的估计性能。因此，在建立空间模型之前解决不平衡观测值问题以提高估计精度是有必要的。

本研究提出采用扩样与地理加权泊松回归相结合的方法来对路网缺失流量进行流量估计。流量数据来源于上海市杨浦区安装的悉尼协调自适应交通系统（SCATS），共计2 217 条车道，其中只有560 条车道有可用流量。首先，采用基于空间相似性的扩样方法来纠正缺失流量的空间不平衡。然后，基于扩样后数据利用地理加权泊松模型估计路网中所有车道的交通流量。最后，为了验证组合模型的性能，采用10 倍的交叉验证方法比较了3 种不同的模型，即 MLR 模型、GWPR 模型以及扩样与 GWPR 组合模型。本文研究结果为在观测值有限且不平衡的情况下提高流量估计的精度提供了一种可行方案。

1 方法

本研究的步骤如下：首先，采用Moran’sI指数来检验不同交叉口的交通量之间是否存在空间相关性。第二，采用扩样技术对空间分布不平衡的流量样本进行校正。第三，在扩样样本的基础上，采用GWPR 方法提取交通流量与各自变量之间的关系。最后，采用10倍交叉验证法验证扩样和GWPR组合模型的有效性。

1.1 Moran’s I 指数

Moran’sI指数广泛用于检验线性回归的残差之间是否存在空间自相关［18］。本研究采用R语言中的“spedp”包来计算。Moran’sI指数的范围在-1到1之间，表示不同的空间相关类型。

（1）0＜I≤1：正相关，在空间上表现为高值（低值）样本与高值（低值）样本聚集。

（2）-1≤I＜0：负相关，在空间上表现为高值样本与低值样本聚集。

（3）I=0：不相关，在空间上表现为高值或低值样本随机分布。

1.2 基于空间相似性的扩样方法

本文提出了一种新的基于空间相似性的扩样方法来扩充流量样本。首先，定义空间相似性指标dij，如公式（1）所示；然后，对于缺失流量的车道i，计算车道i与其他有流量车道的空间相似性；最后，将空间相似性最高（最小的dij）对应车道的流量作为车道i的流量。

车道i和车道j的空间相似性定义为

式中：Sij为空间相似性；Xi为车道i终点的X坐标；Yi为车道i终点的Y坐标；Fik为车道i的第k个特征；Fjk为车道j的第k个特征。考虑到车道特征的不同尺度，在计算空间相似性之前，需要对所有特征进行min-max规范化。

1.3 地理加权泊松回归（GWPR）

GWPR采用由距离定义的权重矩阵来处理空间自相关问题。在估计中，样本附近的观测值具有更高的权重。GWPR 为每一个样本估计一组局部参数。本研究使用R语言中的“spgwr”包对GWPR模型的进行估计。GWPR模型定义如下：

式中：yi为样本i的因变量向量（i=1，2，…，n，n为样本总数）；xki为样本i的第k个特征向量；β0i为截距项；βki为相应系数；p为特征（自变量）总数；εi为样本i的误差项。

样本i的估计系数可由下式得到：

式中：Wi为样本i的空间权重矩阵，由公式（4）和（5）计算得到；Y为因变量向量；X为特征矩阵。

本研究采用高斯函数计算空间权重矩阵，它将权重作为距离的连续函数来计算，以确保有足够的局部观测值来估计模型［19］。

式中：Dij为样本i与样本j的欧式距离；n为样本总数；θ为带宽。

2 数据描述

2.1 研究区域和数据来源

本研究以位于上海中心城区东北部的杨浦区为研究区域。杨浦区土地面积60.73 km2，到2016年底拥有 130.94 万居民［20］。当地政府从 1986 年开始引入悉尼协调自适应交通系统（SCATS），对重要交叉口的交通量进行监控和协调信号时间。SCATS 依靠埋在进口车道的线圈检测器实时采集交通量，并根据采集的交通量自动调整交叉口的信号相位，以达到整个交叉口的最佳通行效率［21］。

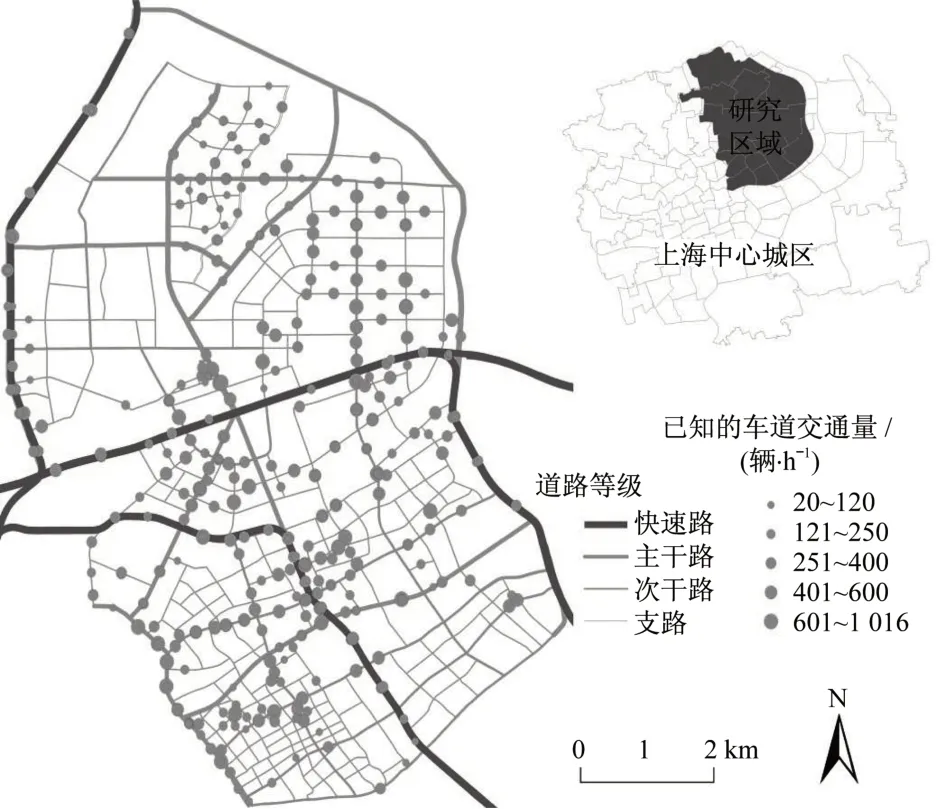
图1 研究区域和已知流量分布Fig.1 Study area and known traffic volume distribution

本研究的路网如图1 所示。地面道路全长308.0 km，其中主干道占14%，次干道占23%，支路占63%。此外，该区还有20.5 km 的快速路。车道流量来自于2016年10月11日的SCATS流量数据。研究区共有2 217条车道，但只有560条具有完整的流量。如图1 所示，具有已知流量的车道主要分布在等级较高的路段，这是合理的，因为在路网中高等级道路更有可能获得较好的维护。另外在路网中的一些区域完全没有已知流量，可知已知流量的空间分布极不平衡。

2.2 变量

本研究以早晨7：00—8：00 车道小时交通量为因变量，以道路几何特征和建成环境特征为自变量。

在道路几何特征中，所有车道方向变量都是哑变量，其中直行方向为参考方向。其他道路几何特征包括路段长度、路段等级、下游道路等级、路段车道数量、公交线路数量、是否单行道、是否公交专用道、是否与快速路平行，以及上下游是否连接快速路。受数据条件的限制，建成环境特征包括车道附近的人口密度、平均房价、到最近三甲医院的距离、到最近购物中心的距离以及到最近大学的距离。变量选择使用MLR进行，统计上不显著以及方差膨胀因子（VIF）大于5.0 的变量［4-5］将被去掉。所有最终使用变量汇总见表1。

3 结果

3.1 扩样结果

使用第1.2 节中提出的扩样方法，将原始数据集从560车道扩大到2 217车道（整个路网）。如表1所示，扩样前后两个样本集的同一变量的均值和标准差相近。另外，一些变量，如车道数、公交线路数、人口密度和房价，在扩样后呈下降趋势。这是合理的，因为原始流量数据主要来自于较高等级道路的检测器，这些路段的变量，如车道数、公交线路数、人口密度等相对较大，当样本集扩大到整个路网时，即样本集中等级较低道路的比例增加时，这些自变量的均值随之减小［17］。

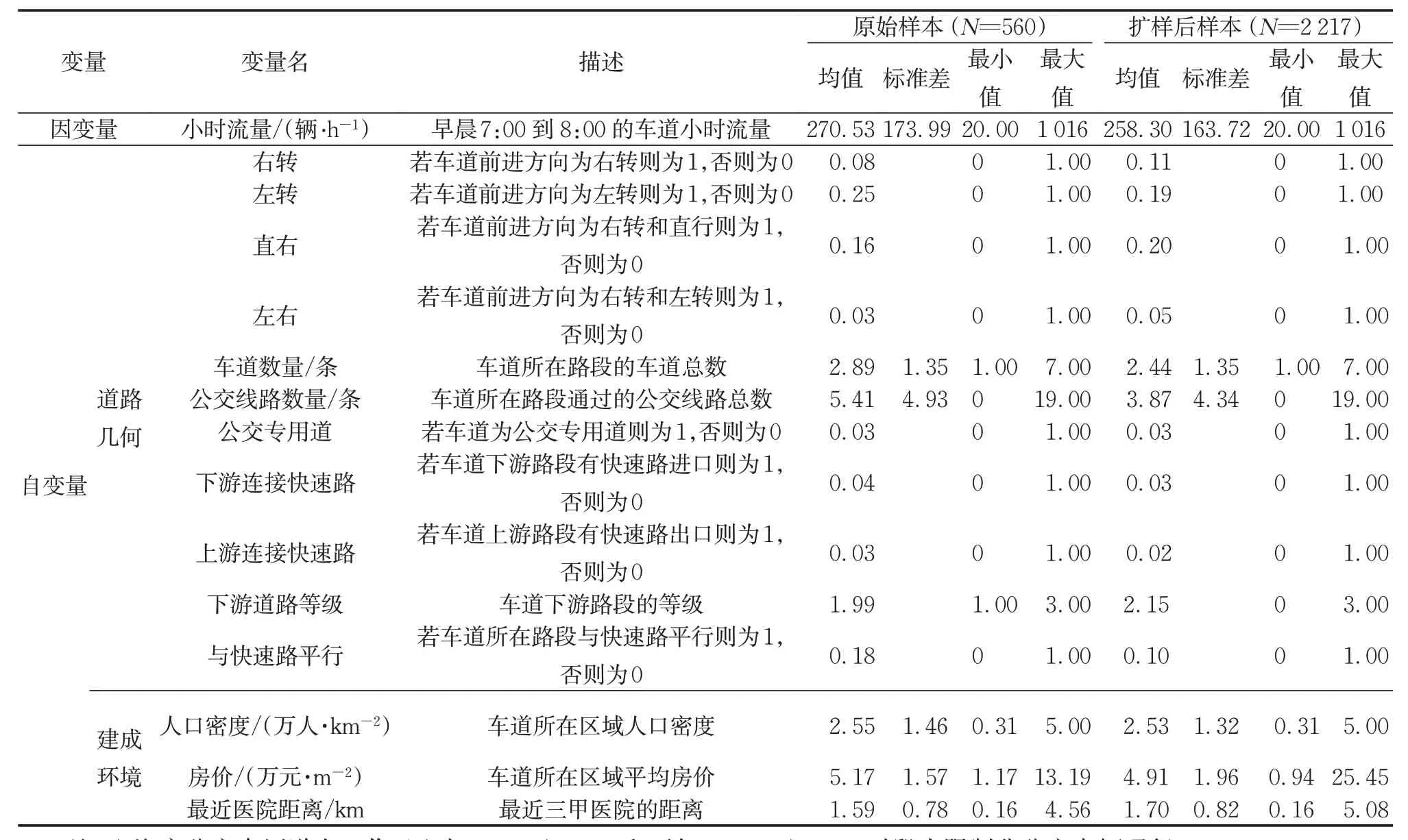
表1 自变量和因变量描述Tab.1 Description of dependent variables and independent variables

3.2 空间相关性检验

Moran’sI检验用于检验不同车道上小时交通量的空间相关性。原始样本的Moran’sI指数为0.055 6，P值为0.000 6。扩样后的样本，Moran’sI指数为0.147 4，P值为 0。Moran’sI检验表明车道小时交通流量之间存在显著的正空间相关性。也就是说，在空间上高流量车道与高流量车道聚集，低流量车道与低流量车道聚集。因此，利用空间模型来处理空间相关性是非常必要的。

3.3 回归结果

本研究分别对3 个模型进行了拟合和比较，它们分别是使用原始样本的MLR（模型1），使用原始样本的GWPR（模型2），和使用扩样后样本的GWPR（模型3），结果见表2。

对于模型1，所有方向相关变量与小时流量呈负相关（参考方向为直行）。其他变量，包括下游道路等级、路段车道数、最近医院距离、是否为公交专用道以及是否与快速路平行，也都与流量呈负相关。相反，公交线路数、附近的房价、附近的人口密度以及上下游是否连接快速路都呈现出正相关关系。

对于模型2和模型3，每条车道都有自己的回归系数。在表2中，系数由均值、最小值、最大值、正系数比例以及负系数比例来描述。如表2所示，3个模型中同一变量的系数（或系数均值）的符号相同，表明该变量对流量的整体影响在所有模型中一致。然而，当聚焦于局部区域时会观察到差异。模型3 在正系数比例和负系数比例中表现出最大的变化性，表明其捕捉自变量局部效应的能力最佳。与此相反，模型2 在很大程度上与模型1 一致，呈现较少的局部变化。如图2 所示，左图表示原始的已知车道小时流量，右图表示由模型3估计的车道小时流量，对比可知，估计的车道流量与已知的原始流量高度一致。

3.4 模型验证

为了比较模型的估计性能，本文进行了10倍的交叉验证，并采用了R平方值（R2）、均方根误差（RMSE）和绝对百分比平均误差（MAPE）3 种指标来衡量对验证结果。如表3所示，模型3的RMSE和MAPE 最小，并且R2最大。具体来说，与模型1 和模型2 相比，模型3 的RMSE 分别降低了11.4%和11.3%，MAPE 分别降低了16.3%和12.9%，R2分别提高了57.7%和33.5%。

表2 模型1、模型2和模型3的回归结果Tab.2 Regression results of model 1,model 2 and model 3

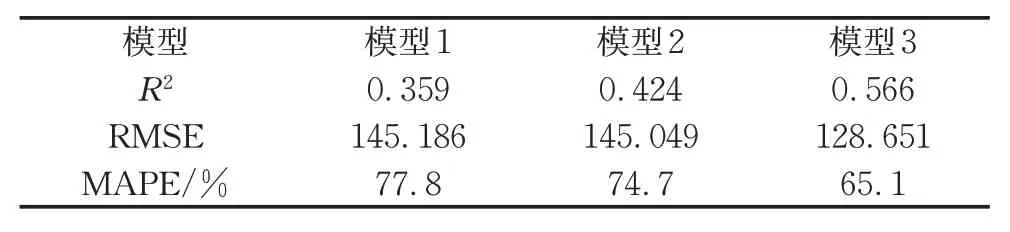
表3 模型1、模型2和模型3的交叉验证结果Tab.3 Cross validation results of model 1,model 2 and model 3

图2 已知车道交通量和估计车道交通量Fig.2 Known lane traffic volume and estimated lane traffic volume

综上所述，扩样技术和GWPR的联合使用不仅提高了模型的解释能力，而且提高了预测精度。值得注意的是，使用原始样本的GWPR 性能与MLR相近，即对于空间分布不均衡或大量缺失数据的样本而言，GWPR 本身并不会提高模型的性能。这也再次验证拟合模型前对不平衡的缺失数据的处理是有意义的。

4 讨论

除了高精度外，高解释性也是选择GWPR的原因。如表2 中所示，3 个模型的同一变量系数（或系数平均值）的符号一致。换言之，在不同的模型中，变量对交通量的全局影响的方向是一致的。然而，由于模型3 中各系数正负值所占比例的变化最大，因此采用扩样样本的GWPR 具有最大的空间异质性捕捉能力。在GWPR中，所有自变量的估计系数和P值在空间上都是不同的，这为解释自变量对流量的局部影响提供了更多的信息［13，16，23］。考虑到篇幅限制，本文只讨论几个信息量最大的自变量，包括右转、车道数、是否公交专用道、人口密度，共4个变量。如图3所示，在每个子图中，左图表示变量的系数值，点的大小随系数的增大而增大，正系数设为深灰色，负系数设为浅灰色；右图表示变量系数的显著性，统计上显著的系数（即P值＜0.1）设置为浅灰色，反之设置为深灰色。如图3所示，系数和系数显著性都在研究区域内呈现出变化趋势。

对于与车道方向变量，其中直行车道作为基本参考。右转变量与研究区域的交通量始终呈负相关，并且在大多数车道上统计显著（P值＜0.1）。左转变量与右转变量相似。表明右转和左转车道的交通量均低于直行车道，这是符合实际的，因为在大多数交叉口，直行车道流量都大于转弯车道流量。

在63%的车道中，路段车道数与交通量呈负相关，即路段车道数越多，每条车道的交通量越低。值得注意的是，这一结论似乎与一些现有研究不一致［5，10-11，16］。原因在于现有研究的因变量是路段交通量，而在本研究中是车道交通量。路段上的更多车道对应更大的交通量，但是在某一路段上，由于更多的车道共享路段交通量，每条车道的分享交通量反而会减少。此外，仍有37%的车道与交通量呈正相关，主要分布在研究区西南部。该区域靠近上海市中心，交通需求较大可能是导致与交通量正相关的主要原因。

另一个与交通量呈全局负相关的道路几何特征是公交专用道变量，表明公交专用道的设置显著降低了车道流量。人口密度与大多数车道（78%）的交通量呈正相关，这与之前的各种研究一致［4，12］。然而，仍有一些地方，人口密度呈负相关。其中一些在统计上不显著，而另一些主要位于主干道处。一种解释是，主干道上的大多数交通都是过境交通，这与当地社会人口结构（如人口密度）没有密切关系［19］。

图3 部分变量系数值与显著性的空间分布Fig.3 Spatial distribution of the values and significance of some variables

5 结论

本研究为观测值有限且分布不均时的交通流量估计提供了一种新的方法。首先用扩样技术填充不平衡缺失数据，然后用地理加权回归模型（GWPR）估计车道交通量。结果表明，与传统的MLR或直接使用GWPR相比，采样扩展技术和GWPR结合的方法具有更好的交通量估计性能。此外，GWPR 可以很好地捕捉自变量与交通量关系的空间异质性，为解释自变量的影响提供更多的细节。

值得进一步研究的是，首先，由于数据条件的限制，本研究未能包含足够的土地利用和社会人口特征，例如岗位密度和土地利用率等。这些因素都与交通量关系密切。若将它们纳入到模型中可以进一步提高模型拟合优度和精度。此外，大量新的数据源如手机数据、GPS数据等也在不断涌现，可以将这些新数据源与传统SCATS数据集成，以获得更高的流量估计性能。